Soluciones del apartado «Resuelve problemas»

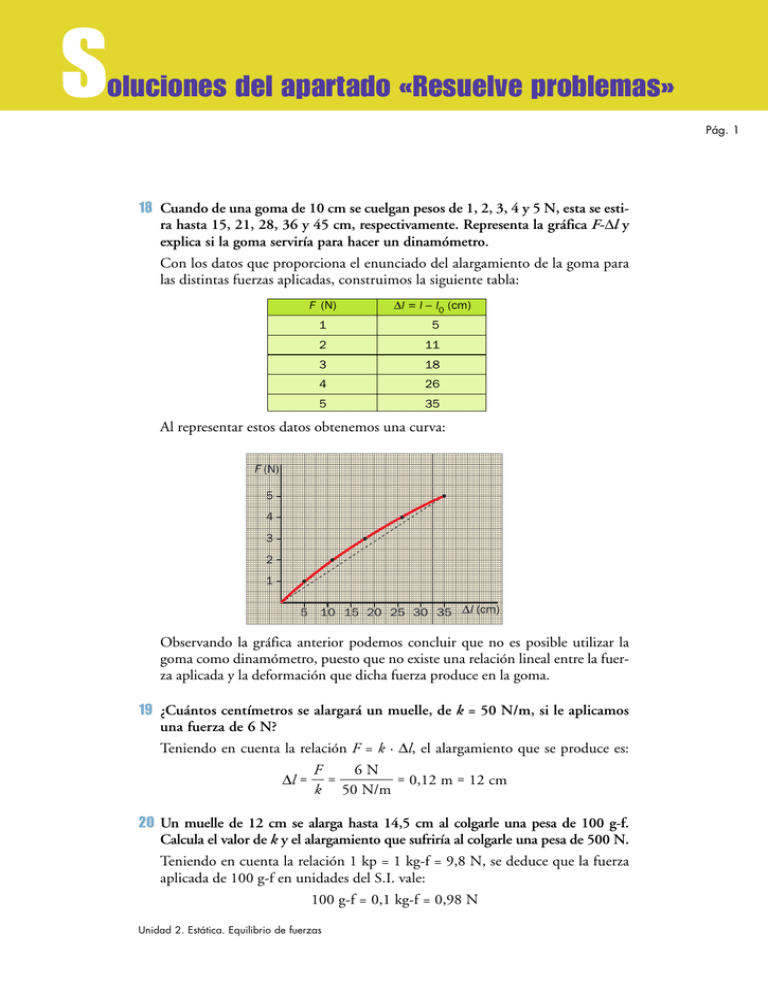
S
oluciones del apartado «Resuelve problemas»
Pág. 1
18 Cuando de una goma de 10 cm se cuelgan pesos de 1, 2, 3, 4 y 5 N, esta se estira hasta 15, 21, 28, 36 y 45 cm, respectivamente. Representa la gráfica F-Dl y
explica si la goma serviría para hacer un dinamómetro.
Con los datos que proporciona el enunciado del alargamiento de la goma para
las distintas fuerzas aplicadas, construimos la siguiente tabla:
F (N)
Dl = l – l0 (cm)
1
5
2
11
3
18
4
26
5
35
Al representar estos datos obtenemos una curva:
F (N)
5
4
3
2
1
5
10 15 20 25 30 35
Observando la gráfica anterior podemos concluir que no es posible utilizar la
goma como dinamómetro, puesto que no existe una relación lineal entre la fuerza aplicada y la deformación que dicha fuerza produce en la goma.
19 ¿Cuántos centímetros se alargará un muelle, de k = 50 N/m, si le aplicamos
una fuerza de 6 N?
Teniendo en cuenta la relación F = k · Dl, el alargamiento que se produce es:
6N
F
∆l = ᎏᎏ = ᎏᎏ = 0,12 m = 12 cm
k 50 N/m
20 Un muelle de 12 cm se alarga hasta 14,5 cm al colgarle una pesa de 100 g-f.
Calcula el valor de k y el alargamiento que sufriría al colgarle una pesa de 500 N.
Teniendo en cuenta la relación 1 kp = 1 kg-f = 9,8 N, se deduce que la fuerza
aplicada de 100 g-f en unidades del S.I. vale:
100 g-f = 0,1 kg-f = 0,98 N
Unidad 2. Estática. Equilibrio de fuerzas
S
oluciones del apartado «Resuelve problemas»
Pág. 2
Aplicando la ley de Hooke, F = k · Dl, podemos calcular la constante elástica
del muelle:
F
0,98 N
0,98 N
k = ᎏᎏ = ᎏᎏ = ᎏᎏ = 39,2 N/m
∆l 0,145 m – 0,12 m 0,025 m
Cuando la fuerza es de 500 N, el alargamiento que se produce en el muelle es:
F
500 N
∆l = ᎏᎏ = ᎏᎏ = 12,76 m
k 39,2 N/m
Teniendo en cuenta que es difícil imaginar un muelle de esta longitud, este resultado tan elevado nos hace suponer que al aplicar esta fuerza se superará el límite de elasticidad del muelle, con lo que la deformación producida será permanente.
21 Un dinamómetro tiene colgada una masa cuyo peso es de 3 N. Al añadir otra
de 1 N, el muelle se alarga 5 cm más respecto al alargamiento anterior.
Calcula k.
Puesto que en un dinamómetro existe una relación lineal entre la fuerza aplicada
y el alargamiento que se produce, no es necesario conocer el alargamiento que sufría el dinamómetro cuando colgaba de él el peso de 3 N; basta con saber que una
fuerza de 1 N produce un alargamiento de 5 cm. Aplicando la ley de Hooke:
F
1N
F = k · ∆l → k = ᎏᎏ = ᎏᎏ = 20 N/m
∆l 0,05 m
22 Un muelle tiene una longitud l0 = 15 cm. Al colgar una masa de 3 kg, se alarga 10 cm. Calcula el valor de k, la masa que debemos colgar del muelle para
que este se alargue 22 cm y el alargamiento que experimentará cuando se
cuelgue un peso de 35 N.
La constante elástica del muelle podemos obtenerla aplicando la ley de Hooke:
F 3 kg · 9,8 m/s2
F = k · ∆l → k = ᎏᎏ = ᎏᎏ = 294 N/m
0,1 m
∆l
Teniendo en cuenta la relación lineal que existe entre fuerza y alargamiento, la
masa colgada cuando el muelle se alarga 22 cm es:
F = P = k · ∆l = 294 N/m · 0,22 m = 64,68 N
P 64,68 N
m = ᎏᎏ = ᎏᎏ = 6,6 kg
g 9,8 N/kg
Cuando colguemos un peso de 35 N, el alargamiento del muelle será:
F
35 N
∆l = ᎏᎏ = ᎏᎏ = 0,12 m = 12 cm
k 294 N/m
Unidad 2. Estática. Equilibrio de fuerzas
S
oluciones del apartado «Resuelve problemas»
Pág. 3
23 El límite elástico de un muelle es 300 N, y k = 200 N/m:
a) Calcula el alargamiento que experimentará cuando colguemos de él una
masa de 10 kg.
b) Obtén el valor de la fuerza aplicada si Dl = 105 cm, y explica si perderá la
elasticidad por ello.
a) Cuando colgamos una masa de 10 kg, la fuerza que actúa sobre el muelle es:
F = m · g = 10 kg · 9,8 m/s2 = 98 N
Esta fuerza es menor que el límite de elasticidad del muelle, por lo que podemos aplicar la ley Hooke para calcular el alargamiento que se produce en este:
98 N
F
F = k · ∆l → ∆l = ᎏᎏ = ᎏᎏ = 0,49 m = 49 cm
k 200 N/m
b) Si el alargamiento es de 105 cm, la fuerza aplicada será:
F = k · ∆l = 200 N/m · 1,05 m = 210 N
Como vemos, este muelle tiene un límite de elasticidad muy elevado, por lo
que admite grandes deformaciones sin perder su comportamiento elástico.
24 Dos fuerzas iguales de 1 N que forman 90° se aplican sobre un objeto. Calcula el
módulo de la resultante y dibuja las tres fuerzas sobre unos ejes de coordenadas.
El módulo de la resultante, cuando las fuerzas se aplican formando un ángulo
de 90°, se obtiene aplicando el teorema de Pitágoras:
2 + 12 = 1,41 N
2
2
FR = 兹F
苶
苶
1 + F苶
2 = 兹1
FR = 1,41 N
Y
F2 = 1 N
α = 45°
F1 = 1 N
X
25 Calcula el valor y la dirección de la resultante del sistema de fuerzas. Dibuja
el esquema y la resultante en tu cuaderno.
5N
7N
15 N
4N
Unidad 2. Estática. Equilibrio de fuerzas
S
oluciones del apartado «Resuelve problemas»
Pág. 4
Restando las fuerzas opuestas, el sistema queda reducido a dos fuerzas perpendiculares de 8 N (hacia la derecha) y 1 N (hacia arriba), respectivamente.
El módulo de la resultante es:
2 + 12 =
R = 兹8苶
苶 = 8,1 N
兹65
Y
R
1N
Y su dirección y sentido se muestran en la figura de la derecha.
8N
X
26 Calcula el valor de las componentes rectangulares de una fuerza de 100 N que
forma 45° con el eje X.
La descomposición de la fuerza
en sus componentes rectangulares es:
Y
F = 100 N
Fy = 70,71 N
Fx = F · cos 45° =
= 100 N · 0,7071 = 70,71 N
Fy = F · sen 45° =
= 100 N · 0,7071 = 70,71 N
Fx = 70,71 N
X
27 Un caballo tira de una argolla, hacia el norte, con una fuerza de 2000 N, y
otro hacia el este, con 3000 N. ¿Con qué fuerza ha de tirar un tercer caballo
y hacia dónde para que la argolla quede en equilibrio?
La resultante de las fuerzas que aplican los dos caballos es:
FR = 兹苶
3 0002苶
+ 2 00苶
02 = 3 605,55 N
Para que la argolla quede en equilibrio, el tercer caballo ha de tirar con una
fuerza del mismo valor que la resultante que acabamos de hallar, pero en sentido opuesto:
FR = 3605,55 N
2000 N
3000 N
–FR = 3605,55 N
Unidad 2. Estática. Equilibrio de fuerzas
S
oluciones del apartado «Resuelve problemas»
Pág. 5
28 Dos fuerzas de 50 y 70 N están dirigidas una hacia el norte y otra hacia el
este. Calcula la resultante y el ángulo que forma con la dirección oeste-este.
La resultante de las dos fuerzas es:
2 + 702 = 86,02 N
FR = 兹50
苶
苶
y el ángulo que forma esta fuerza con la línea oeste-este es:
50
tg α = ᎏᎏ = 0,7143 → α = arctg 0,7143 = 35,54° = 35° 32’
70
FR = 86,02 N
50 N
70 N
29 ¿Estará en equilibrio un sistema formado por tres fuerzas que forman ángulos de 120°, dos de las cuales son de 100 N y la tercera de 50 N? ¿Y el de la
figura?
60 N
67,08 N
90°
30 N
El primer sistema propuesto en el enunciado no estará en equilibrio puesto
que, al ser iguales los ángulos pero distintos los valores de las fuerzas, la resultante de dos cualesquiera de ellas no es igual a la tercera.
Para calcular la resultante del sistema, debemos elegir cuidadosamente el sistema de referencia en el que situar las fuerzas. Si colocamos el eje X en la dirección de la fuerza de 50 N, las dos fuerzas de 100 N se encontrarán en el segundo y en el tercer cuadrante, respectivamente, formando ángulos de 60° con el
eje X y de 30° con el eje Y.
La resultante de las dos fuerzas de 100 N la obtenemos calculando sus componentes rectangulares:
F1x = 100 N · cos 60° = 50 N
F1y = 100 N · sen 60° = 86,6 N
Unidad 2. Estática. Equilibrio de fuerzas
S
oluciones del apartado «Resuelve problemas»
Pág. 6
F2x = 100 N · cos 60° = 50 N
F2y = 100 N · sen 60° = 86,6 N
Al sumar estas fuerzas, componente a
componente, debemos tener en cuenta
que las componentes en el eje X tienen
el mismo sentido, por lo que deben sumarse, mientras que las componentes
en el eje Y tienen sentidos opuestos y
deben restarse:
Y
F1 = 100 N
F1y
30°
60°
F = F1 + F2
F1x = F2x
F3 = 50 N
X
60°
30°
Fx = F1x + F2x = 50 N + 50 N = 100 N
Fy = F1y –F2y = 86,6 N – 86,6 N = 0
F2 = 100 N
F2y
Por tanto, la suma de estas dos fuerzas es otra fuerza de 100 N en la dirección
del eje X y en sentido opuesto a la de 50 N. Si calculamos ahora la resultante de
estas dos, obtenemos:
FR = F – F3 = 100 N – 50 N = 50 N
En cuanto al segundo sistema, el propuesto en la figura, para determinar si está
en equilibrio debemos calcular la resultante de las tres fuerzas. La resultante de
las fuerzas de 60 y 30 N es:
2 + 602 = 67,08 N
FR = 兹30
苶
苶
Su dirección es la diagonal del paralelogramo, y su sentido, hacia la derecha.
Por tanto, el sistema se reduce a dos fuerzas del mismo valor aplicadas en sentidos opuestos, por lo que su resultante es nula, lo que quiere decir que el sistema
se encuentra en equilibrio.
30 Calcula el valor de A para que el sistema esté en equilibrio; primero, suponiendo el peso de la barra despreciable y, después, considerando que esta pesa
2 N.
20 cm
A
15 cm
10 cm
4N
10 cm
50 N
a) Suponiendo el peso de la barra despreciable (con las fuerzas expresadas en N
y las distancias en cm):
A · 20 cm + 4 N · 15 cm = 50 N · 10 cm
Unidad 2. Estática. Equilibrio de fuerzas
8 A = 440 = 22 N
20
S
oluciones del apartado «Resuelve problemas»
Pág. 7
NOTA: Para ofrecer otras posibilidades, resolvemos aquí el segundo apartado de este problema
de modo diferente a como se hace en la Propuesta Didáctica.
b) La barra pesa 2 N. Su longitud es de 55 cm, de los que 35 cm (el 63,7%) están a la izquierda del punto de apoyo y 20 cm (el 36,3%) a la derecha. Supuesta homogénea, a la derecha descansarían:
2 N · 63,7/100 = 1,27 N
que podemos suponer en el centro de gravedad de esta porción de la barra,
situado 17,5 cm a la izquierda del fulcro. La parte derecha tendría un peso:
2 N · 36,3/100 = 0,73 N
situado 10 cm a la derecha del punto de apoyo.
Con esto:
A · 20 cm + 4 N · 15 cm + 1,27 N · 17,5 cm= 50 N · 10 cm + 0,73 N · 10 cm
A = 425,1 = 21,25 N
20
31 Para abrir una puerta, tenemos que ejercer una fuerza de 2 N a 40 cm de las
bisagras. Averigua si aplicando una fuerza de 3 N a 20 cm se abrirá o no la
puerta.
El momento de la fuerza es:
M1 = F · d = 2 N · 0,4 m = 0,8 m · N
Para saber si aplicando la fuerza de 3 N a 20 cm de las bisagras conseguiremos
abrir la puerta, debemos comparar el momento de esta fuerza con el calculado
anteriormente:
M2 = 3 N · 0,2 m = 0,6 m · N 8 M2 < M1
Esto nos indica que no se abrirá la puerta.
32 Para girar el timón de una embarcación, necesitamos aplicar un momento de
3 N · m. Si el diámetro del timón es de 30 cm, calcula el valor de las fuerzas
que se han aplicado y el del momento de cada una de ellas.
a) De la expresión que proporciona el momento del par de fuerzas despejamos
el valor de dichas fuerzas:
M 3m·N
M = F · d 8 F = ᎏᎏ = ᎏᎏ = 10 N
d
0,3 m
En esta expresión, d es el diámetro del timón.
a) El momento de cada una de ellas es:
M1 = M2 = F · d = 10 N · 0,15 m = 1,5 m · N
Unidad 2. Estática. Equilibrio de fuerzas
S
oluciones del apartado «Resuelve problemas»
Pág. 8
Ahora, d representa el radio del timón (distancia del eje de giro a la fuerza).
Como vemos, la suma de los momentos es igual al momento del par:
M = M1 + M2 = 1,5 m · N + 1,5 m · N = 3 m · N
33 Queremos transportar un cuerpo en una carretilla. ¿En qué posición hemos
de colocarlo para transportarlo con menor esfuerzo, en la parte delantera cercana a la rueda, en el centro o en la posterior? Razónalo.
Debemos transportar el objeto en la parte delantera porque, al disminuir la
distancia de la fuerza resistente al punto de apoyo (la rueda), disminuye el momento que tenemos que vencer.
34 El cubo con el que se saca agua de un pozo pesa 16 kp lleno. Si utilizamos un
torno cuyo cilindro mide 5 cm de radio, calcula la longitud que debe tener el
mango para que podamos subir el cubo con una fuerza de 4 kp.
En el torno, los momentos ejercidos en el mango y en el cilindro han de ser
iguales. Por tanto, el mango debe medir:
F · rF = P · rP 8 16 kp · 0,05 m = 4 kp · rP 8 rP = 0,2 m = 20 cm
35 Con un polipasto de tres poleas móviles se levanta un saco de 76 kg-f de peso.
¿Qué fuerza se ha ejercido?
Con tres poleas móviles, la fuerza a aplicar será 23 = 8 veces menor que la fuerza que debemos vencer; esto es:
F = 76 kp = 9,5 kp
8
Unidad 2. Estática. Equilibrio de fuerzas