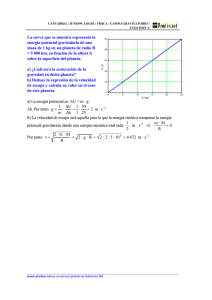
Justificación de la expresión matemática de la Ley de Gravitación

Justificación de la expresión matemática de la Ley de Gravitación Universal
Newton expuso su Ley basándose en los siguientes hechos derivados de las Leyes de Kepler:
1.- Los planetas y satélites se mueven sin seguir un movimiento rectilíneo y uniforme por lo que debe existir una fuerza no nula que
actúe sobre ellos.
2.- En virtud de la 2ª Ley de Kepler la mencionada fuerza debe ser continuamente central para que se mantenga constante la
velocidad aerolar.
dA 
r  ds r 2  d

2
2
ds  r  d




L  r x p  L  r  m  v  sen  r  m  v

L  r m
ds
r  d
d
dA
 r m
 mr2 
 2m
dt
dt
dt
dt
 L  2m
dA
Como la velocidad areolar debe
dt
ser constante según la 2ª ley de Kepler el momento angular también lo será.

Además la dirección de L también debe ser constante para que el movimiento del planeta este localizado siempre en el mismo
plano. También el sentido de rotación en el movimiento de traslación debe ser constante para que el planeta gire siempre en el
mismo sentido.
Por tanto el momento angular de los planetas que giran alrededor debe ser constante.


 
dL
M 
 0 Si M  0  r  F  0
dt

Esto sólo puede ocurrir en dos casos:

Si la F  0 (Esto está en contra del primer argumento)
a)

b) Si la
F
es central.
Por esto Newton dedujo que la fuerza que provoca el movimiento de los planetas alrededor del Sol es de tipo central. (Esto también
se le puede aplicar al movimiento de un satélite, natural o no, alrededor de un planeta)
3.- La fuerza que provoca un movimiento cónico (círculos, elíptico, parabólico o hiperbólico) es inversamente proporcional al
cuadrado de la distancia entre el cuerpo y el foco de la cónica.


F  m p ac  m p 
v2
4 2
T2
 m p   2  r  m p  2  r y aceptando la tercera ley de Kepler 3  K  T 2  K  r 3
r
r
T
obtenemos:
mp
4 2  r 4 2 m p
Fp  m p 



C
p
K r2
K  r3
r2
Esta F es proporcional a la masa del planeta , teniendo en cuenta la 3ª Ley de Newton en el Sol habrá otra fuerza que debe ser igual
en dirección y módulo pero de distinto sentido que será por tanto proporcional a la masa del Sol.
Fs  C s 
Ms
r2
por tanto
Fs  Fp
 Cp
mp
r2
 Cs
Cp
Ms
C

C

m

C

M

 s G
p
p
s
s
2
Ms mp
r
donde G representa no sólo una constante de proporcionalidad sino una constante universal, común a todos los planetas (como la K
de la 3ª Ley de Kepler ) y también válida para el propio Sol.
Fp  C p
mp
Fs  C s
Ms
r2
r2
como
C p  G  M s  Fp  G
como
C s  G  m p  Fs  G
Ms  mp
r2
Ms  mp
r2
Es lógico pensar que el responsable de la fuerza que sufre cada planeta es el Sol, porque este se encuentra en el foco de todas las
elipses planetarias.
4.- La fuerza que sufre cada planeta representa una faceta de la fuerza mutua de interacción con el Sol, de tal forma que entre el Sol
y cada planeta aparece una fuerza de atracción. Y este par de fuerzas de acción y reacción tiene origen en el hecho de que el Sol y el
planeta poseen masas que se perciben mutuamente, originando una fuerza de interacción gravitatoria similar a la que existe entre un
cuerpo que cae y la Tierra.
La interacción gravitatoria entre dos cuerpos puede expresarse por una fuerza de atracción central, proporcional a las masas de los
cuerpos e inversamente proporcional al cuadrado de la distancia que las separan.
Debido a esto ya no es necesario separar el movimiento de los cuerpos celestes del movimiento de caída libre en la Tierra. La fuerza
que provoca ambos movimientos es la misma. (Síntesis Newtoniana).
Por tanto, podemos decir que la Luna está cayendo hacia la Tierra como consecuencia de la atracción que la Luna sufre. Esta fuerza
es análoga al peso del cuerpo pero con una gravedad mucho menor ya que la Luna se encuentra muy alejada de la superficie
terrestre donde la gravedad g  9'8 m
s2
(La gravedad que sufre la Luna por la acción de la Tierra es 2,72  10
3
m
s2
). Lo que
ocurre es que no termina nunca de llegar al suelo porque está animada con una velocidad horizontal (tangente a la trayectoria casi
circular que describe) que la empuja siempre más allá de la vertical, lo suficiente para que nunca “caiga”. Si no fuera por esa
velocidad horizontal se caería verticalmente al igual que lo hace una manzana despedida del árbol, salvo con aceleración creciente
hacia el valor de g  9'8 m
s2
que es el que tendría al llegar a la superficie terrestre.
Supongamos que hacemos llegar un cuerpo a una altura h sobre la superficie terrestre. En ese punto le damos una velocidad
v o perpendicular a la vertical. Dependiendo del valor de la velocidad, el cuerpo descubrirá las distintas trayectorias que se
describen.
o Si la v0  0
el cuerpo caerá sobre la vertical del lugar.
o Si la v o no es lo suficiente el cuerpo caerá sobre la tierra describiendo un movimiento llamado tiro horizontal.
o Si la v o está entre unos valores el cuerpo describirá una trayectoria elíptica alrededor de la Tierra (Se pondrá en órbita).
o Si la v o es lo suficientemente grande el cuerpo “escapará” de la atracción gravitatoria describiendo una parábola o una
hipérbola.