Pérdidas magnéticas por efecto de histéresis

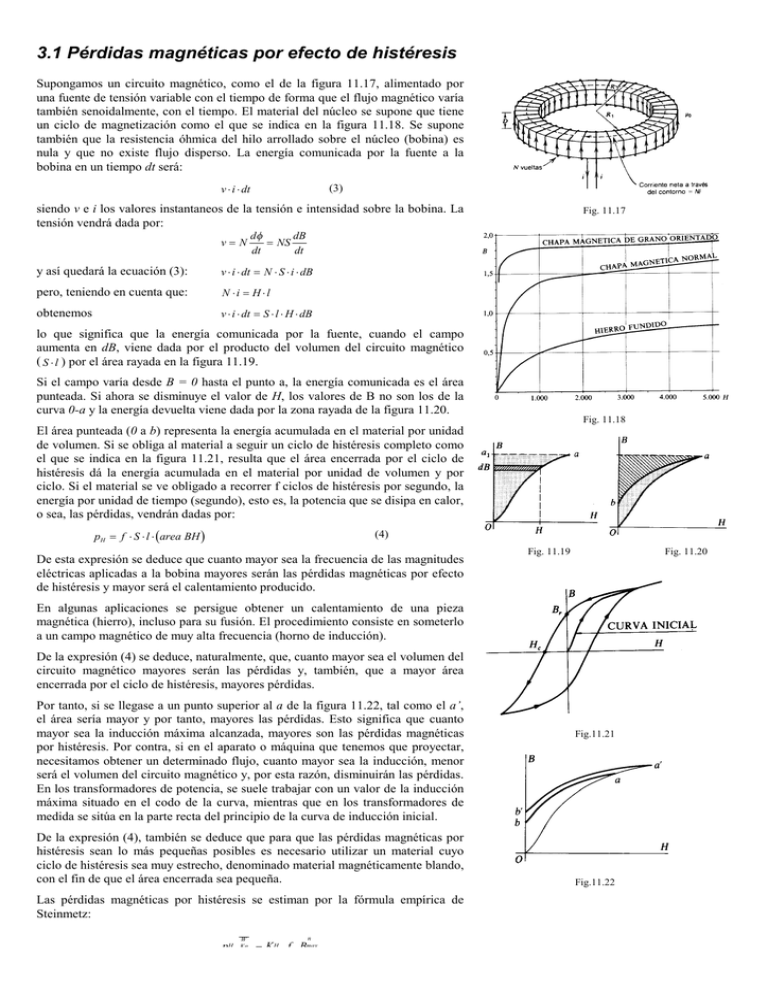
3.1 Pérdidas magnéticas por efecto de histéresis
Supongamos un circuito magnético, como el de la figura 11.17, alimentado por
una fuente de tensión variable con el tiempo de forma que el flujo magnético varía
también senoidalmente, con el tiempo. El material del núcleo se supone que tiene
un ciclo de magnetización como el que se indica en la figura 11.18. Se supone
también que la resistencia óhmica del hilo arrollado sobre el núcleo (bobina) es
nula y que no existe flujo disperso. La energía comunicada por la fuente a la
bobina en un tiempo dt será:
v ⋅ i ⋅ dt
(3)
siendo v e i los valores instantaneos de la tensión e intensidad sobre la bobina. La
tensión vendrá dada por:
v=N
Fig. 11.17
dB
dφ
= NS
dt
dt
y así quedará la ecuación (3):
v ⋅ i ⋅ dt = N ⋅ S ⋅ i ⋅ dB
pero, teniendo en cuenta que:
N ⋅i = H ⋅l
obtenemos
v ⋅ i ⋅ dt = S ⋅ l ⋅ H ⋅ dB
lo que significa que la energía comunicada por la fuente, cuando el campo
aumenta en dB, viene dada por el producto del volumen del circuito magnético
( S ⋅ l ) por el área rayada en la figura 11.19.
Si el campo varía desde B = 0 hasta el punto a, la energía comunicada es el área
punteada. Si ahora se disminuye el valor de H, los valores de B no son los de la
curva 0-a y la energía devuelta viene dada por la zona rayada de la figura 11.20.
Fig. 11.18
El área punteada (0 a b) representa la energía acumulada en el material por unidad
de volumen. Si se obliga al material a seguir un ciclo de histéresis completo como
el que se indica en la figura 11.21, resulta que el área encerrada por el ciclo de
histéresis dá la energía acumulada en el material por unidad de volumen y por
ciclo. Si el material se ve obligado a recorrer f ciclos de histéresis por segundo, la
energía por unidad de tiempo (segundo), esto es, la potencia que se disipa en calor,
o sea, las pérdidas, vendrán dadas por:
pH = f ⋅ S ⋅ l ⋅ (area BH )
(4)
De esta expresión se deduce que cuanto mayor sea la frecuencia de las magnitudes
eléctricas aplicadas a la bobina mayores serán las pérdidas magnéticas por efecto
de histéresis y mayor será el calentamiento producido.
Fig. 11.19
Fig. 11.20
En algunas aplicaciones se persigue obtener un calentamiento de una pieza
magnética (hierro), incluso para su fusión. El procedimiento consiste en someterlo
a un campo magnético de muy alta frecuencia (horno de inducción).
De la expresión (4) se deduce, naturalmente, que, cuanto mayor sea el volumen del
circuito magnético mayores serán las pérdidas y, también, que a mayor área
encerrada por el ciclo de histéresis, mayores pérdidas.
Por tanto, si se llegase a un punto superior al a de la figura 11.22, tal como el a’,
el área sería mayor y por tanto, mayores las pérdidas. Esto significa que cuanto
mayor sea la inducción máxima alcanzada, mayores son las pérdidas magnéticas
por histéresis. Por contra, si en el aparato o máquina que tenemos que proyectar,
necesitamos obtener un determinado flujo, cuanto mayor sea la inducción, menor
será el volumen del circuito magnético y, por esta razón, disminuirán las pérdidas.
En los transformadores de potencia, se suele trabajar con un valor de la inducción
máxima situado en el codo de la curva, mientras que en los transformadores de
medida se sitúa en la parte recta del principio de la curva de inducción inicial.
De la expresión (4), también se deduce que para que las pérdidas magnéticas por
histéresis sean lo más pequeñas posibles es necesario utilizar un material cuyo
ciclo de histéresis sea muy estrecho, denominado material magnéticamente blando,
con el fin de que el área encerrada sea pequeña.
Las pérdidas magnéticas por histéresis se estiman por la fórmula empírica de
Steinmetz:
pH
W
Kg
n
= K H f Bmax
Fig.11.21
Fig.11.22
KH es una constante que depende del tipo de chapa magnética y que es proporcionada por el fabricante de la misma, f es la frecuencia,
Bmáx es la inducción máxima y n un número comprendido entre 1.5 y 2.3. Las pérdidas se expresan en vatios por unidad de peso (Kg.)
de la chapa utilizada.