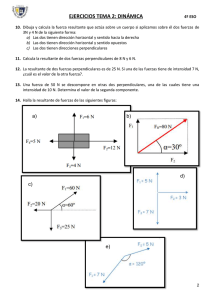
1.- Determinar la magnitud de la fuerza resultante así como su

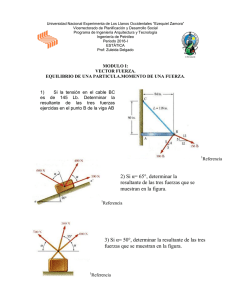
1.- Determinar la magnitud de la fuerza
resultante así como su dirección.
Sol.
Sol. R  546 N
,   253
2.- Tres fuerzas actúan en O, como se muestra
en la figura. Determinar la magnitud y
dirección de la resultante.
Sol. F2  228.2 lb ,   150.34
3.a) Si se sabe que α=40◦, determinar la
resultante de las tres fuerzas mostradas.
b) Determinar el valor requerido de α si la
resultante de las tres fuerzas mostradas
debe ser paralela al plano inclinado y la
magnitud correspondiente de la resultante.
a  R  203 lb ,   8.46
b   56.3 , R  204 lb
4.- Se aplican dos fuerzas en el gancho de apoyo
mostrado. Sabiendo que la magnitud de P es de
600 N, determinar el ángulo α requerido si la
resultante de las dos fuerzas aplicadas en el
gancho es vertical y la correspondiente magnitud
de dicha resultante.
Sol.   72.2 ,
R  1.391 kN
5.- La resultante de las dos fuerzas tiene una
magnitud de 650 lb. Determinar la dirección de
la resultante y la magnitud de P.
Sol.   71.8 ,
P  235 lb
6.- Si la resultante de las fuerzas A y B tiene
una magnitud de 1000 lb y la magnitud de la
fuerza A también es de 1000 lb, determinar el
valor del án gulo θ y de la fuerza B.
Sol. F AB  202.32 N
Sol.   90 , B  1414 lb
,
FCB  418.28 N
9.- La componente x de la fuerza P es 140 N
hacia la izquierda. Calcular P.
7.- Los cables A , B y C ayudan a soportar una
columna de una estructura. Las magnitudes de
las fuerzas ejercidas por los cables son ig uales:
F A =F B =F C. La magnitud de la suma vectorial de
las 3 fuerzas es de 200 kN. ¿Qué valor tiene F A ?
Sol. P  161.2 N
10.- Descomponer la fuerza F 1 y F 2 en
componentes que actúen a lo largo de los ejes u y
v , y determinar las magnitudes de sus
componentes.
Sol. FA  68.2 kN
8.- Calcular las componentes de la fuerza de 250
N que actúan a lo largo de las dos barras AB y
CB.
Sol.
F1u  183 N , F1v  129 N
F2 u  150 N , F2v  77.6 N
;