SOLUCIÓN

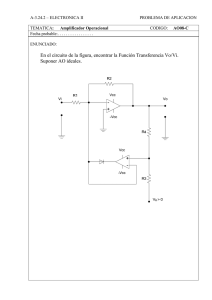
Electrónica Analógica (305-010-303)
Septiembre 2010
Universidad de Vigo
APELLIDOS Y NOMBRE:
SOLUCIÓN
DNI:
-----------------------------------------------------------------------------------------------------------------------1) El circuito de la figura representa una red RC de desplazamiento de fase, cuya función
de transferencia se indica.
R1 = R2 = R3 = R = 10 k
C1 = C2 = C3 = C = 6,5 nF
V1 es la señal aplicada a la entrada
V2 es la señal medida en la salida
V2
ω 3 R 3C 3
= 3 3 3
V1 ω R C − 5ωRC + j 1 − 6ω 2 R 2 C 2
(
)
Se desa realizar un oscilador senoidal basado en la red de realimentación dada. Se pide:
a) Determinar la frecuencia a la que es posible obtener la oscilación (1 punto).
La oscilación se produce a una frecuencia tal que anule la parte imaginaria de V2/V1 :
1 − 6ω 2 R 2 C 2 = 0
fo =
1
2π 6 RC
6ω 2 R 2 C 2 = 1
ω2 =
1
6R 2 C 2
= 999,61Hz
b) Diseñar el circuito del oscilador senoidal completo empleando un amplificador operacional ideal,
la red RC dada, y los mínimos componentes pasivos adicionales necesarios. Se permite realizar
modificaciones menores en la red RC, si se considera
conveniente. (2 puntos).
R3 se conecta a tierra virtual (V- del operacional) en
vez de conectarse a tierra real. La red mantiene su
comportamiento porque ambos puntos tienen tensión
cero.
Al mismo tiempo, R3, R4 y el operacional forman un
amplificador inversor de ganancia:
Av = -R4 / R3 = R4 / 10k
Para f = fo, se tiene:
3
3
3
2
2
2
1
6
ωRC
ω RC
V2
1
= 3 3 3
= 2 2 2
=
=−
1
29
V1 ω R C − 5ωRC ω R C − 5
−5
6
La ganancia de bucle ha de ser uno, por lo tanto se requiere una ganancia –29 en el
amplificador.
-29 = -R4 / 10k
R4= 290k
2) El amplificador operacional del circuito de la
figura se puede considerar ideal, excepto por tener
la tensión de salida limitada a los valores de
alimentación. El comportamiento de los diodos
queda definido por las siguientes expresiones:
VD < 0,6 V → ID= 0
ID > 0 → VD= 0,6 V
a) (2,5 puntos) Determinar las tensiones Va,
Vb y Vc en función de Ve, para valores de Ve
en el intervalo –3V < Ve < 3 V.
Representarlas con las acotaciones oportunas.
Va
4,4V
Mientras el operacional no se satura, V- = 0
pendiente =-2
Para Ve > 0) D1 OFF ; D2 ON
-2,2V
5V
Ve
Vb
Vb está a –0,6V , y por lo tanto el operacional son se satura.
0,6V
Para Ve < 0) D1 ON ; D2 OFF
Ve
-0,6V
Vc
Ve
-0,533
Mientras no se satura, V- = 0
Va = −Ve
R2
= −2 ⋅Ve
R1
Vb = −2 ⋅ Ve + 0,6
Vc = 0
Se satura si Vb es mayor o igual a 5V.
5 = −2 ⋅ Ve + 0,6
2 ⋅Ve = −4,4
Ve = −2,2
I=
(4,4 − Ve ) = ( 4,4 − Ve)
R1 + R 2
15k
En la zona de saturación, se tiene
Vc = Ve +
4,4 − Ve
 1
⋅ 5 = Ve ⋅ 1 −  + 1,467
15
 3
Vc = 0,667 ⋅ Ve + 1,467
b) (1 punto) Indicar de forma razonada cuál es la función que realiza este circuito y para que
margen de tensiones de entrada funciona correctamente.
Es un rectificador de media onda inversor (rápido, etc), con entrada en Ve y salida en Va.
Funciona correctamente con tensiones de entrada Ve desde -2,2 V hasta infinito
(teóricamente).
3) El circuito de la figura utiliza dos
operacionales que se pueden considerar
ideales excepto por tener sus tensiones de
salida limitadas al margen definido por las
tensiones de alimentación (± Vcc = ± 10 V).
a) Obtener la expresión analítica de vo en
función de v1 y representarla gráficamente,
realizando las acotaciones oportunas. (1,5
puntos)
OP2 está configurado como comparador de
Schmitt no inversor.
Vo
Si llamamos Vx a la tensión en la entrada inversora de
OP2, y Vy a la de la entrada no inversora:
Vx = 10 ⋅
10V
12
= 4V
18 + 12
El comparador
conmuta a +Vcc
cuando Vy supera
a Vx.
V1
-10V
Vy = 4V
2,5V
I=
4 + 10
= 0,35mA
40k
V 1 = 3,5 + 4 = 7,5V
El comparador conmuta a -Vcc cuando:
I=
6
= 0,15mA
40k
V 1 = 4 − I ⋅ R1 = 2,5V
Se dibuja la función de transferencia típica del comparador de Schmitt.
7,5V
b) Determinar la señal presente en v1, cuando se aplica en vi la señal dada. Representarla
gráficamente realizando las acotaciones oportunas. Datos:
duración del impulso= t1= 30 µs. El condensador se supone
vi
descargado en t= 0. (1 punto)
0
t1
0V
El OP1 está configurado como integrador inversor.
V1 = −
-3V
v1
1
Vi ⋅ dt
R0 ⋅ C1 ∫
9V
t
En el intervalo de tiempo de 0 a t1, Vi es constante e igual a
–3V, y la integral se resuelve:
V1 =
t
7,5V
3V
t
10µs
vo
Para t = 30 µs se tiene:
10V
V1 = 9V
Por lo tanto, V1 crece desde 0 hasta 9V con pendiente
constante en el intervalo de tiempo de 0 a t1.
t
-10V
A partir de t1, V1 se mantiene constante (9V) puesto que Vi se hace cero.
Se dibuja la gráfica de V1.
c) Determinar la señal presente en vo para las mismas condiciones del apartado b. Representarla
gráficamente realizando las acotaciones oportunas. (1 punto)
Vo se mantiene a –10V, y no conmuta hasta que V1 alcance el valor 7,5V.
Los 7,5V se alcanzan para t = (7,5 / 9) · 30 = 25 µs.
Se dibuja la gráfica de Vo.
Las siguientes SIMULACIONES se dan solamente como información complementaria.
Simulación aproximada del ejercicio 1:
Se simula con R4 = 310k para forzar un arranque más rápido
Gráfica que muestra el arranque de la oscilación en Vo:
Gráfica que muestra la estabilización de la amplitud en Vo (saturación del operacional):
Simulación aproximada del ejercicio 2:
Ve en el eje horizontal, de –3 a +3 V.
Va es cero para Ve > 0 (ese trazo queda tapado por Vc).
Va sube hasta aproximadamente 4,4 V para Ve = -3V.
Vb es máximo (5V aprox) para Ve = -3V.
Vb es mínima (-0,56 V aprox) para Ve = 3V.
Vc se mantiene a cero mientras el operacional no se satura.
Vc baja hasta aproximadamente – 0,53 V para Ve = -3V cuando se satura.
La simulación emplea modelos más cercanos a la realidad que los empleados en el cálculo manual
(lineales a tramos), por lo que en estas gráficas aparecen tramos curvos que suavizan el trazado.
Simulación aproximada del ejercicio 3:
Vin de la gráfica equivale a Vi del ejercicio (impulso negativo de 3V).
V1 crece desde cero hasta 9V, y se mantiene en este valor.
Vo conmuta de –Vcc a +Vcc en t = 25 us aproximadamente (V1 = 7,5V).