Para iniciar, considere una placa plana horizontal

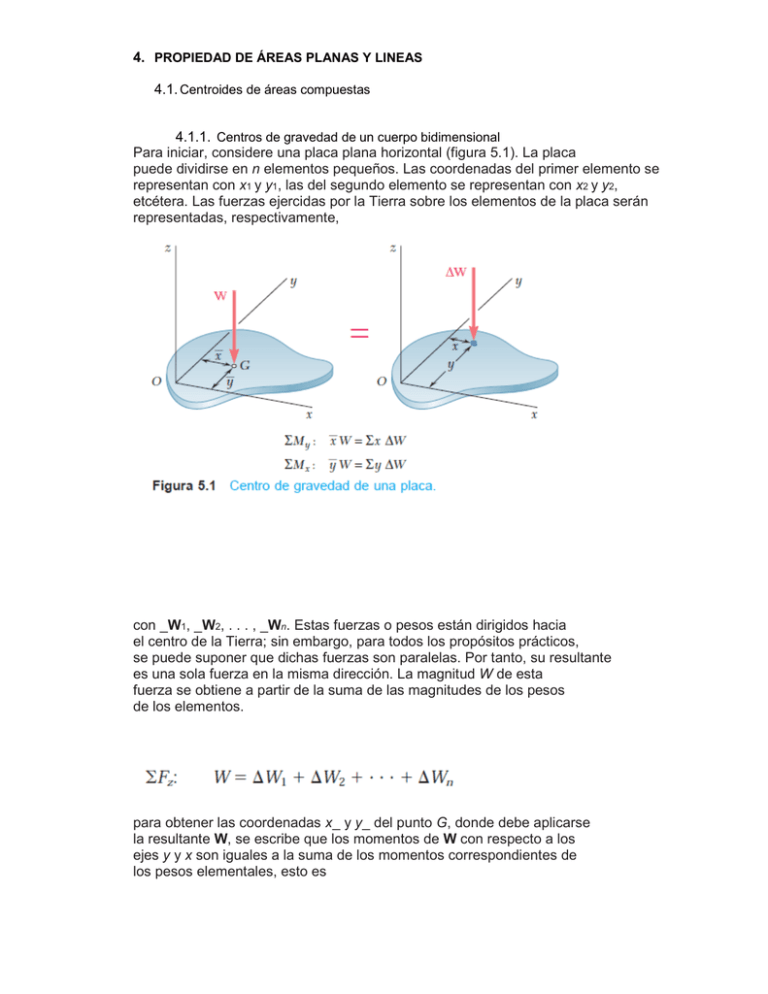
4. PROPIEDAD DE ÁREAS PLANAS Y LINEAS
4.1. Centroides de áreas compuestas
4.1.1. Centros de gravedad de un cuerpo bidimensional
Para iniciar, considere una placa plana horizontal (figura 5.1). La placa
puede dividirse en n elementos pequeños. Las coordenadas del primer elemento se
representan con x1 y y1, las del segundo elemento se representan con x2 y y2,
etcétera. Las fuerzas ejercidas por la Tierra sobre los elementos de la placa serán
representadas, respectivamente,
con _W1, _W2, . . . , _Wn. Estas fuerzas o pesos están dirigidos hacia
el centro de la Tierra; sin embargo, para todos los propósitos prácticos,
se puede suponer que dichas fuerzas son paralelas. Por tanto, su resultante
es una sola fuerza en la misma dirección. La magnitud W de esta
fuerza se obtiene a partir de la suma de las magnitudes de los pesos
de los elementos.
para obtener las coordenadas x_ y y_ del punto G, donde debe aplicarse
la resultante W, se escribe que los momentos de W con respecto a los
ejes y y x son iguales a la suma de los momentos correspondientes de
los pesos elementales, esto es
Si ahora se incrementa el número de elementos en los cuales se ha dividido la placa
y simultáneamente se disminuye el tamaño de cada elemento se obtienen, en el
límite, las siguientes expresiones:
Estas ecuaciones definen el peso W y las coordenadas x_ y y_ del centro
de gravedad G de una placa plana. Se pueden derivar las mismas ecuaciones
para un alambre que se encuentra en el plano xy (figura 5.2).
Se observa que usualmente el centro de gravedad G de un alambre no
está localizado sobre este último.
4.1.2. Centros de gravedad de áreas y líneas
En el caso de una placa plana homogénea de espesor uniforme, la magnitud
ʌW del pcso de un elemento de la placa puede expresarse como
En forma similar, se puede expresar la magnitud W del peso de toda
la placa como
donde A es el área total de la placa.
Si se emplean las unidades de uso común en Estados Unidos, se debe expresar el
peso específıco µen lb/ft3, el espesor t en pies y las áreas A y A en pies
cuadrados. Entonces, se observa que W y W estarán expresados en libras. Si se
usan las unidades del SI, se debe expresar a µ en N/m3, a t en metros y a las áreas
A y A en metros cuadrados; entonces, los pesos W y W estarán expresados en
newtons.†
Si se sustituye a W y a W en las ecuaciones de momento (5.1) y
se divide a todos los términos entre t, se obtiene
Si se incrementa el número de elementos en los cuales se divide el área
A y simultáneamente se disminuye el tamaño de cada elemento, se obtiene
en el límite
Estas ecuaciones definen las coordenadas x y y del centro de gravedad
de una placa homogénea. El punto cuyas coordenadas son x_ y y_ también
se conoce como el centroide C del área A de la placa (figura 5.3).
Si la placa no es homogénea, estas ecuaciones no se pueden utilizar para
determinar el centro de gravedad de la placa; sin embargo, éstas aún
definen al centroide del área.
En el caso de un alambre homogéneo de sección transversal uniforme,
la magnitud W del peso de un elemento de alambre puede
expresarse como
†Se
debe señalar que en el Sistema Internacional de unidades generalmente se caracteriza
a un material dado por su densidad _ (masa por unidad de volumen) en lugar de caracterizarlo
por su peso específico _. Entones, el peso específico del material se puede
obtener a partir de la relación
El centro de gravedad de un alambre coincide con el centroide C de
la línea L que define la forma del alambre (figura 5.4). Las coordenadas
x y y del centroide de la línea L se obtienen a partir de las ecuaciones
5.4. PRIMEROS MOMENTOS DE ÁREAS Y LÍNEAS
La integral _ x dA en las ecuaciones (5.3) de la sección anterior se conoce
como el primer momento del área A con respecto al eje y y se representa
con Qy. En forma similar, la integral _ y dA define el primer
momento de A con respecto al eje x y se representa con Qx. Así se escribe
Si comparamos las ecuaciones (5.3) con las ecuaciones (5.5), se observa
que los primeros momentos del área A pueden ser expresados como
los productos del área con las coordenadas de su centroide:
A partir de las ecuaciones (5.6) se concluye que las coordenadas del
centroide de un área pueden obtenerse al dividir los primeros momentos
de dicha área entre el área misma. Los primeros momentos de un
área también son útiles en la mecánica de materiales para determinar
los esfuerzos de corte en vigas sujetas a cargas transversales. Por último,
a partir de las ecuaciones (5.6) se observa que si el centroide de un área
está localizado sobre un eje coordenado, entonces el primer momento
del área con respecto a ese eje es igual a cero. De manera inversa, si el
primer momento de un área con respecto a un eje coordenado es igual
a cero, entonces el centroide del área está localizado sobre ese eje.
Se pueden utilizar relaciones similares a partir de las ecuaciones
(5.5) y (5.6) para definir los primeros momentos de una línea con respecto
a los ejes coordenados y para expresar dichos momentos como los
productos de la longitud L de la línea y las coordenadas x_ y y_ de su centroide.
Se dice que un área A es simétrica con respecto a un eje BB_ si para
todo punto P del área existe un punto P_ de esa misma área tal que
la línea PP_ sea perpendicular a BB_ y dicha línea está dividida en dos
partes iguales por el eje en cuestión (fıgura 5.5a). Se dice que una línea
L es simétrica con respecto a un eje BB_ si satisface condiciones
similares. Cuando un área A o una línea L posee un eje de simetría
BB_, su primer momento con respecto a BB_ es igual a cero y su centroide
está localizado sobre dicho eje. Por ejemplo, en el caso del área
A de la figura 5.5b, la cual es simétriaca con respecto al eje y, se observa
que para cada elemento de área dA de abscisa x existe un elemento
de área dA_ que tiene la misma superficie y cuya abscisa es _x.
Se concluye que la integral en la primera de las ecuaciones (5.5) es
igual a cero y, por tanto, se tiene que Qy _ 0. También se concluye a
partir de la primera de las relaciones (5.3) que x_ _ 0. Por consiguiente,
si un área A o una línea L poseen un eje de simetría, su centroide
C está localizado sobre dicho eje.
Además, se debe señalar que si un área o una línea posee dos ejes
de simetría, su centroide C debe estar localizado en la intersección de
esos dos ejes (figura 5.6). Esta propiedad permite determinar de inmediato
el centroide de áreas como círculos, elipses, cuadrados, rectángulos,
triángulos equiláteros u otras figuras simétricas, así como el centroide
de líneas que tienen la forma de la circunferencia de un círculo,
el perímetro de un cuadrado, entre otros.
Figura 5.7
Figura 5.5
Se dice que un área A es simétrica con respecto a un centro O si
para cada elemento de área dA de coordenadas x y y existe un elemento
de área dA_ de igual superficie con coordenadas _x y _y (figura
5.7). Entonces, se concluye que ambas integrales en las ecuaciones (5.5)
son iguales a cero y que Qx _ Qy _ 0. También, a partir de las ecuaciones
(5.3), se concluye que x_ _ y_ _ 0, esto es, que el centroide del
área coincide con su centro de simetría O. En forma análoga, si una línea
posee un centro de simetría O, el centroide de la línea coincidirá
con el centro O.
Se debe señalar que una figura con un centro de simetría no necesariamente
posee un eje de simetría (figura 5.7) y que una figura con
dos ejes de simetría no necesariamente tiene un centro de simetría (figura
5.6a). Sin embargo, si una figura posee dos ejes de simetría que
son perpendiculares entre sí, el punto de intersección de dichos ejes
es un centro de simetría (figura 5.6b).
La determinación de los centroides de áreas asimétricas y de líneas
y áreas que poseen un solo eje de simetría se estudiará en las secciones
5.6 y 5.7. En las figuras 5.8A y 5.8B se muestran los centroides
de formas comunes de áreas y de líneas.
4.1.3. Placas y alambres compuestos
o en forma condensada
Estas ecuaciones se pueden resolver para las coordenadas X_ y Y_ del
centro de gravedad de la placa.
Si la placa es homogénea y de espesor uniforme, el centro de gravedad
coincide con el centroide C de su área. La abscisa X_ del centroide
del área puede determinarse observando que el primer momento
Qy del área compuesta con respecto al eje y puede expresarse como el
producto de X_ con el área total y como la suma de los primeros momentos
de las áreas elementales con respecto al eje y (figura 5.10). La
ordenada Y_ del centroide se encuentra de forma similar, considerando
el primer momento Qx del área compuesta. Así, se tiene
Estas ecuaciones proporcionan los primeros momentos del área compuesta
o pueden utilizarse para obtener las coordenadas X_ y Y_ de su
centroide.
Se debe tener cuidado de asignarle el signo apropiado al momento
de cada área. Los primeros momentos de áreas, al igual que los momentos
de las fuerzas, pueden ser positivos o negativos. Por ejemplo,
un área cuyo centroide está localizado a la izquierda del eje y tendrá
un primer momento negativo con respecto a dicho eje. Además al área
de un agujero se le debe asignar un signo negativo (fıgura 5.11).
De manera similar, en muchos casos es posible determinar el centro
de gravedad de un alambre compuesto o el centroide de una línea
compuesta dividiendo al alambre o a la línea en elementos más simples
(véase problema resuelto 5.2).
4.1.4. Determinación de centros de gravedad por integración
4.2. Momento de primer orden por integración
4.3. Momento de segundo orden por áreas simples
Para el perfil que se muestra en la figura, cuyas dimensiones son
a = 100 mm,
y
b = 180 mm y
R = 240 mm,
a) Calcular los momentos de segundo orden
Ix, Iy e Ixy.
b) Calcular los momentos principales de inercia
en el punto O.
a
O b
R
x
c) Calcular el ángulo que forman los ejes
principales de inercia OUV con los ejes OXY.
Dibujar los ejes principales de inercia.
a) Para calcular los momentos de segundo orden de la superficie completa
consideramos las mismas figuras que en el ejemplo anterior y buscamos sus
4
momentos en las tablas. Dado que las cantidades en mm serían muy grandes,
pasaremos las unidades a cm.
Los momentos de segundo orden del triángulo son:
y
3
3
3
3
Ix1 = aR /12 = (10 cm) x (24 cm)
Iy1 = Ra /12 = (24 cm) x (10 cm)
R
2 2
a
y
O
x
2
/ 12 = 11520 cm
/ 12 = 2000 cm
4
4
2
Ixy1 = − a R /24 = − (10 cm) x (24 cm) / 24 = − 2400 cm
Los momentos de segundo orden del rectángulo son:
4
3
3
3
3
Ix2 = bR /3 = (18 cm) x (24 cm)
R
Iy2 = Rb /3 = (24 cm) x (18 cm)
2 2
2
Ixy2 = b R /4 = (18 cm)
O
/ 3 = 46656 cm
2
x (24 cm)
4
4
/ 4 = 46656 cm
4
x
b
y
/ 3 = 82944 cm
Los momentos de segundo orden del sector
circular son:
yc
4
4
4
Ix3 = πR /16 = π x (24 cm)
xc
O
R
4
/ 16 = 65144.07 cm
Para calcular el momento de segundo orden con
respecto al eje y, tenemos que buscar en las
tablas el correspondiente a un eje que pase por el
centro de masas y después hay que aplicar el
teorema de Steiner.
x
4
4
4
Iyc3 = (πR /16) − (4R /9π) = (π x (24 cm) /16) − (4 x (24 cm) / 9π) = 18207.37 cm
Para aplicar el teorema de Steiner usamos los datos del ejemplo anterior,
xCM3 = 281.86 mm = 28.186 cm
yCM3 = 101.86 mm = 10.186 cm
A3 = 45238.93 mm
2
= 452.389 cm
2
2
Iy3 = Iyc3 + (xCM3) A3 =
4
2
2
4
= 18207.37 cm + (28.186 cm) x (452.389 cm ) = 377608.08 cm
Para calcular el momento mixto de segundo orden, tenemos que proceder de la
misma forma.
4
4
Ixyc3 = (9π−32)R /72π = (9π−32) x (24 cm) / 72π = − 5464.70 cm
4
Ixy3 = Ixyc3 + xCM3 yCM3 A3 =
4
2
4
= − 5464.70 cm + (10.186 cm) x (28.186 cm) x (452.389 cm ) = 124417.36 cm
Los momentos de segundo orden de la superficie completa serán la suma de los
correspondientes a cada parte,
4
4
4
4
4
4
Ix = Ix1 + Ix2 + Ix3 = (11520 cm ) + (82944 cm ) + (65144.07 cm ) = 159608.07 cm
4
4
Iy = Iy1 + Iy2 + Iy3 = (2000 cm ) + (46656 cm ) + (377608.08 cm ) = 426264.08 cm
Ixy = Ixy1 + Ixy2 + Ixy3 =
4
4
4
4
= (− 2400 cm ) + (46656 cm ) + (124417.36 cm ) = 168673.36 cm
b) Para calcular los momentos principales de inercia utilizamos las expresiones
correspondientes:
4
4
4
4
IR = (Ix − Iy)/2 = (159608.07 cm − 426264.08 cm ) / 2 = − 133328.01 cm
IS = (Ix + Iy)/2 = (159608.07 cm + 426264.08 cm ) / 2 = 292936.08 cm
2
Imax = IS + [(IR)
2 1/2
+ (Ixy) ]
=
4
4
4
4
42
4 2 1/2
42
4 2 1/2
= 292936.08 cm + [(−133328.01 cm ) + (168673.36 cm ) ]
4
2
2 1/2
cm Imin = IS − [(IR) + (Ixy) ]
= 507940.87
=
4
= 292936.08 cm − [(−133328.01 cm ) + (168673.36 cm ) ] = 77931.29
4
cm c) Y el ángulo que forman los ejes principales con los ejes dados, es
-1
-1
2θ p = tg (−Ixy / I R) = tg (−168673.36 / −133328.01) =
51.675º θp = (51.675º) / 2 = 25.838º
y
v
u
a
O b
R
x
Para comprobar si el eje u que forma un ángulo
de 25.838º con el eje x corresponde al eje
principal de momento máximo o mínimo,
podemos usar otra de las expresiones:
Ix' = IS + IR cos 2θp − Ixy sen 2θp =
= 292936.08 + (− 133328.01) cos(51.675º) − (168673.36) sen (51.675º) =
4
= 77931.29 cm
Que corresponde al valor de Imin.
Podríamos haber calculado los momentos principales mediante esta expresión en
lugar de las otras. Para encontrar el otro momento principal bastaría sustituir en la
última expresión el ángulo correspondiente al otro eje: θp + 90º = 115.838º.
Para el perfil que se muestra en la figura, sabiendo que R mide 0.5 m, calcular los
momentos de segundo orden, Iu, Iv e Iuv, respecto a los
y
ejes Auv.
A
R
u
Para calcular los momentos de segundo orden de la
superficie, consideramos las dos figuras que se
O
x
encuentran en las tablas: un cuadrado y un cuarto de
v
círculo.
Podemos calcular los momentos de segundo orden de
cada una de estas figuras con respecto a los ejes Auv (mediante el teorema de
Steiner) y restarlos después para obtener los momentos de la superficie del
problema.
De una forma más sencilla, podemos calcular los momentos de la superficie con
respecto a los ejes Oxy y aplicar después el teorema de Steiner para encontrar los
momentos con respecto a los ejes Auv.
Los momentos de segundo orden del cuadrado, con respecto a los ejes Oxy son:
3
y
4
Ix1 = RR /3 = (0.5 m)
3
4
/ 3 = 0.02083 m
4
Iy1 = R R/3 = (0.5 m)
2 2
4
Ixy1 = R R /4 = (0.5 m)
x
O
/ 3 = 0.02083 m
4
/ 4 = 0.01563 m
4
Los momentos de segundo orden del sector circular son:
y
4
4
4
4
Ix2 = πR /16 = π x (0.5 m)
Iy2 = πR /16 = π x (0.5 m)
O
4
x
/ 16 = 0.01227 m
/ 16 = 0.01227 m
4
4
4
4
Ixy2 = R /8 = (0.5 m) / 8 = 0.00781 m
Dada la simetría de las figuras, encontramos
Ix1 = Iy1 y también Ix2 = Iy2 , por lo que Ix = Iy, como era de esperar.
Los momentos de segundo orden de la superficie completa respecto a los ejes Oxy,
serán la diferencia entre los correspondientes a cada parte,
4
4
Ix = Iy = Ix1 − Ix2 = (0.02083 m ) − (0.01227 m ) = 0.00856 m
4
4
Ixy = Ixy1 − Ixy2 = (0.01563 m ) − (0.00781 m ) = 0.00782 m
4
4
Ahora tenemos que aplicar el teorema de Steiner para encontrar los momentos con
respecto a los ejes Auv. Para ello necesitamos las coordenadas del centro de masas
de la superficie problema con respecto a los
y
yc
nuevos
ejes
Auv.
Podemos
obtener
fácilmente
este
dato
a
partir
de
sus
A
u
coordenadas con respecto a los ejes Oxy
xc
calculadas en un problema anterior (problema
1.3).
x
O
En el sistema Oxy, xG = yG = 0.387 m.
Las coordenadas de este punto en el sistema
Auv serán:
xG
uG= − (R − xG) = − (0.5 − 0.387) = − 0.113 m
v
vG= R − xG = 0.5 − 0.387 = 0.113 m
La coordenada vG es positiva porque la flecha del eje indica que se toma hacia abajo
el sentido positivo en este sistema de referencia.
También necesitaremos el area de la superficie, calculada en el problema 1.3.
2
A = 0.054 m .
Finalmente, aplicamos el teorema de Steiner. Primero una vez para ir a un sistema
que pase por el centro de masas y después otra para ir al sistema Auv.
2
Ix = Ixc + (yG) A →
2
2
-4
Ixc = Ix − (yG) A = 0.00856 − (0.387 x 0.054) = 4.725 x 10
m4
2
2
→
Ixy = Ixyc + xGyGA
2
-4
Iyc = Iy − (xG) A = 0.00856 − (0.387 x 0.054) = 4.725 x 10
Iy = Iyc + (xG) A →
m4
Ixyc = Ixy − xGyGA =
= 0.00782 − (0.387 x 0.387 x 0.054) = − 2.675 x 10
-4
m
4
Ya podemos pasar al sistema Auv. Debemos tener en cuenta que hay que cambiar
el signo de Ixyc porque el eje v tiene definido el sentido positivo de forma opuesta al
eje yc.
2
-4
2
-4
Iu = Ixc + (vG) A = 4.725 x 10
2
4
2
4
+ (0.113 x 0.054) = 0.00116 m
Iv = Iyc + (uG) A = 4.725 x 10
+ (0.113 x 0.054) = 0.00116 m
-4
-4
Iuv = Ixyc + uGvGA = − (− 2.675 x 10 ) + (0.113 x (−0.113) x 0.054) = − 4.22 x 10
4
m
Obviamente, dada la simetría de la superficie, volvemos a encontrar Iu = Iv.
Para el perfil que se muestra en la figura, donde la longitud L mide 1.5 m,
a) Calcular los momentos de segundo orden Ix, Iy e
y
Ixy.
b) Calcular los momentos principales de inercia en el
punto O.
L
c) Dibujar el círculo de Mohr correspondiente.
L
O
L
x
L
a) Para calcular los momentos de segundo orden de la superficie completa
consideramos tres figuras: un rectángulo, un cuarto de círculo y un triángulo, y
buscamos sus momentos en las tablas.
Los momentos de segundo orden del rectángulo son:
3
4
3
4
Ix1 = 2L(L) /3 = 2 x (1.5 m)
/ 3 = 3.375 m
Iy1 = L(2L) /3 = 8 x (1.5 m) / 3 = 13.5 m
2
2
4
4
4
4
Ixy1 = (2L) (L) /4 = 4 x (1.5 m) / 4 = 5.063 m
Los momentos de segundo orden del sector circular son:
4
4
Ix2 = π(L) /16 = π x (1.5 m) / 16 = 0.994 m
4
4
Iy2 = π(L) /16 = π x (1.5 m)
4
4
Ixy2 = (L) /8 = (1.5 m)
4
4
/ 16 = 0.994 m
/ 8 = 0.633 m
4
Los momentos de segundo orden del triángulo son:
Para calcular el momento de segundo orden con
respecto al eje x, tenemos que buscar en las tablas el
correspondiente a un eje que pase por el centro de
masas, xc.
3
4
4
Ixc3 = 2L(L) /36 = 2 x (1.5 m) / 36 = 0.281 m
Para aplicar el teorema de Steiner necesitamos las
coordenadas del centro de masas y el area del triángulo
2
4
2
Ix3 = Ixc3 + (yG3) A3 = (0.281 m ) + (2 m)
2
x (2.25 m ) = 9.281 m
4
Para calcular el momento de segundo orden con respecto al eje y, no es necesario
aplicar Steiner, sino la expresión de las tablas, directamente.
3
4
Iy3 = L(2L) /12 = 8 x (1.5 m)
/ 12 = 3.375 m
4
Para calcular el momento mixto de segundo orden, volvemos a proceder de la
misma forma.
2
2
Ixyc3 = − (2L) (L) /72 = − 4 x (1.5 m)
4
/ 72 = − 0.281 m
4
4
2
Ixy3 = Ixyc3 + xG3 yG3 A3 = (− 0.281 m ) + (1 m) x (2 m) x (2.25 m ) = 4.219 m
4
Los momentos de segundo orden de la superficie completa se obtienen sumando los
correspondientes al rectángulo y el triángulo y restando los del cuarto de círculo,
4
4
4
4
Ix = Ix1 − Ix2 + Ix3 = (3.375 m ) − (0.994 m ) + (9.281 m ) = 11.662 m Iy
4
4
4
4
= Iy1 − Iy2 + Iy3 = (13.5 m ) − (0.994 m ) + (3.375 m ) = 15.881 m Ixy =
4
4
4
Ixy1 − Ixy2 + Ixy3 = (5.063 m ) − (0.633 m ) + (4.219 m ) = 8.649 m
4
b) Para calcular los momentos principales de inercia utilizamos las expresiones
correspondientes:
IR = (Ix − Iy)/2 = (11.662 m
IS = (Ix + Iy)/2 = (11.662 m
2
2 1/2
Imax = IS + [(IR) + (Ixy) ]
4
2
4
4
4
+ 15.881 m ) / 2 = 13.772 m
2
4
4
2 1/2
= (13.772) + [(− 2.110) + (8.649) ]
2 1/2
m Imin = IS − [(IR) + (Ixy) ]
4
− 15.881 m ) / 2 = − 2.110 m
2
= 22.675
2 1/2
= (13.772) − [(− 2.110) + (8.649) ]
= 4.869
4
m Y el ángulo que forman los ejes principales con los ejes dados, es
-1
-1
θp = (1/2) tg (−Ixy / IR) = (1/2) tg (−8.649 / − 2.110) = 38.14º
c) Para dibujar el círculo de Mohr, sólo necesitamos los valores de Ix, Iy e Ixy.
Seguiremos los siguientes pasos:
Trazamos un sistema de ejes y ponemos las escalas correspondientes a los
momentos Ix, I y en el eje de abscisas e Ixy en el eje de ordenadas.
4
Ixy (m )
10
0
0
10
20
4
Ix, Iy (m )
-10
Representamos los puntos A (Ix, Ixy) y B (Iy, − Ixy), que en este caso corresponden a
A (11.662, 8.649) y B (15.881, − 8.649). A continuación unimos estos dos puntos
mediante una linea recta. El punto de esta linea que corta el eje de abscisas será el
centro del círculo de Mohr (C).
4
Ixy (m )
10
A
0
0
10
20
C
4
Ix, Iy (m )
B
-10
Trazamos un círculo con centro en el punto C y con la distancia AC como radio.
4
Ixy (m )
10
A
0
0
-10
10
C
20
4
Ix, Iy (m )
B
Este círculo corta el eje de abscisas en dos puntos. El más próximo al origen
corresponde al momento mínimo, Imin, y el más lejano al momento máximo, Imax.
Para conocer sus valores, gráficamente, bastará con leer su valor en las escalas
graduadas de los ejes.
4
Ixy (m )
10
0
0 Imin
10
20
4
Ix, Iy (m )
Imax
-10
4
4
Para este caso, podemos ver que Imin ≅ 5 m e Imax ≅ 22.8 m , en buen acuerdo
4
con los valores obtenidos matemáticamente Imin = 4.869 m e Imax = 22.675 m
4