Capa Límite Esquema de cálculo Capa Límite en una placa plana

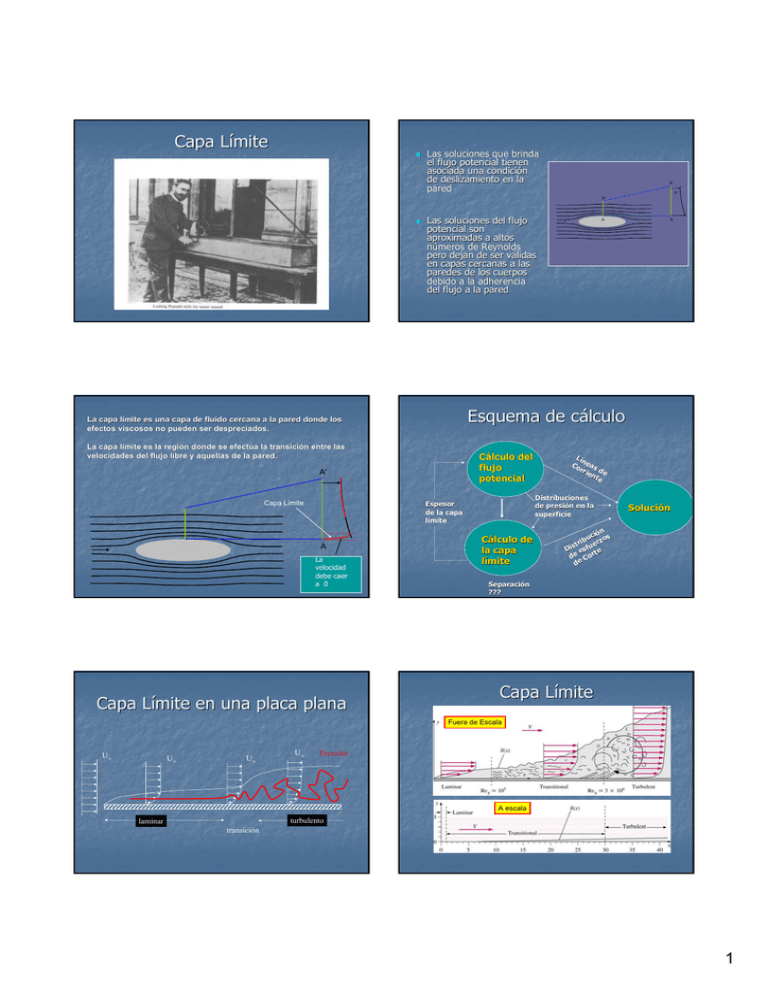
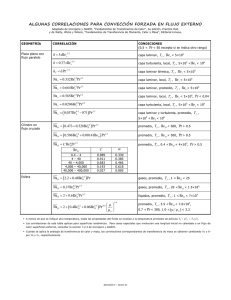
Capa Límite
„
Las soluciones que brinda
el flujo potencial tienen
asociada una condición
de deslizamiento en la
pared
A'
U
A'
„
Las soluciones del flujo
potencial son
aproximadas a altos
números de Reynolds
pero dejan de ser válidas
en capas cercanas a las
paredes de los cuerpos
debido a la adherencia
del flujo a la pared
La capa límite es la regió
región donde se efectú
efectúa la transició
transición entre las
velocidades del flujo libre y aquellas de la pared.
Cálculo del
flujo
potencial
A'
La
velocity
drops
velocidad
to 0
debe caer
a 0
Capa Límite en una placa plana
Lí n
Co eas
rri
d
en e
te
Distribuciones
de presión en la
superficie
Espesor
de la capa
límite
A
A
Esquema de cálculo
La capa límite es una capa de fluido cercana a la pared donde los
efectos viscosos no pueden ser despreciados.
despreciados.
Capa Límite
A
Cálculo de
la capa
límite
Solución
n
ció s
ibu erzo
str
Di esfu te
d e Co r
de
Separación
???
Capa Límite
Fuera de Escala
U∞
U∞
U∞
U∞
Trazador
A escala
turbulento
laminar
transición
1
Transición en la capa límite
Capas límites
• La transición de regimen laminar a regimen
turbulento en el flujo dentro de la capa límite depende
del número de Reynolds definido como
Re x =
turbulent
laminar
ρU x
µ
leading edge
ρ = densidad del fluido,
U = velocidad de la corriente libre,
x = distancia al borde de ataque,
µ = viscosidad dinámica.
•Zona de Transición comienza Rex~ 105
Video
x
donde:
Laminar
• Movimiento
Uniforme y
Regular.
•La capa límite comienza a ser turbulenta para Rex~ 3 105
Perfiles de Velocidad en la capa
límite
Turbulento
•Movimiento irregular y no
estacionario
• Mezclado importante entre las
distintas capas.
La capa límite turbulenta llega a la superficie!
x
δlam ≈10−2 −10−1 mm
δturb ≈10− 30 mm
Resistencia al avance del cuerpo
Video
4
Estructura de la Capa límite
Turbulenta
3
1
Capa Interna ~2~2-6mm
Flujo
Espesor
Tensiones de
Re vs
Tensiones
viscosas
2-Región
Logarítmica
3-Region externa
Intermitente
trubulento
Turbulento
c/fuertes fluc.
fluc.
veloc
Turbulento c/fluct
c/fluct Con algunas
moderadas
característ.
característ.
perturb por la
laminares
intermit.
intermit.
40 υ
u*
Tensiones viscosas
predominantes
„
Arrastre de Superficie:
Superficie:
„
Capa externa ~8~8-25mm
1-Subcapa viscosa
0< y<
2
0.2δ < y < δ
40 υ
< y < 0.2δ
u*
Tensiones
Reynolds
predominantes
Tensiones
Reynolds
predominantes
„
4-Supercapa
viscosa
„
Arrastre de forma
u * = veloc . frotam =
pared
ρ
=
σ xy '
=
ρ
(u ' v ')
Video
U
Video
y > 0.4δ
Tensiones
Reynolds
predominantes
„
„
σ xy
U
Fuerzas de fricción causadas por el
cisallamiento entre la superificie y el fluido
Area superf. y ______del
largo
Son función de ___________
objeto
„
Fuerzas causadas por las diferencias de presión
en el cuerpo.
cuerpo.
Dependen del contorneo y pegado de la capa
límite al cuerpo
Area Normal al flujo
Son function del ___________________
2
Flujo de Couette Poisseuille
Separación de la capa límite
y
.
Se admite
U
r
u = ( f ( y ), 0, 0)
x
P2
P1
∂p
= cte = −k
∂x
wake
u( y) =
Gradientes de Presión
„
−k 2 y y
y
h 1−
+U
2 µ  h  h
h
Gradientes de presión
La forma de la capa límite es fuertemente
influenciada por los gradientes de presión
externos
(a) favorable (dP/dx < 0)
(b) cero
(c) Moderadamente adversos (dP/dx >
0)
(d) Gradiente crítico adverso (τw = 0)
(e) Fuertemente adverso (flujo
separado)
separado)
Separación de la capa límite
laminar o turbulenta
„
„
CD =
La aproximación de la
capa límite deja de ser
válida luego del punto de
separación debido al flujo
inverso.
inverso.
La capa límite turbulenta
es más resistente a los
gradientes adversos de
presión
Laminar flow separates at corner
Turbulent flow does not separate
2F
ρ U ∞2 b D
Video
Laminar
video
Turbulent
Video
Video 15º
Video
Video 20º
Video
3
Cd =
„
2 Drag
ρU 2 A
Drag =
C d ρU 2 A
2
Ford Explorer 2002 Cd = 0.41
Video
Coordenadas de la Capa Límite
Llamamos x a la coordenada de la capa límite en la direcció
dirección del
flujo,
flujo, e y a la coordenada de la capa límite en la direcció
dirección normal.
Si el espesor de la capa límite δ(x)
δ(x) es muy delgado frente al radio
de curvatura R de la pared
δ(x) <<R
Video
N S en coordenadas capa límite
~
N S en coordenadas cartesianas
La capa límite se desarrolla como si la pared fuese plana
y
δ(x)
x
Ordenes de Magnitud de la capa límite
2D NAVIERNAVIER-STOKES y Ecuació
Ecuación de Cons. De la Masa
Vamos analizar los ordenes de magnitud de los distintos términos de
las ecuaciones con los siguientes considerandos
Llamando L a la escala longitudinal y δ a la escala transversal
 ∂ 2u ∂ 2u 
1 ∂p
∂u
∂u
u
+v
=−
+ ν  2 + 2 
ρ ∂x  ∂x ∂y 
∂y
∂x
 ∂ 2v ∂ 2v 
∂v
∂v
1 ∂p
+ ν  2 + 2 
u +v = −
∂x
∂y
ρ ∂y  ∂x ∂y 
δ << L
∂( ) ( )
≈
∂x
L
∂( ) ( )
≈
δ
∂y
∂u ∂v
+
=0
∂x ∂y
En cuanto a la velocidad siendo U la velocidad del flujo libre
∂u
U
≈
∂( ) ( )
Ecuación de continuidad
v~
τ conv
δ2
υ ⇒δ =
x
=
U
x
υ
U x
=
1
Re x
δ
L
δ
U
v~
L
δ
L
U≈
υ
UL
<< 1 ⇒ v → 0
Como V ~ (δ
(δ/L)U y
multiplicando todos los
términos por (δ/U2), se
obtiene
Como (δ
(δ/L) ~ (Re)-1/2
U=
 ∂ 2v ∂ 2v 
1 ∂p
∂v
∂v
+v = −
+ ν  2 + 2 
ρ ∂y
∂x
∂y
∂y 
 ∂x
UV
V2
,
L
δ
∂u U
~
∂x L
τ dif =
u
∂v
∂u
=−
∂y
∂x
∂u ∂v
+
=0
∂x ∂y
Video
Ec. de cons de la cant de movim. en la dir. normal
υU
L
Re>>1
2
δ 
δ 
  ,  
 L
 L
1
Re
,
1
Re
,
U2
δ
, ν
2
V
V
, ν 2
L2
δ
2
, 1 ,
1 δ 
1
  ,
Re  L  Re
, 1 ,
∂p
∂y
1
Re 2
,
1
Re
=0
4
APROXIMACION DE NS DE LA CAPA LIMITE
∂p
∂y
Las ecuaciones de la capa límite son entonces:
=0
∂u
∂u
1 dp pdb
∂ 2u
+v
=−
+ν 2
∂x
∂y
ρ dx
∂y
∂u ∂v
+
=0
∂x ∂y
u
Inidica que la presión es constante según la coordenada “y” dentro de
la capa límite
Sea ppd(x,y) la presión
obtenida a partir de la solución
U
de flujo potencial. Surge
entonces que pd(x) puede ser
obtenida a partir de ppd(x,0):
y
δ(x)
x
L
donde ppdp(x) es conocida y
surge de considerar el
escurrimiento potencial
u y =0 = 0 ,
Solución de Blasius
„
„
Blasius considera el caso
de una placa plana y el
flujo externo a considerar
es en ese caso
La solución a la que llega
es una solución numérica
sin expresión analítica en
función de una variable
adimensional
U = cte ⇒
∂p
=0
∂x
δ( x )
U
y
0
1/ 2
 U



es máximo
du
en el borde
dy
de atatque
L
U
v y =0 = 0
Adicionalmente u debe aproximarse al valor
de la velocidad del flujo potencial U si y
crece y se acerca a la capa límite.
• La capa límite crece con: δ ∝
√x
• El crecimiento inicial es
rápido
• El crecimiento de la capa
límite dδ/dx ∝ 1/√
1/√x, decrece
hacia aguas abajo
0
0.5
x
1
10
τ w( x )
U
δ
x
δ(x)
x
U
0.5
η = y ∞ 
2υ x
5
Espesor
de la capa
límite
Esfuerzo
de corte
en la
pared
0
0.5
x
1
• Las tensiones en la pared: τw
∝ 1/√
1/√x
• A medida que aumenta el
espesor de la capa límite,
mite, la
tensió
tensión de corte disminuye
porque disminuye el gradiente
de velocidades.
velocidades.
Flujos y Cantidad de Movimiento para un volumen
de control rectangular
Capa límite en una placa plana
U
dU
dx
y
1
0
τo
=U
Las condiciones de borde son
El flujo externo a la capa límite deja su
impronta en la capa límite a través de la
presión.
pd ( x ) = ppd ( x,0) ≡ ppdb ( x )
1 dp pdb
ρ dx
(1)
h
(2)
(3)
τ0
Sección
Flujos
∑
(1)
flujos = 0
b
Cant Mov s/x
∑
Flujos c.de mov = Arrastre
h
h
∫
U dy
∫
ρb U 2 dy
0
0
(2)
δ
(4)
h
h
∫
− b u dy
∫
− ρb u 2 dy
0
0
(3)
h
−b
∫(
U − u ) dy
0
(4)
0
h
∫
− ρb U (U − u ) dy
0
0
5
Espesor de Desplazamiento
Flujo Inviscido
Espesor de Cantidad de Movimiento
Flujo Viscoso
Flujo Inviscido
Flujo Viscoso
∞
∫
∞
δ1 b U =
∫
(U − u ) b dy
0
0
δ1
∞
⇒ δ1 =
∫
ρ δ 2 b U 2 = ρ u (U − u ) b dy
(1 −
δ2
u
)dy
U
(3)
∂δ ( x )
dx
∂x
∫
„
(2)
„
u 2 dy
„
0
F1x = pδ (x )
∂F1x
∂x
∂δ ( x )
dx
F3 x = p
∂x
F4 x = −τ 0 dx
∫
M F 2x
F2 x = F1x +
M F 3x
∂M F 1x
dx
= M F 1x +
∂x
 δ ( x)



∂ ρu 2 dy 


0
 dxU
= dm& U = 
∂x
∫
Métodos Integrales para capa límite
laminar en placa plana
„
Hay que suponer una función u(x,y)
u(x,y) que cumpla
Una opción es
π y 
u = U sen

2δ
τ0 = µ
du
dy
Y la expresión de
∞
u
espesor de cant.
cant. de
δ 1 = (1 − )dy
desplazamiento y de
U
0
cantidad de
∞
movimiento
u
u
δ2 =
(1 − )dy
Se obtiene la
U
U
0
siguiente ecuación
diferencial
dδ 2 1 dU
(2δ 2 + δ1 ) = τ 0 2
+
dx U dx
ρU
∫
„
∂ (u ( x, y ) )
=0
∂y
y =δ
Hay que suponer una función u(x,y)
u(x,y) que cumpla
„
Una opción es
δ (0) ⇒ C = 0
πU
µ
δ2
4 − π dδ
2π π xυ
xυ
= 2 δ2 ⇒
=
+
C
δ = 4.79
U
ρU
2π dx
2 4 −π 2 U 2
1
∂ (u ( x, y ) )
=0
∂y
y =δ
7
τ0
 υ 
= 0.0225

ρU 2
 Uδ 
πU
2δ
1
4
δ
Turbulento
τ
7 dδ
= 0
72 dx ρU 2
δ Blasisus
xυ
=5
U
u ( x,0) = 0
u ( x, δ ) = U
u  y
= 
U δ 
=µ
y =0
Fix
i
u ( x, δ ) = U
π −2
δ1 =
δ
π
4 −π
δ2 =
δ
2π
∑
Métodos Integrales para capa límite
Turbulenta en placa plana
u ( x,0) = 0
„
M Fix =
∫
δ ( x)
M F 1x = ρ
∑
Considerando que
i
δ(x)
x+dx
u
u
(1 − )dy
U
U
0
 δ ( x)



∂ ρ u dx 


dm&
0

 dx
dm& = m& x + dx − m& x =
dx =
dx
∂x
(4)
∫
Flujos c. de
mov. iguales
Métodos Integrales de la capa límite
x
⇒ δ2 =
0
Areas
iguales
(1)
∞
 Uυ 
= 0.37 

x − x0
 x − x0 
δ
Lam.
−1 / 5
x0
Re
6
Capa límite turbulenta
Turbulent Boundary Layer
„
Ley de la pared en capas límites
Black lines: instantaneous
Pink line: time-averaged
u* =
Perfil de velocidades en coordenadas
de la pared
τp
ρ
u
u*
u* =
Comparación de los
perfiles laminares y
turbulentos de la cl
y*=yu*/η
Coeficientes de fricción en una placa plana
Capa Límite turbulenta
Cd =
f
Spalding (1961) desarrollo una fórmula
que es válida en gran parte de la capa
límite
Cd f =
Cd f
1.328
( Rel )
0.5
e
l
Cd f = 0.072 Rel−0.2
Rel =
Resúmen capa limite turbulenta
−2.5
1 x 10-3
5 x 10-4
2 x 10-4
1 x 10-4
5 x 10-5
2 x 10-5
-5
1 x 10-6
5 x 10-6
2 x 10-6
1 x 10
0.001
κ, B son constantes
10
00
0
„
Cd f = 1.89 − 1.62log ( ε / l ) 
0.01
10
00
00
0
10
00
00
00
10
00
00
00
0
10
00
00
00
00
10
00
00
00
00
0
„
τ0
ρU 2
10
00
00
Ilustración de las fluctuaciones
en la capa límite turbulenta
Ul
ν
Conclusiones
„
„
„
„
„
„
En esta clase vimos cuales son las hipotesis que se
adoptan para simplificar las ecuaciones de conservación
en el caso de querer analizar el movimiento del fluido
dentro de la capa límite
Existen dos parámetros que resultan de particular interés:
el espesor de la capa límite y el coeficiente de fricción
Los valores de dichos parámetros difieren fuertemente
según si el flujo es laminar o turbulento en el interior de la
capa límite
A señalar es que en tanto que en la región laminar δ~x1/2
en la región turbulenta δ~x
Los coeficientes de fricción local son un orden de
magnitud superiores en el caso de flujos turbulentos
Una medida de estos efectos la dan los espesores de
desplazamiento y de cantidad de movimiento.
movimiento.
7