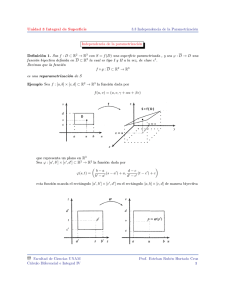
Ejercicios resueltos. 1. Sea la curva intersección de la superficie G φ

E.T.S.
Arquitectura
Curvas y super…cies.
Ejercicios resueltos.
1. Sea la curva intersección de la super…cie z = xy con el cilindro parabólico
y = x2 . Se pide:
(a) En el punto P de coordenadas (0; 0; 0), obtener la ecuación del
plano osculador de la super…cie en P y la recta normal a la super…cie
en P .
Solución.
Una parametrización de dicha curva es la siguiente:
(t) = t; t2 ; t3 ;
t 2 R:
Se tiene:
0
1; 2t; 3t2 ; t 2 R;
p
0
1 + 4t2 + 9t4 6= 1
k (t)k =
(t) =
luego no es la parametrización natural.
(b) En el punto P de coordenadas (0; 0; 0), obtener las proyecciones de
la curva sobre los planos del Triedro de Frenet.
Solución.
Hallamos los planos del triedro de Frenet en P . Primero calculamos
el vector tangente, el normal y el binormal en P . Tenemos:
t; t2 ; t3 = (0; 0; 0) =) t = 0, luego P = (0);
00
(t) = (0; 2; 6t) ;
~t(t) =
0
(t) ^
00
p
1; 2t; 3t2 luego ~t(0) = (1; 0; 0)
i j k
1 2t 3t2 = 6t2 ; 6t; 2 ;
0 2 6t
(t) =
~b(t) =
1
1+4t2 +9t4
p
1
4+36t2 +36t4
6t2 ; 6t; 2 luego ~b(0) =
p1
4
(0; 0; 2) = (0; 0; 1);
i j k
~
~n(0) = b(0) ^ ~t(0) = 0 0 1 = (0; 1; 0) :
1 0 0
Por tanto, las ecuaciones de los planos del Triedro de Frenet en el
punto P son:
E.T.S. Arquitectura.
Curvas y Super…cies
!
Plano osculador: P X ~b(0) = 0 () (x; y; z) (0; 0; 1) = 0 ()
z = 0.
!
Plano normal: P X ~t(0) = 0 () (x; y; z) (1; 0; 0) = 0 () x =
0.
!
Plano recti…cante: P X ~n(0) = 0 () (x; y; z) (0; 1; 0) = 0 ()
y = 0.
Luego las proyecciones de la curva sobre los planos del triedro de
Frenet son:
Proyección sobre el plano osculador: 1 (t) = t; t2 ; 0 , t 2 R.
Nótese que es la parábola y = x2 en el plano z = 0.
Proyección sobre el plano normal: 2 (t) = 0; t2 ; t3 , t 2 R.
Proyección sobre el plano recti…cante: 3 (t) = t; 0; t3 , t 2 R.
(c) En el punto P de coordenadas (0; 0; 0), obtener la curvatura y la
torsión de la curva.
Solución. La torsión en P es:
[ 0 (0); 00 (0); 00 (0)]
(0) =
:
k 0 (0) ^ 00 (0)k2
Teniendo en cuenta
8
0
(t) = 1; 2t; 3t2
>
>
<
00
(t) = (0; 2; 6t)
000
(t) = (0; 0; 6)
>
>
: 0
00
(t) ^ (t) = 6t2 ; 6t; 2
tenemos:
8
>
>
<
0
(0) = (1; 0; 0)
(0) = (0; 2; 0)
=)
000
(0) = (0; 0; 6)
>
>
: 0
(0) ^ 00 (0) = (0; 0; 2)
00
1 0 0
1
12
(0) =
0
2
0
=
= 3:
4
k(0; 0; 2)k2 0 0 6
La curvatura en P es:
k 0 (0) ^ 00 (0)k
:
(0) =
k 0 (0)k3
Teniendo en cuenta
0
0
tenemos:
(0) = (1; 0; 0)
(0) ^ 00 (0) = (0; 0; 2)
k 0 (0) ^ 00 (0)k
(0) =
= 2:
k 0 (0)k3
E.T.S. Arquitectura.
Curvas y Super…cies
2. Sea la curva del parabolide z = x2 + y 2 que se proyecta verticalmente
sobre la parábola y 2 = x, z = 0. Se pide el ángulo que forman las
rectas tangentes en los puntos P1 = (0; 0; 0) y P2 = (1; 1; 2).
Solución. Una parametrización de dicha curva es la siguiente. La
curva es la intersección del parabolide z = x2 + y 2 con el cilindro
parabólico y 2 = x.
Como y 2 = x, tomo x = t y por tanto, z = t2 +(t2 )2 = t2 +t4 . Tenemos:
(t) = t2 ; t; t2 + t4 ;
t 2 R:
Luego,
0
(t) = 2t; 1; 2t + 4t3 ;
y
t 2 R;
t2 ; t; t2 + t4 =) t = 0 luego P1 = (0);
t2 ; t; t2 + t4 =) t = 1 luego P2 = (1):
(0; 0; 0) =
(1; 1; 2) =
Por tanto, de
0
(0)
0
(1) = k 0 (0)k k 0 (1)k cos ;
0
(0) = (0; 1; 0) ;
0
(1) = (2; 1; 6) ;
obtenemos:
cos
=p
1
1
=p :
4 + 1 + 36
41
E.T.S. Arquitectura.
Curvas y Super…cies
3. Sea S la super…cie de revolución obtenida al girar alrededor del eje X
la curva de ecuaciones cartesianas: y = ex , z = 0.
Se pide:
(a) Una representación paramétrica regular de S.
Solución. La matriz de giro alrededor del eje X es:
0
1
1
0
0
@ 0 cos
sin A
0
sin cos
y una parametrización de la curva es: (t) = (t; et ; 0), t 2 R. Por
tanto,
1
0
1
0
0
:
t et 0 @ 0 cos
sin A = t et cos et sin
0
sin cos
Una representación regular de S es:
~r(t; ) = t; et cos ; et sin
;
t 2 R;
2 [0; 2 ).
(b) Puntos singulares de dicha parametrización.
Solución. Tenemos:
~rt (t; ) =
~r (t; ) =
1; et cos ; et sin ;
0; et sin ; et cos :
Luego,
i
~rt (t; )^~r (t; ) = 1
0
j
e cos
et sin
t
k
e sin
et cos
t
= (et ; et cos ; et sin ):
Como et > 0, el vector ~rt (t; ) ^ ~r (t; ) no se anula para ningún
valor de t ni de .
(c) Clasi…car los puntos de la super…cie.
Solución. Tenemos:
~ (t; ) =
N
=
~rtt (t; ) =
~rt (t; ) =
~r (t; ) =
~rt (t; )^~r (t; )
t
p1
k~rt (t; )^~r (t; )k = 2e2t (e ;
p1 (1;
cos ; sin )
2
t
t
0; e cos ; e sin ;
0; et sin ; et cos ;
0; et cos ; et sin :
et cos ; et sin )
E.T.S. Arquitectura.
Curvas y Super…cies
Por tanto, los coe…cientes de la segunda forma fundamental de S
en un punto arbitrario son:
~ (t; ) = p1 et ;
L(t; ) = ~rtt (t; ) N
2
~ (t; ) = 0;
M (t; ) = ~rt (t; ) N
~ (t; ) = p1 et :
N (t; ) = ~r (t; ) N
2
Por tanto, la matriz de la segunda forma fundamental en un punto
arbitrario P de la super…cie es:
!
p1 et
0
2
IIP =
:
p1 et
0
2
Como det IIP < 0 todos los puntos de la super…cie son hiperbólicos.
(d) Direcciones asintóticas en cualquier punto P de la super…cie.
Solución. Las direcciones asintoticas son aquellas direcciones
(h; k) del plano tangente tales que IIP (h; k) = 0, por tanto, cumplen
lo siguiente:
!
p1 et
0
h
2
IIP (h; k) = h k
1
t
p e
k
0
2
=
=
p1 et h2 + p1 et k 2 = p1 et
2
2
2
p1 et (k + h) (k
h) = 0
2
k2
h2
luego son las direcciones (1; 1) y (1; 1).
(e) ¿Son ortogonales las direcciones asintóticas en cualquier punto P
de la super…cie?
Solución. Calculamos la matriz de la primera forma fundamental
en un punto P arbitrario. Tenemos:
~rt (t; ) ~rt (t; ) = 1 + et ;
~rt (t; ) ~r (t; ) = 0;
~r (t; ) ~r (t; ) = et ;
y, por tanto, la matriz de la primera forma fundamental en un
punto arbitrario P de la super…cie es:
IP =
1 + et 0
0
et
:
Por tanto, el ángulo que forman las direcciones asintóticas (1; 1)
y (1; 1) son:
IP ((1; 1); (1; 1))
cos =
IP ((1; 1); (1; 1))1=2 IP ((1; 1); (1; 1))1=2
E.T.S. Arquitectura.
Curvas y Super…cies
Como
IP ((1; 1); (1; 1)) =
1
1
1 + et 0
0
et
1
1
= 1 6= 0
las dos direcciones asintóticas no son ortogonales.
(f) Curvaturas principales y direcciones principales en un punto P arbitrario.
Solución. La matriz de la aplicación de Weingarten es:
!
1
1 t
t
p
e
0
1+e 0
2
A = (IP ) 1 IIP =
1
t
p et
0
0
e
2
!
p1 e2t
0
2
=
:
p1 et (et + 1)
0
2
Por tanto, las curvaturas principales son k1 = p12 e2t y k2 =
p1 et (et + 1). Y las correspondientes direcciones principales son:
2
~v1 = (1; 0) y ~v2 = (0; 1).
E.T.S. Arquitectura.
Curvas y Super…cies
4. Se considera la super…cie reglada engendrada por la rectas paralelas al
plano x z = 5 que se apoyan en las siguientes curvas:
C1 =
C2 =
(x; y; z) : y = x2 ; z = 0 ;
(x; y; z) : y = z 2 ; x = 0 :
Se pide:
(a) Obtener una parametrización de dicha super…cie.
Solución. Parametrizamos primero las curvas dadas. Tenemos:
1 (t)
=
2 (s) =
t; t2 ; 0 ;
s2 ; 0; s :
Las rectas que unen un punto arbitrario de C1 con cualquier otro
de C2 es de la forma:
!
s2 t; t2 ; s :
1 (t) 2 (s) =
Como queremos rectas paralelas al plano x z = 5 que tiene vector
característico (1; 0; 1) (los vectores del plano son ortogonales al
vector (1; 0; 1)) imponemos la siguiente condición:
!
0 = 1 (t) 2 (s) (1; 0; 1)
=
s2 t; t2 ; s (1; 0; 1)
= s2 t s:
Por tanto, t = s2 s y las rectas de la super…cie en cada punto
tienen la dirección del vector:
!
2
w(s)
~
= 1 (s) 2 (s) = s;
s2 + s ; s :
Luego una parametrización de la super…cie es:
~r(s; ) = ~ (s) + w(s)
~
con ~ (s) =
2 (s)
y w(s)
~
=
!
1 (s) 2 (s)
luego
~r(s; ) = ~ (s) + w(s)
~
=
=
s2 + s;
s2 ; 0; s +
s2 + s
2
s;
s2 + s
;s + s ;
s 2 R;
(b) Estudiar si es alabeada o desarrollable.
Solución. Tenemos:
p(s) =
=
~ 0 (s); w(s);
~
w
~ 0 (s)
2s
s
1
0
1
2
s2 + s
s
2
2 s + s (2s + 1) 1
2
;s
2 [0; 1]:
E.T.S. Arquitectura.
Curvas y Super…cies
Restando la tercera columna a la primera y sacando fuera del determinante el factor s2 + s de la segunda columna obtenemos:
2s
s
1
2
0
1
2
s2 + s
s
2 s2 + s (2s + 1) 1
2s 1
0
0
=
s +s
=
=
s2 + s ( 2s
s2 + s ( 2s
0
1
s2 + s s
2 (2s + 1) 1
1)
s2 + s + 2s (2s + 1)
1) s (3s + 1) 6= 0:
Por tanto, como p(s) 6= 0 la super…cie es no desarrollable.
(c) Clasi…car los puntos de la super…cie.
Solución. Sabemos que para los valores de s en los que p(s) = 0
los puntos son parabólicos y en el resto de caso son hiperbólicos.
Por tanto, como
p(s) = s2 (s + 1) ( 2s
1) (3s + 1) = 0
si y sólo si: s = 0, s = 1, s = 1=2 y s = 1=3 entonces
sustituyendo en la expresión de la parametrización tenemos:
~r(0;
~r( 1;
~r( 1=2;
~r( 1=3;
)
)
)
)
=
=
=
=
(0; 0; 0) ; 8 2 [0; 1];
( 1
; 0; 1
) ; 8 2 [0; 1];
( 1=4
=2;
=16; 1=2
=2) ; 8 2 [0; 1];
( 1=9
=3; 4 =81; 1=3
=3) ; 8 2 [0; 1]:
Las curvas anteriores son curvas de puntos parabólicos.
E.T.S. Arquitectura.
Curvas y Super…cies
5. Se considera el punto P de coordenadas
de Enneper con parametrización:
~r(u; v) =
u
u3
+ uv 2 ; v
3
2
3 ; 0; 1
v3
+ u2 v; u2
3
de la super…cie mínima
v2 ;
(u; v) 2 R2 :
Se pide:
(a) Hallar la segunda forma fundamental de la super…cie en el punto
P.
Solución. Se tiene:
8
3
8
2
u3
2
u u3 + uv 2 = 23
>
u 3 + uv = 3
<
<
2
2
3
~r(u; v) =
; 0; 1 ()
v 1 v3 + u2 = 0
v v3 + u2 v = 0 ()
>
:
3
:
u2 v 2 = 1
u2 v 2 = 1
2
Por tanto, ó v = 0 ó 1 v3 +u2 = 0. Si v = 0, de la tercera ecuación
obtenemos que o bien u = 1 o bien u = 1. Sustituyendo v = 0 y
u = 1 en la primera ecuación obtenemos:
1
2 2
1+ =
6=
3
3 3
luego no puede ser que u = 1. Si u = 1 entonces la primera
ecuación se satisface. Luego: ~r(1; 0) = P . Tenemos
~ru (u; v)
~rv (u; v)
~ruu (u; v)
~ruv (u; v)
~rvv (u; v)
= 1 u2 + v 2 ; 2uv; 2u ;
= 2uv; 1 v 2 + u2 ;
2v ;
= ( 2u; 2v; 2) ;
= (2v; 2u; 0) ;
= (2u;
2v;
2) :
Por tanto,
~ru (1; 0) = (0; 0; 2) ;
~rv (1; 0) = (0; 2; 0) ;
~ (1; 0) = ( 1; 0; 0);
N
8
< ~ruu (1; 0) = ( 2; 0; 2) ;
~ruv (1; 0) = (0; 2; 0) ;
:
~rvv (1; 0) = (2; 0;
2) ;
y la matriz de la segunda forma fundamental en P es:
IIP =
=
~ (1; 0) ~ruv (1; 0)
~ruu (1; 0) N
~ (1; 0) ~rvv (1; 0)
~ruv (1; 0) N
2
0
0
2
:
~ (1; 0)
N
~ (1; 0)
N
!
E.T.S. Arquitectura.
Curvas y Super…cies
(b) Hallar las curvaturas principales y las direcciones principales.
Solución. La matriz de la primera forma fundamental es:
IP =
=
~ru (1; 0) ~ru (1; 0) ~ru (1; 0) ~rv (1; 0)
~ru (1; 0) ~rv (1; 0) ~rv (1; 0) ~rv (1; 0)
4 0
0 4
:
Luego la matriz de la aplicación de Weingarten es:
A =
=
=
1
4 0
0 4
1
4
0
1
2
0
2
0
0
2
0
1
4
0
1
2
0
2
0
2
:
Las curvaturas principales son: k1 = 12 que se alcanza en la dirección
(1; 0) y k2 = 21 que se alcanza en la dirección (1; 0).
(c) Hallar las direcciones asintóticas.
Solución. Vamos a calcular en qué dirección la curvatura es cero.
Por el teorema de Euler tenemos que la curvatura en una dirección
que forma un ángulo con la dirección principal ~e1 = 1=2 (1; 0)
es:
k = k1 cos + k2 sin :
Por tanto, si k = 0 tenemos:
0=
1
cos
2
1
sin
2
() cos
= sin
()
=
4
:
Por
)(1; 0) =
4p
p tanto,
p en la dirección del vector ~v = cos( 4 )(0; 1)+sin(
p
( 2=2; 2=2) la curvatura es cero. La dirección (0; 2=2; 2=2) es
una dirección asintótica. Comprobación: las coordenadas
p del vecp
tor ~v en la base (~ru (1; 0); ~rv (1; 0)) son (cos( 4 ); sin( 4 )) = ( 2=2; 2=2)
y tenemos:
p
p
p
2 0
p2=2 = 0:
( 2=2; 2=2)
0 2
2=2
(d) Clasi…car el punto P .
Solución. El punto P es un punto hiperbólico.
E.T.S. Arquitectura.
Curvas y Super…cies
6. Hallar la arista de retroceso de la super…cie desarrollable con parametrización:
~r(s; t) = 3t2 s
2t3
3t2 ; 4ts
2t2
4t
1; s
Solución. Tenemos:
~r(s; t) = 3t2 s 2t3 3t2 ; 4ts 2t2 4t 1; s
=
2t3 3t2 ;
2t2 4t 1; 1 + s 3t2 ; 4t; 1 ;
= ~ (t) + sw(t):
~
Por tanto,
~ (t)
w(t)
~
~ 0 (t)
w
~ 0 (t)
=
2t3 3t2 ;
= 3t2 ; 4t; 1 ;
=
6t2 6t;
= (6t; 4; 0) ;
2t2
4t
i
0
~ (t) ^ w(t)
~
=
6t2 6t
3t2
= ( t
4t
4; 0 ;
j
k
4t 4 0
4t
1
i j k
1) 6t 4 0
3t2 4t 1
= ( t 1) 4;
= 2( t 1) 2;
6t; 24t2 12t2
3t; 6t2 ;
i j k
w
~ (t) ^ w(t)
~
= 6t 4 0 = 4;
3t2 4t 1
0
(w
~ 0 (t) ^ w(t))
~
(~ 0 (t) ^ w(t))
~
2
= 4( t 1) 2;
3t; 6t
2;
2
4
= 4( t 1) 4 + 9t + 36t
2
kw
~ 0 (t) ^ w(t)k
~
1; 1 ;
= 4;
6t; 12t2
4;
= 4(4 + 9t2 + 36t4 ):
6t; 12t2
3t; 6t2
6t; 12t2
Por tanto,
4( t 1) 4 + 9t2 + 36t4
(w
~ 0 (t) ^ w(t))
~
(~ 0 (t) ^ w(t))
~
=
2
4(4 + 9t2 + 36t4 )
kw
~ 0 (t) ^ w(t)k
~
= ( t 1):
E.T.S. Arquitectura.
Curvas y Super…cies
Por tanto, la arista de retroceso es:
~ (t) = ~ (t)
( t
1)w(t)
~
= ~ (t) + (t + 1)w(t):
~