CUADRILÁTEROS EN EL PLANO

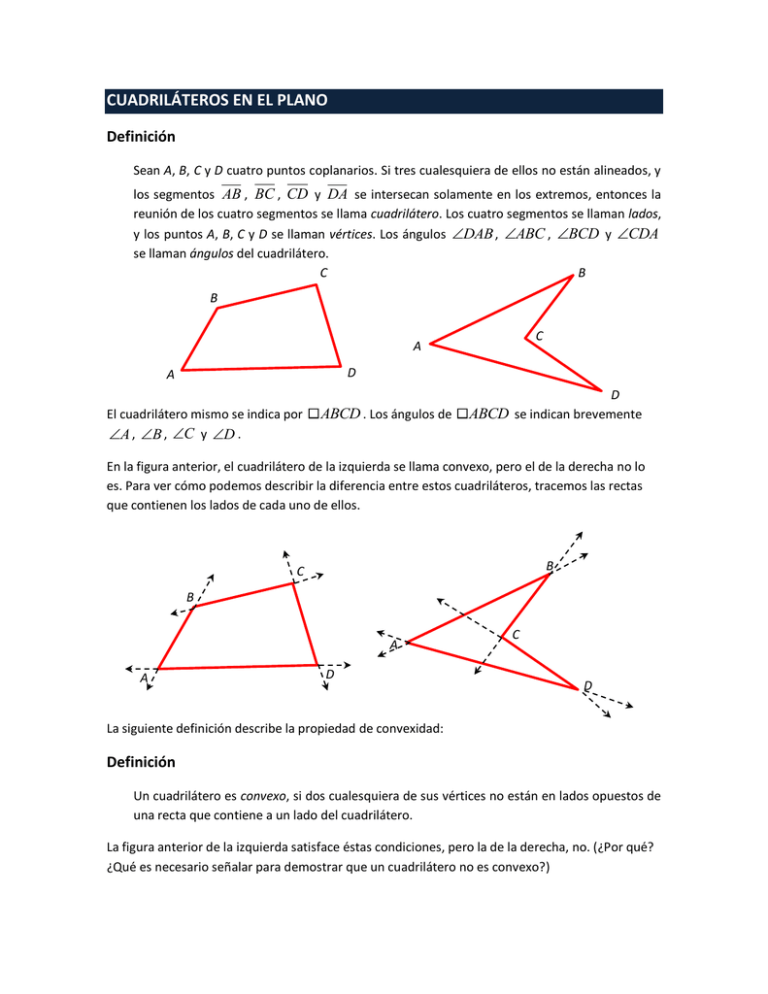
CUADRILÁTEROS EN EL PLANO
Definición
Sean A, B, C y D cuatro puntos coplanarios. Si tres cualesquiera de ellos no están alineados, y
los segmentos AB , BC , CD y DA se intersecan solamente en los extremos, entonces la
reunión de los cuatro segmentos se llama cuadrilátero. Los cuatro segmentos se llaman lados,
y los puntos A, B, C y D se llaman vértices. Los ángulos DAB , ABC , BCD y CDA
se llaman ángulos del cuadrilátero.
C
B
A
A
B
A
C
A
A
D
A
A
El cuadrilátero mismo se indica por
A , B , C y D .
ABCD . Los ángulos de
D
ABCD se indican brevemente
A
En la figura anterior, el cuadrilátero de la izquierda se llama convexo, pero el de la derecha no lo
es. Para ver cómo podemos describir la diferencia entre estos cuadriláteros, tracemos las rectas
que contienen los lados de cada uno de ellos.
B
A
B
A
C
A
A
A
D
A
C
A
D
A
La siguiente definición describe la propiedad de convexidad:
Definición
Un cuadrilátero es convexo, si dos cualesquiera de sus vértices no están en lados opuestos de
una recta que contiene a un lado del cuadrilátero.
La figura anterior de la izquierda satisface éstas condiciones, pero la de la derecha, no. (¿Por qué?
¿Qué es necesario señalar para demostrar que un cuadrilátero no es convexo?)
Definiciones
Dos lados de un cuadrilátero son opuestos, si no se intersecan. Dos ángulos son opuestos, si
no tienen común un lado del cuadrilátero. Dos lados son consecutivos, si tienen un extremo
común. Dos ángulos son consecutivos, si tienen común un lado del cuadrilátero. Una diagonal
de un cuadrilátero es un segmento determinado por dos vértices no consecutivos.
C
A
B
A
B
A
C
A
A
A
Así, en el
D
A
D
ABCD , los siguientes pares de lados y de ángulos son opuestos: AB y CD , ABC y
AD , A y C , B y D . Algunos de los pares consecutivos son: AB y BC , BC y CD ,
D y A , A y B . Las diagonales del
ABCD son AC y BD .
Definición
Un trapecio es un cuadrilátero que tiene dos lados paralelos.
B
A
A
B
A
C
A
D
A
A
C
A
D
A
Se observará que la definición permite la posibilidad de que ambos pares de lados opuestos sean
paralelos. Si esto sucede, tenemos un paralelogramo.
Definición
Un paralelogramo es un cuadrilátero en el cual ambos pares de lados opuestos son paralelos.
La demostración de los siguientes teoremas son directas:
Teorema
Cada diagonal descompone a un paralelogramo en dos triángulos congruentes.
Teorema
En un paralelogramo, dos lados opuestos cualesquiera son congruentes.
Corolario
Si dos rectas son paralelas, entonces todos los puntos de cada recta equidistan de la otra
recta.
Q
P
!
L1
!
L2
L1 L2
Recuérdese que la distancia de la distancia de un punto a una recta es la longitud del segmento
perpendicular desde el punto a la recta. Algunas veces, nos referimos al corolario anterior
diciendo que “las rectas paralelas equidistan en toda su extensión”.
Definición
La distancia entre dos rectas paralelas es la distancia de cualquier punto de una de ellas a la
otra.
Teorema
En un paralelogramo, dos ángulos opuestos cualesquiera son congruentes.
Teorema
En un paralelogramo, dos ángulos consecutivos cualesquiera son suplementarios.
Teorema
Las diagonales de un paralelogramo se bisecan.
Teorema
Si ambos pares de lados opuestos de un cuadrilátero son congruentes, entonces el
cuadrilátero es un paralelogramo.
Teorema
Si dos lados de un cuadrilátero son paralelos y congruentes, entonces el cuadrilátero es un
paralelogramo.
Teorema
Si las diagonales de un cuadrilátero se bisecan, entonces el cuadrilátero es un paralelogramo.
Teorema
El segmento entre los puntos medios de dos lados de un triángulo es paralelo al tercer lado y
tiene la mitad de su longitud.
B
E
D
C
A
DE AC
ROMBO, RECTÁNGULO Y CUADRADO
Definiciones
Un rombo es un paralelogramo cuyos lados son todos congruentes entre si.
Un rectángulo es un paralelogramo cuyos ángulos son todos rectos.
Un cuadrado es un rectángulo cuyos lados son todos congruentes entre sí.
D
A
C
B
D
A
C
D
C
B
A
B
Como anteriormente, se dejan al alumno las demostraciones de los siguientes teoremas:
Teorema
Si un paralelogramo tiene un ángulo recto, entonces tiene cuatro ángulos rectos y el
paralelogramo es un rectángulo.
Teorema
En un rombo, las diagonales son perpendiculares entre sí.
(Sugerencia: Ver el corolario 6-2.1 de su libro de texto.)
Teorema
Si las diagonales de un cuadrilátero se bisecan y son perpendiculares, entonces el cuadrilátero
es un rombo.