Respuesta a frecuencias altas para los BJT

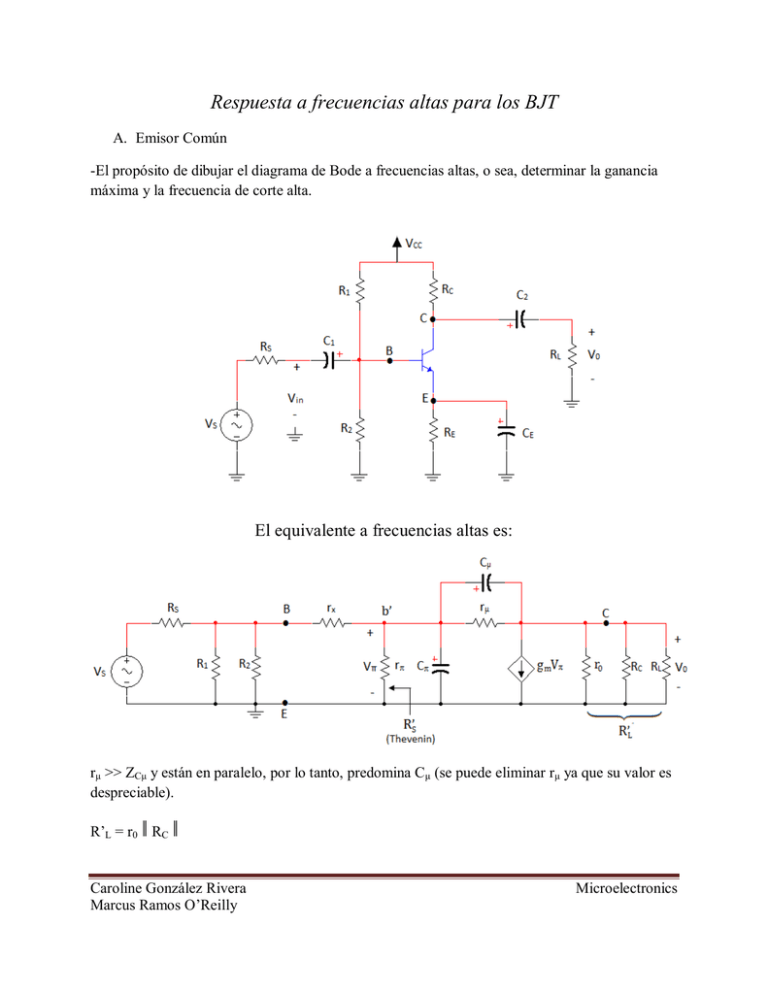
Respuesta a frecuencias altas para los BJT
A. Emisor Común
-El propósito de dibujar el diagrama de Bode a frecuencias altas, o sea, determinar la ganancia
máxima y la frecuencia de corte alta.
El equivalente a frecuencias altas es:
rμ >> ZCμ y están en paralelo, por lo tanto, predomina Cμ (se puede eliminar rμ ya que su valor es
despreciable).
R’L = r0 ǁ RC ǁ
Caroline González Rivera
Marcus Ramos O’Reilly
Microelectronics
-Aplico el teorema de Thevenin para determinar Req.(in).
Req.(in) = R’S = [ ( RS ǁ R1 ǁ R2 ) + rX ] ǁ rπ donde (R1
ǁ R2 = RB)
Equivalente AC aproximado y compacto a frecuencias altas:
Usando Miller:
CMin = Cμ (1 – AV)
CMout =
μ
Donde:
AV = AV midband =
gm =
π
∴ AV =
=
π
π
=
=
π
π
= -gm R’L
Ceq. in = Cπ + CMin = Cπ + Cμ
π
= Cπ + Cμ ( 1 + gmRL’ )
Ceq. out = CMout
Caroline González Rivera
Marcus Ramos O’Reilly
Microelectronics
fHin =
fHout =
π
π
*fC high sera la menor de las dos frecuencias.
B. Base Común
-Amplificador con un bandwidth amplio ya que no hay capacitancias parasíticas directas entre la
salida y la entrada.
Asumir r0 ≈ ∞
Equivalente AC a frecuencias altas:
Caroline González Rivera
Marcus Ramos O’Reilly
Microelectronics
-
rX es bien bajo ∴ es como si fuera corto circuito. ( b’ a ground)
-
r0 es bien alta en comparación con Rc y RL ∴ r0 → ∞ (open)
-
rμ es bien alto (MΩ) ∴ rμ → ∞ (open)
El equivalente aproximado es:
-Hay dos frecuencias de corte alta:
fH in =
π
fH out =
π
π
μ
Para determinar Req in visita desde Cπ (capacitor de entrada):
Req in =
= RTh
Caroline González Rivera
Marcus Ramos O’Reilly
Microelectronics
RP = RS ǁ RE ǁ rπ
Vπ = -Vtest
KCL:
Itest + gmVπ =
Itest + gm (-Vtest) =
Itest =
+ gm Vtest
Itest = Vtest
RTh = Req in =
=
= RP ǁ
Req in = RS ǁ RE ǁ rπ ǁ
Caroline González Rivera
Marcus Ramos O’Reilly
Microelectronics
Para determinar Req out vista desde Cμ (capacitor de salida):
Req out = RTh =
=
Itest = gm Vπ +
=
= R’L
Vπ = - ( gm Vπ ) RP ∴ Vπ = 0
Req out = R’L = RC ǁ RL
C. Colector Común
Caroline González Rivera
Marcus Ramos O’Reilly
Microelectronics
El equivalente AC a frecuencias altas es:
-rμ >> ZCμ (a frecuencias altas) ∴ predomina Cμ ( Cμ ǁ rμ )
-rμ es en orden de MΩ ∴ se puede reemplazar por un open
RL’ = r0 ǁ RE ǁ RL
RS’ = ( RS ǁ RB ) + rX
El equivalente aproximado es:
-Para buscar equivalentes de Miller hay que buscar la ganancia de B’ a E (donde esta Cπ).
-Notar que la corriente que pasa por rπ y Cπ es sumamente pequeña (es la corriente de base B’)
en comparación con la corriente (gm Vπ).
Caroline González Rivera
Marcus Ramos O’Reilly
Microelectronics
V0 = gm Vπ RL’
VB’ = Vπ + V0 = Vπ ( 1 + gm RL’
AV’b =
=
Aplicando Miller:
-En la entrada :
Ceq in = Cμ + Cπ ( 1 + AVb’ )
-La resistencia de entrada es:
Req in = RS’ ǁ
∴ fCin =
fC high = fC in
CMout =
RMout =
En la salida :
AV → +
AV ≈ 1 (colector común) ∴ CMout ≈ Cπ
≈0
-(Se puede despreciar este capacitor ya que en la salida es bien pequeño, no afecta el upper cutoff
frecuency).
Caroline González Rivera
Marcus Ramos O’Reilly
Microelectronics