2. Problema del Transporte.

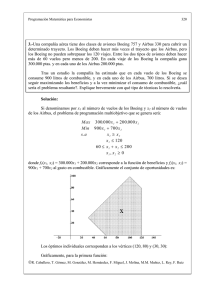
Programación Matemática para Economistas
2.- Problemas de transporte.
Supongamos que tenemos unidades de una mercancía situadas en m puntos de origen
distintos (centros de oferta) y hemos de transportarlas a n lugares de destino (centros de
demanda) para satisfacer necesidades de demanda. Se supone que se puede enviar
mercancía desde cualquier origen a cualquier destino y que el sistema está equilibrado, esto
es, el número total de unidades que se ofertan coincide con el total de unidades demandadas.
La cantidad de mercancía disponible en el origen i es ei y la cantidad que se demanda
en el destino j es dj. Dicho transporte ocasiona unos costes por unidad transportada que
dependen del lugar de origen y del de destino. El coste de transportar una unidad del origen
i al destino j es de cij unidades monetarias. Se desea conocer las unidades a transportar desde
cada origen a cada destino de manera que se minimice el coste total de transporte,
satisfaciendo las unidades demandadas de la mercancía en todos los destinos.
Sea xij el número de unidades de la mercancía que se transportan del origen i al
destino j, i = 1, 2, ..., m, j = 1, 2, ..., n.
Por la condición de equilibrio en el sistema (oferta total igual a demanda total)
tenemos que:
m
n
i =1
j =1
∑ ei = ∑ d j = k > 0.
Suponemos que:
(a) ei, dj, cij , xij son no negativas.
(b) La cantidad que se envía a cada destino no supera a la demanda en ese centro,
puesto que, en caso contrario, se incurriría en costes innecesarios; además se han de
satisfacer todas las demandas, luego:
m
∑x
i =1
ij
= d j , j = 1, 2, ..., n.
(c) A partir de (b) y, dado que la cantidad total enviada desde un origen no puede ser
mayor que la oferta de ese centro y que el sistema está equilibrado tenemos:
n
∑ xij = ei , i = 1, 2, ..., m.
j =1
Por tanto, el problema a resolver es:
R. Caballero, T. Gómez, M. González, M. Hernández, F. Miguel, J. Molina, M.M. Muñoz, L. Rey, F. Ruiz
Programación Matemática para Economistas
m
Min
n
∑ ∑ cij xij
i =1 j =1
n
s. a
∑x
j =1
ij
= ei
i = 1,2, ..., m
ij
= dj
j = 1,2, ..., n
m
∑x
i =1
que, expresado en forma matricial sería:
Min ct x
s.a A x = b
x≥0
donde c, b, x ∈ R
m+n
, A ∈ M (m+n)x(m⋅ n)
c = (c11, c12, ..., c1n, c21, c22, ..., c2n, ...., cm1, cm2, ..., cmn)t
b = (e1, e2, ..., em, d1, d2, ..., dn)t
x = (x11, x12, ..., x1n, x21, x22, ..., x2n, ...., xm1, xm2, ..., xmn)t
 1 1 ... 1 0

 0 0 ... 0 1

.........

 0 0 ... 0 0
A =
 1 0 ... 0 1

0 1 ... 0 0


.........

 0 0 ... 1 0
0
...
1
... 1
0
.........
0
...
0
0
...
0
1
...
0
.........
0
....
... 1
0
0
...
0
0
...
.........
1
....
...
1
1
0
...
0
1
...
.........
0
0
...
0 

0 


1

0

0



1 
Para resolverlo se puede utilizar cualquier algoritmo de los existentes para problemas
de programación lineal. Sin embargo, dado que el número de variables y de restricciones del
problema es grande, existen métodos de resolución propios para este problema.
Teorema 1.
Todo problema de transporte tiene una solución posible si ei y dj son finitos.
Demostración.
R. Caballero, T. Gómez, M. González, M. Hernández, F. Miguel, J. Molina, M.M. Muñoz, L. Rey, F. Ruiz
Programación Matemática para Economistas
Aplicamos el teorema de Weierstrass:
Se puede verificar que xij =
ei d j
es una solución factible al problema de transporte.
k
Cada xij está acotado por ei y dj, luego el conjunto de oportunidades es distinto del vacío y
está acotado.
La función objetivo es lineal y, por tanto, continua.
Tenemos asegurado que existe un máximo y un mínimo y, por consiguiente, el
problema de transporte siempre tiene solución.
Teorema 2.
La matriz A tiene rango m + n - 1
A partir del teorema 2 se tiene que una de las m + n ecuaciones del conjunto de
oportunidades es redundante, por lo que puede ser eliminada. Toda base para el problema de
transporte tendrá m + n - 1 vectores y, por tanto, toda solución admisible básica no
degenerada del problema tiene, a lo más, m + n - 1 variables positivas. Esto implica que, de
las m × n rutas existentes, en nuestro problema se enviarán mercancías por m + n - 1 de ellas
y ninguna por el resto, ya que deseamos minimizar costes.
Obtención de una solución admisible básica.
Para obtener una solución al problema de transporte construimos la siguiente tabla,
denominada tabla de flujos:
d1
d2
...
dj
...
dn
e1
x11
x12
...
x1j
...
x1n
e2
x21
x22
...
x2j
...
x2n
..
...
...
...
...
...
...
ei
xi1
xi2
...
xij
...
xin
..
...
...
...
...
...
...
em
xm1
xm2
...
xmj
...
xmn
Existen distintos métodos para obtener una solución admisible básica inicial al
problema de transporte. A continuación estudiamos dos de ellos.
R. Caballero, T. Gómez, M. González, M. Hernández, F. Miguel, J. Molina, M.M. Muñoz, L. Rey, F. Ruiz
Programación Matemática para Economistas
1.- Método de la esquina noroeste.
Se inicia el proceso asignando a la variable de la esquina noroeste, x11, un valor tal
que se sature el origen o el destino 1, es decir, x11 = min(d1, e1).
Si e1 ≤ d1 entonces x11 = e1 y x1j = 0, j = 2, 3, ..., n.
Si e1 ≥ d1 entonces x11 = d11 y xi1 = 0, i = 2, 3, ..., m.
A continuación hemos de determinar el valor de la variable que se encuentra en la
esquina noroeste.
Supongamos que e1 > d1, entonces x12 = min(d2, e1 - d1) y se completa con ceros el
resto de la fila o la columna correspondiente.
Si e1 < d1 entonces x21 = min(e2, d1 - e1)
Se elige de nuevo la variable que se encuentra en la esquina noroeste y se repite el
proceso hasta que se obtiene una solución.
La solución que se obtiene con este proceso es, por tanto, entera, y, dado que al
determinar cada xij se completa una fila o una columna con ceros, la solución posible
encontrada tiene, a lo más, m + n - 1 componentes distintas de cero.
Ejemplo:
Determine, mediante el método de la esquina noroeste, una solución al problema de
transporte representado por la siguiente tabla:
d1
d2
d3
d4
e1
x11
x12
x13
x14
5
e2
x21
x22
x23
x24
10
e3
x31
x32
x33
x34
15
4
8
12
6
Solución:
Paso 1: x11 = min(4, 5) = 4 ⇒ x11 = 4, x21 = x31 = 0, e1 = 5 - 4 = 1, d1 = 4 - 4 = 0 y
pasamos a x12
Paso 2: x12 = min(1, 8) = 1 ⇒ x12 = 1, x13 = x14 = 0, e1 = 1 - 1 = 0, d2= 8 - 1 = 7 y
pasamos a x22.
R. Caballero, T. Gómez, M. González, M. Hernández, F. Miguel, J. Molina, M.M. Muñoz, L. Rey, F. Ruiz
Programación Matemática para Economistas
Paso 3: x22 = min(10, 7) = 7 ⇒ x22 = 7, x32 = 0, d2 = 7 - 7 = 0, e2= 10 - 7 = 3 y
pasamos a x23.
Paso 4: x23 = min(3, 12) = 3 ⇒ x23 = 3, x24 = 0, d3 = 12 - 3 = 9, e2= 3 - 3 = 0 y
pasamos a x33.
Paso 5: x33 = min(15, 9) = 9 ⇒ x33 = 9, d3 = 9 - 9 = 0, e3 = 15 - 9 = 6 y pasamos a x34.
Paso 6: x34 = min(6, 6) = 6 ⇒ x34 = 6, d4 = 6 - 6 = 0, e3= 6 - 6 = 0.
Luego, la solución inicial es:
e1
d1
d2
4
1
7
e2
e3
e4
4
8
d3
d4
5
3
10
9
6
12
6
15
2.- Método de Vogel.
Este método se utiliza también para obtener una solución admisible básica no
degenerada. Posee la ventaja de que nos da una solución más cercana a la óptima que el
método de la esquina noroeste debido a que en la obtención de la solución intervienen los
costes de transporte de las mercancías.
Para obtener una solución por este método se siguen los siguientes pasos:
Paso 1: Determinar en cada línea de la tabla (fila o columna) la diferencia entre los
dos costes más pequeños y elegir la mayor de las m+n diferencias calculadas.
Paso 2: En la fila o columna en la que se tiene la mayor diferencia se elige la celda
con menor coste y se procede de manera similar a como hacíamos en el método de la
esquina noroeste:
xij = min(ei, dj)
y se modifica la oferta i-ésima (ei - xij ) o la demanda j-ésima (dj - xij). Desaparece una línea
y volvemos al paso 1.
Ejemplo:
Resolvemos el ejemplo anterior por el método de Vogel cuando los costes unitarios
de cada ruta son los que aparecen entre paréntesis en la siguiente tabla:
R. Caballero, T. Gómez, M. González, M. Hernández, F. Miguel, J. Molina, M.M. Muñoz, L. Rey, F. Ruiz
Programación Matemática para Economistas
d1
d2
d3
d4
e1
(2)
(7)
(9)
(3)
5
e2
(4)
(2)
(1)
(7)
10
e3
(6)
(8)
(9)
(3)
15
4
8
12
6
Calculamos las diferencias entre filas y columnas:
Dif. filas
Dif.
(2)
(7)
(9)
(3)
(1)
(4)
(2)
(1)
(7)
(1)
(6)
(8)
(9)
(3)
(3)
(2)
(5)
(8)
(0)
colum.
La mayor diferencia de línea es de 8, correspondiente a la columna 3. En ella el
menor coste es c23 = 1, luego:
d1
d2
d3
d4
(2)
(7)
(9)
(3)
5
e1
e2
(4)
(2)
(1)
(7)
0
0
10
0
(6)
(8)
(9)
(3)
0
15
e3
4
8
2
6
Calculamos nuevamente las diferencias de filas y columnas sin tener en cuenta la fila 2:
Dif. filas
Dif.
(2)
(7)
(9)
(3)
(1)
----
-----
----
----
----
(6)
(8)
(9)
(3)
(3)
(4)
(1)
(0)
(0)
colum.
R. Caballero, T. Gómez, M. González, M. Hernández, F. Miguel, J. Molina, M.M. Muñoz, L. Rey, F. Ruiz
Programación Matemática para Economistas
luego:
La mayor diferencia corresponde ahora a la columna 1 y el menor coste es c11=2,
e1
e2
e3
d1
d2
d3
d4
(2)
(7)
(9)
(3)
4
1
(4)
(2)
(1)
(7)
0
0
10
0
(6)
(8)
(9)
(3)
0
0
0
15
8
2
6
Calculando nuevamente las diferencias entre líneas tenemos:
Dif. filas
Dif.
---
(7)
(9)
(3)
(4)
----
-----
----
----
----
---
(8)
(9)
(3)
(5)
---
(1)
(0)
(0)
colum.
Puesto que la mayor diferencia corresponde a la fila 3, en la que el menor coste es
c34, luego:
e1
e2
e3
d1
d2
d3
d4
(2)
(7)
(9)
(3)
4
0
(4)
(2)
(1)
(7)
0
0
10
0
(6)
(8)
(9)
(3)
0
0
6
8
2
1
0
9
0
Calculamos las diferencias de costes en filas y columnas:
R. Caballero, T. Gómez, M. González, M. Hernández, F. Miguel, J. Molina, M.M. Muñoz, L. Rey, F. Ruiz
Programación Matemática para Economistas
Dif. filas
Dif.
---
(7)
(9)
---
(2)
----
----
----
----
----
---
(8)
(9)
---
(1)
---
(1)
(0)
---
Colum.
max(1,0, 2) = 2 correspondiente a la fila 1, en la que el menor coste es c12, luego:
e1
e2
e3
d1
d2
d3
d4
(2)
(7)
(9)
(3)
4
1
0
0
(4)
(2)
(1)
(7)
0
0
10
0
(6)
(8)
(9)
(3)
0
0
6
7
2
0
0
9
0
Completando la tabla, obtenemos la solución:
e1
e2
e3
d1
d2
d3
d4
(2)
(7)
(9)
(3)
4
1
0
0
(4)
(2)
(1)
(7)
0
0
10
0
(6)
(8)
(9)
(3)
0
7
2
6
0
0
0
0
0
0
0
Solución: x* = (4, 1, 0, 0, 0, 0, 10, 0, 0, 7, 2, 6).
Obtención de una solución óptima.
Dada una solución admisible básica, existen distintos algoritmos para pasar de ésta a
la solución óptima del problema. A continuación resolvemos un problema de transporte
R. Caballero, T. Gómez, M. González, M. Hernández, F. Miguel, J. Molina, M.M. Muñoz, L. Rey, F. Ruiz
Programación Matemática para Economistas
utilizando uno de ellos: el algoritmo de STEEPING-STONE, en el que se pasa de una
solución admisible básica a otra hasta llegar a la solución óptima.
Ejemplo:
Una empresa dispone de tres fábricas que producen el mismo bien. Las cantidades
disponibles de ese bien en cada fábrica es de 25, 35 y 30 unidades, respectivamente. La
empresa debe proveer a cuatro tiendas que demandan 10, 18, 20 y 42 unidades del producto,
respectivamente. Los costes unitarios de transporte del bien vienen dados por la siguiente
tabla:
d1
d2
d3
d4
e1
(3)
(2)
(5)
(4)
25
e2
(4)
(1)
(7)
(6 )
35
e3
(7)
(8)
(3)
(5)
30
10
18
20
42
90
Se desea determinar cómo han de realizarse los envíos a las tiendas de manera que se
minimice el coste total de transporte.
Aplicando el método de la esquina noroeste obtenemos la siguiente solución inicial:
e1
d1
d2
10
15
3
e2
d3
25
20
e3
10
18
d4
20
12
35
30
30
42
90
que es una solución no degenerada. El valor que alcanza la función objetivo para esta
solución es:
Z = 3⋅10 + 15⋅2 + 1⋅3 + 7⋅20 + 6⋅12 + 5⋅30 = 425
Para saber si esta solución es la óptima calculamos el coste marginal de transportar
una unidad de mercancía por cada una de las rutas que actualmente no se están utilizando.
Dicho coste marginal es lo que denominamos evaluador (Eij).
Supongamos que en nuestro ejemplo enviamos una unidad de mercancía por la
casilla (2, 1). Para mantener la estructura del problema hemos de restar una unidad de
mercancía de la casilla (1, 1), añadir una unidad a la casilla (1, 2) y quitar una unidad a la (2,
R. Caballero, T. Gómez, M. González, M. Hernández, F. Miguel, J. Molina, M.M. Muñoz, L. Rey, F. Ruiz
Programación Matemática para Economistas
2), lo que dará lugar a una variación (aumento o disminución) en el coste total de transporte
de :
E21 = 4 - 3 + 2 - 1 = 2
Dicha variación es lo que denominamos evaluador.
De igual forma podemos calcular los evaluadores para todas las casillas vacías en la
solución inicial:
E13 = 5 - 7 + 1 - 2 = -3
E14 = 4 - 6 - 2 + 1 = -3
E31 = 7 - 3 + 2 - 1 + 6 - 5 = 6
E32 = 8 - 1 + 6 - 5 = 8
E33 = 3 - 5 - 7 + 6 = -3
Teniendo en cuenta la interpretación de los evaluadores, observamos que el envío
de mercancías por las casillas (1, 3), (1, 4) y (3, 3) disminuye el coste de transporte. Por
tanto hemos de enviar mercancía por alguna de ellas. Dado que los tres E13 = E14 = E33,
elegimos cualquiera de ellos. En general habría que elegir el mayor en valor absoluto de
entre los negativos. Si todos los evaluadores fuesen positivos estaríamos ante la solución
óptima.
Una vez elegida la ruta por la que vamos a enviar mercancía, transportamos por ella
la mayor cantidad posible, de manera que se sigan satisfaciendo todas las demandas.
Eligiendo la casilla (1, 3) obtenemos una nueva solución en la que entra en la base la
variable x13 y sale x12:
d1
e1
d2
10
5
e3
10
d4
15
18
e2
d3
18
20
25
12
35
30
30
42
90
Calculamos de nuevo los evaluadores:
E12 = 2 - 5 - 1 + 7 = 3
E14 = 4 - 6 + 7 - 5 = 0
E21 = 4 - 7 + 5 - 3 = - 1
R. Caballero, T. Gómez, M. González, M. Hernández, F. Miguel, J. Molina, M.M. Muñoz, L. Rey, F. Ruiz
Programación Matemática para Economistas
E31 = 5 + 6 + 7 - 5 - 7 - 3 = 3
E32 = 8 + 6 - 5 - 1 = 8
E33 = 6 + 3 - 7 - 5 = -3
Entra x33:
d1
d2
e1
10
e2
0
18
e3
0
0
10
18
d3
d4
15
25
17
35
5
25
30
20
42
90
Los evaluadores serían en este caso:
E12 = 2 + 3 + 6 - 1 - 5 - 5 = 0
E14 = 4 + 3 - 5 - 5 = -3
E21 = 5 + 4 + 5 - 6 - 3 - 3 = 2
E23 = - 6 - 3 + 7 + 5 = 3
E31 = 7 + 5 - 3 - 3 = 6
E32 = 8 + 6 - 5 - 1 = 8
Entra x14:
d1
e1
d2
d3
10
15
25
17
35
20
10
30
20
42
90
18
e2
e3
10
18
d4
E12 = - 4 - 1 + 2 + 6 = 3
E13 = 5 + 5 - 4 - 3 = 3
E21 = 4 + 4 - 3 - 6 = -1
E23 = 7 + 5 - 6 - 3 = 3
E31 = 7 + 4 - 5 - 3 = 3
R. Caballero, T. Gómez, M. González, M. Hernández, F. Miguel, J. Molina, M.M. Muñoz, L. Rey, F. Ruiz
Programación Matemática para Economistas
E32 = 8 + 6 - 5 - 1 = 8
Luego, entra x21:
d1
d2
d3
25
25
7
35
20
10
30
20
42
90
e1
e2
10
18
e3
10
18
d4
E11 = 3 + 6 - 4 - 4 = 1
E12 = 2 + 6 - 4 - 1 = 3
E13 = 5 + 5 - 3 - 4 = 3
E23 = 7 + 5 - 6 - 3 = 3
E31 = 7 + 6 - 5 - 4 = 4
E32 = 8 + 6 - 5 - 1 = 8
Dado que todos los evaluadores son positivos ésta es la solución óptima al problema:
x* = (0, 0, 0, 25, 10, 18, 0, 7, 0, 0, 20, 10).
Si algún evaluador es igual a cero en la tabla óptima, entonces existe una solución
alternativa a la dada que da lugar al mismo coste de transporte, y que se obtendría
introduciendo esa variable en la base.
En caso de que no se cumpla la condición de equilibrio, es decir la cantidad
demandada total es mayor (menor) que la ofertada, se introducen en el problema centros de
oferta (demanda) ficticios, a los que se asocia un coste de transporte cero.
Si en el problema de transporte no es posible enviar mercancía desde cualquier
origen a cualquier destino, se asocia a esa ruta un coste de transporte infinito.
2.1.- Problemas de transbordo.
El problema de transbordo es un problema de transporte en el que se tienen centros
de oferta, centros de demanda y centros de transbordo.
Los centros de transbordo son centros que ofertan mercancía o la demandan y
pueden actuar como intermediarios en el transporte de mercancías entre los centros que
ofertan y los que demandan. El número de unidades para las que un centro de transbordo
R. Caballero, T. Gómez, M. González, M. Hernández, F. Miguel, J. Molina, M.M. Muñoz, L. Rey, F. Ruiz
Programación Matemática para Economistas
puede actuar como intermediario está limitado únicamente por el número de unidades que se
ofertan y demandan en el problema.
Además, se supone que la oferta total de mercancía (correspondiente a los centros de
oferta y a los centros de transbordo) es igual a la demanda total (de centros de demanda y de
centros de transbordo).
El transporte de unos centros a otros está restringido, en el sentido de que no es
posible transportar mercancías desde cualquier centro que oferte (ya sea centro de oferta o
de transbordo) a cualquiera que demande (ya sea centro de demanda o de transbordo).
El coste de transportar una unidad de mercancía depende del centro que la oferta y
del centro que la demanda.
Se desea saber el número de unidades a transportar de unos centros a otros de tal
forma que se minimice el coste total de transporte, satisfaciendo todas las demandas. Para
ello se plantea el problema como uno de transporte en el que:
1. Los centros de transbordo se consideran a la vez centros de oferta y centros de
demanda.
2. Se asigna un coste de transporte infinito en los siguientes casos:
• cuando no existe ruta para transportar mercancía de un centro a otro
• si el centro de oferta y de demanda es el mismo (esto ocurre para los
centros de transbordo, dado que se consideran a la vez como centros de
oferta y como centros de demanda).
En caso de que la cantidad total de mercancía ofertada sea mayor(menor) que la
demandada, se crean centros de demanda (oferta) ficticios, al igual que en el problema de
transporte.
Ejemplo:
Sea el problema de trasbordo definido por la siguiente figura:
R. Caballero, T. Gómez, M. González, M. Hernández, F. Miguel, J. Molina, M.M. Muñoz, L. Rey, F. Ruiz
Programación Matemática para Economistas
30 e1
6
1
d1 100
t1 40
40 e2
2
2
2
3
2
d2 20
t2 -65
1
3
2
7
d3 15
70 e3
2
2
5
5
d4 55
t3 20
60 e4
4
6
d5 30
El problema de transporte que lo resuelve viene dado por la siguiente tabla. Dado
que la suma de demanda total es mayor que la oferta total, se ha introducido un centro de
oferta ficticio (e5), que oferta 25 unidades de mercancía (la diferencia entre la demanda total
y la oferta total). Asociado a ese centro de oferta va un coste infinito (M), así como a todas
las rutas por las que no se puede transportar mercancía. Los centros de transbordo aparecen
a la vez como centros de oferta y de demanda. Si el centro de transbordo es de oferta
(demanda) cuando aparece como centro de demanda (oferta) la cantidad que demanda este
centro es el opuesto de la cantidad que oferte.
e1
e2
e3
e4
e5
t1
t2
t3
d1
d2
d3
d4
d5
t1
t2
t3
(6)
(M)
(M)
(M)
(M)
(1)
(M)
(M)
(M)
(M)
(M)
(M)
(M)
(2)
(M)
(M)
(M)
(M)
(7)
(M)
(M)
(2)
(1)
(M)
(M)
(M)
(M)
(M)
(6)
(M)
(2)
(5)
(M)
(M)
(M)
(M)
(M)
(M)
(M)
(M)
(M)
(3)
(2)
(M)
(M)
(M)
(M)
(M)
(3)
(M)
(M)
(M)
(6)
(2)
(M)
(M)
(M)
(M)
(M)
(5)
(4)
(M)
(2)
(M)
100
20
15
55
30
-40
65
-20
30
40
70
60
25
40
-65
20
R. Caballero, T. Gómez, M. González, M. Hernández, F. Miguel, J. Molina, M.M. Muñoz, L. Rey, F. Ruiz