3. Potencial Eléctrico

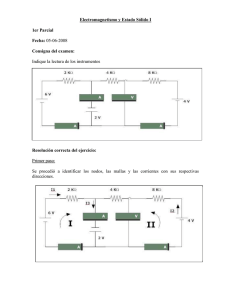
Física. 5º Año
Lcdo. Eleazar J. García
Potencial Eléctrico y Diferencia de Potencial
Potencial Eléctrico: se llama potencial eléctrico en un punto A de un campo eléctrico al trabajo
(W) necesario para transportar la unidad de carga positiva (q0) desde fuera del campo hasta dicho
punto.
Escribiéndolo en una ecuación tenemos que:
W
VA 
q0
Nota: “la carga positiva (q0) es llamada carga móvil o
carga de prueba”
Unidad del Potencial en el Sistema M.K.S.: en éste sistema la unidad de trabajo (W) es el Joule, la
de carga eléctrica (q0) es el Coulomb y la unidad potencial eléctrico (V) es el Voltio, siendo:
Joule
1Voltio  1
Coulomb
Potencial debido a una carga puntual: el potencial eléctrico debido a una carga puntual q, situada
a una distancia r de un punto P (donde se supone ubicada q0), puede calcularse mediante la
ecuación:
q
VP  K
r
Diferencial de Potencial: se llama diferencia de potencial entre dos puntos A y B de un campo
eléctrico al trabajo que tiene que realizar un agente externo para llevar la unidad de carga positiva
desde A hasta B.
De acuerdo con la definición de diferencia de potencial podemos escribir:
W
VAB  VB  VA  AB
q0
Si se abandona una carga positiva en B, es
repelida por la que crea el campo, tendiendo a
moverse hacia A. De esta manera las cargas
positivas tienden a caer de mayor a menor
potencial, gastando su energía potencial.
Para calcular el potencial eléctrico resultante que
produce un grupo de cargas puntuales en un
punto dado, calculamos por separado cada una
de los potenciales y luego se suman
algebraicamente.
1
Física. 5º Año
Lcdo. Eleazar J. García
Energía Potencial Eléctrica: consideremos dos cargas eléctricas q1 y q2, las cuales están separadas
entre sí una distancia r, como lo muestra la figura.
Si las cargas son de signos opuestas y deseamos aumentar la separación entre ellas se debe
realizar un trabajo positivo, en cambio si las cargas son del mismo signo se debe realizar un trabajo
negativo.
“La energía potencial eléctrica de un sistema de cargas puntuales es el trabajo necesario para
trasladar las cargas desde una separación infinita hasta sus posiciones finales sin aceleración”.
La energía potencial eléctrica del sistema de dos cargas (q1 y q2), se calcula mediante:
q q
U12  k 1 2
r
Para calcular la energía potencial eléctrica de un sistema de más de dos cargas, se calcula por
separado la energía de cada par y se suman los resultados algebraicamente. Por ejemplo, si el
sistema de cargas está formado por q1, q2 y q3, entonces, U = U12 + U13 + U23, donde U es la energía
potencial eléctrica del sistema.
Ejemplo:
Las cargas: qc  5  106 C, qD  3  106 C
y
qE  2  106 C, están colocadas en los vértices C, D y E
de la figura adjunta. Calcular: VA, VB y VAB. ¿Cuál es el
trabajo necesario para transportar la carga
q0  4  106 C desde B hasta A y la energía potencial
eléctrica del sistema?
Solución:
Calculemos el potencial eléctrico resultante en A:
En efecto; VA=Vc+VD+VE
6
qc
N  m2  5  10 C 
 9  109 2 
rAC
C
3m
VC  15000Volts
VC  K
2
3  106 C 

qD
9 Nm
VD  K  9  10

rAD
C2
3m
VD  9000Volts
Luego, el potencial eléctrico resultante en es:
2
2  106 C 

qE
9 Nm
VE  K  9  10

rAE
C2
3m
VE  6000Volts
2
Física. 5º Año
Lcdo. Eleazar J. García
VA  15000 Volts  9000 Volts  6000 Volts
VA  0 Volts
Calculemos el potencial eléctrico resultante en el punto B:
En efecto, VB=VC+VD+VE
2
5  106 C 

qc
9 Nm
VC  K  9  10

rBC
C2
6m
VC  7500Volts
Antes de calcular VD y VE debemos calcular las distancias rBD y rBE. Observe que rBD = rBE.
Apliquemos el Teorema de Pitágoras:
rBD    3m   3m
2
2
2
 rBD  9m2  9m2  18m2  4,24m
2
3  106 C 

qD
9 Nm
VD  K  9  10

rBD
C2
4,24m
VD  6345Volts
q
N  m2  2  10 C 
VE  K E  9  109 2 
rAE
C
4,24m
VE  4245Volts
6
Entonces, el potencial resultante en B es:
VB  7500 Volts  6345Volts  4245Volts
VB  3113Volts
Calculemos VB – VA:
VB – VA = 3113 Volts – 0 Volts = 3113 Volts
Calculemos el trabajo necesario para transportar a la carga q0 desde B hasta A:
Debemos aplicar la ecuación siguiente:
W
VA  VB  BA  WBA  q0  VA  VB 
q0
WBA  4  106 C  0 Volts  3113Volts 
WBA  0,012524 Joules
Calculemos U:
Como tenemos tres cargas, entonces: U = UCD + UCE + UDE
2
5  106 C  3  106 C 

qC  qD
9 Nm
UCD  K
 9  10

 0,032 Joules
rCD
C2
4,24m
UCE  K
6
6
qC  qE
N  m2  5  10 C  2  10 C 
 9  109 2 
 0,021 Joules
rCE
C
4,24m
3
Física. 5º Año
Lcdo. Eleazar J. García
2
3  106 C  2  106 C 

qD  qE
9 Nm
UDE  K
 9  10

 0,009 Joules
rDE
C2
6m
Por lo tanto:
U = - 0,032 Joules - 0,021 Joules + 0,009 Joules = - 0,044 Joules.
EJERCICIOS.
1. Determinar el valor del potencial eléctrico creado por una carga puntual q1=12 · 10-9 C en
un punto ubicado a 10 cm del mismo como indica la figura
2. Dos cargas puntuales q1=12 · 10-9 C y q2=-12 · 10 -9 C están separadas 10 cm, como muestra
la figura. Calcular las diferencias de potenciales VAB, VBC y VAC.
3.
Determine el potencial eléctrico a 9 cm de un cuerpo puntual cuya carga eléctrica es de
-9 μC.
4. En los extremos de la hipotenusa de un triángulo rectángulo se encuentran dos cargas
eléctricas q1  4  108 C y q2  3  108 C, separadas 10 cm. Un punto B situado en el
vértice del ángulo recto está a 8 cm de q1 y a 6 cm de q2.
Calcular:
a) El potencial eléctrico en un punto A sobre la hipotenusa y equidistante de las
cargas.
b) El potencial en el punto B.
c) El trabajo necesario para transportar una carga de 2,5 · 10 -8 C desde B hasta A.
d) La energía potencial eléctrica del sistema.
5. En la figura se muestran tres cargas q1  2  106 C, q2  2  106 C y q3  2  106 C. ¿Cuál
es la energía potencial eléctrica de las tres cargas?
4
Física. 5º Año
Lcdo. Eleazar J. García
6. Una partícula cuya carga eléctrica es de +2 μC está ubicada en el origen de un sistema de
coordenadas cuyas dimensiones son centímetros. Un segundo cuerpo puntual es ubicado
en el punto (100, 0). Si su carga eléctrica es de -3 μC. ¿En qué punto del eje x el potencial
eléctrico es nulo?
5