Semana 2 Función logarítmica (parte 1)

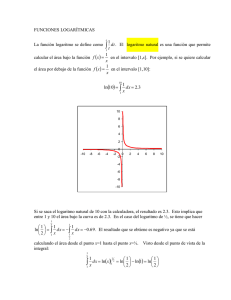
Semana
Semana
22
Función logarítmica (parte 1)
Función logarítmica (parte 1)
¡Empecemos!
Esta semana estudiaremos los
logaritmos y sus propiedades
más importantes. Discutiremos
acerca del concepto de logaritmo y varias formas de calcularlo, además de buscar la
solución a situaciones de la
vida real. Esto nos conducirá a
estudiar las propiedades de los
logaritmos y ver cómo éstos
facilitan el cálculo de operaciones combinadas (más complejas). Durante la lectura del material encontrarás preguntas y planteamientos interesantes que te permitirán comprender
mejor el tema.
¿Qué sabes de...?
Intenta hallar el exponente de las siguientes expresiones (ecuaciones exponenciales). ¡Has uso de tus saberes en cuanto a la potencia!
a) 2x = 8
b) 3z = 1/9
c) 4x = 64
d) 10 y = 10000
Puedes preguntarte, por ejemplo, ¿cuántas veces se debe multiplicar el 2
para obtener el resultado 8 (la potencia)? Así obtendrás el exponente x.
El reto es...
Los logaritmos son utilizados como una herramienta para modelar y explicar fenómenos de la naturaleza. Veamos la siguiente aplicación:
Las bacterias de un recipiente de 4 litros se duplican cada minuto. Después
de 60min el recipiente está lleno. ¿Cuánto tiempo pasó hasta que se llenó la mitad del recipiente? ¡Pendiente: el recipiente no se llena a los 30min! Entonces,
¿qué operación podemos hacer para encontrar el tiempo que tarda?
184
La condición que nos permite entender la situación se centra en la forma
cómo se reproducen las bacterias. Si inicialmente hay una bacteria, después
de un minuto hay dos bacterias, en el siguiente minuto hay cuatro bacterias
Semana 2
Función logarítmica (parte 1)
y así sucesivamente, vemos que se reproducen por minuto de la siguiente
manera: 1, 2, 4, 8, 16, 32… que es una potencia de base 2, ya que 20= 1, 21= 2,
22=4, 23=8, 24=16, 25= 32… Expresamos simbólicamente 2tiempo = número de
bacterias, es decir, 2t= N.
Vamos al grano
Para resolver el problema de las bacterias, comprendamos la definición de
los logaritmos:
Dado un número real a positivo (a > 0), no nulo (a ≠ 0) y distinto de 1 (a
≠ 1), y un número x positivo y no nulo (x > 0; x ≠ 0), se llama logaritmo
en base a de x al exponente y al que hay que elevar dicha base para
obtener el número.
Para indicar que y es el logaritmo en base a de x se escribe:
loga X = y
Se lee «logaritmo en base a de x es igual a y».
En base a lo anterior podemos decir que loga X = y (notación logarítmica) equivale a decir x = ay (notación exponencial). Usemos la definición de logaritmos para dar respuesta a la situación 1 (ver figura 4).
Pulsar teclas (mantener orden)
Pantalla (DEG)
2^60
1,152921505x1018
Figura 4
Usemos la expresión 2t= N y la calculadora para saber cuántas bacterias hay
a los 60min. Observamos que el número de bacterias es 1,152921505x1018. La
pregunta que se hace en la situación 1 es cuánto tiempo pasó hasta que se llenó la mitad del recipiente. Para ello debemos saber qué cantidad de bacterias
185
Semana 2
Función logarítmica (parte 1)
hay cuando esté por la mitad. Así que hacemos la división 1,152921505x1018/2
y resulta que: 5,764607523x1017.
Si utilizamos la expresión 2t= N, escribimos que 2t = 5,764607523x1017¿Cuál
es el valor de t? Según la definición de logaritmo 2t = 5,764607523x1017 es
equivalente a escribir log2 5,764607523x1017 = t ¿Por qué?
Usemos la calculadora para obtener el valor de t. El resultado es 59min. Esto
se debe a que en el próximo minuto la mitad de bacterias se reproduce y llena
de manera completa el recipiente.
Pulsar teclas (mantener orden)
Pantalla (Math-Deg)
log2 5,764607523<1017
59
Figura 5
Es importante resaltar que la base de los logaritmos puede ser cualquier
número real positivo y distinto de 1 (a>0; a ≠ 1). En este sentido, no siempre
podemos obtener de manera manual el logaritmo de un número. Las bases
logarítmicas más usadas en matemática son los logaritmos de base 10 y e
(número de euler). Simbólicamente escribimos: log10 x = log x (Base 10) y loge
x = ln x (Base e).
Los logaritmos cumplen con ciertas propiedades que nos permiten calcular
de forma sencilla cuando se quiere obtener el logaritmo de operaciones combinadas (productos, divisiones, potencias y raíces). Veamos en la tabla 1 las
propiedades de los logaritmos.
Tabla 1
1. Logaritmos de un producto
Expresión simbólica
loga x - y = loga x + loga y
186
Interpretación
El logaritmo a base de a de una
multiplicación (x · y) resulta ser
igual a la suma del logaritmo de
base a del primer factor (x) más el
logaritmo de base a del segundo
factor (y). En el otro sentido también se cumple la propiedad.
Semana 2
Función logarítmica (parte 1)
2. Logaritmos de un cociente
Expresión simbólica
Interpretación
El logaritmo a base de a de una
división (x ÷ y) resulta ser igual
a la resta del logaritmo de base
a del primer factor (x) menos el
logaritmo de base a del segundo
factor (y). En el otro sentido también se cumple la propiedad.
x
= loga x - loga y
y
loga
3. Logaritmo de una potencia
Expresión simbólica
Interpretación
El logaritmo a base de a de una
potencia (xn) resulta ser igual al
producto del exponente (n) por
el logaritmo de base a del número (x). En el otro sentido también
se cumple la propiedad.
loga xn = n · loga x
4. Logaritmo de una potencia
Expresión simbólica
loga
a
x =
Interpretación
El logaritmo a base de a de una
raíz (a x) resulta ser igual a la división del logaritmo de base a del
número (x) entre el índice (n). En
el otro sentido también se cumple la propiedad.
loga x
n
Para que comprendamos mejor las propiedades, analicemos los siguientes
ejemplos: Dados los logaritmos logb 10 = 8, logb 7 = 2 y logb 6 = 15 calcula los
logaritmos siguientes usando las propiedades:
a) logb (10 · 6)
b) logb
7
6
c) logb 103
d) logb
4
7
187
Semana 2
Función logarítmica (parte 1)
Solución (a): Para encontrar la respuesta correcta, notemos que logb 10 = 8
y logb 6 = 15. Planteamos el ejercicio:
logb (10 · 6) = logb 10 + logb 6
Por la propiedad (1) de los logaritmos
= 8 + 15
Sustituimos los valores de logb 10 + logb 6
= 23
Sumando los resultados
Respuesta: logb (10 · 6) = 23
Solución (d): Para encontrar la respuesta correcta, notemos que logb 7 = 2.
Planteamos el ejercicio:
logb 7
= 4
2
= 4
1
= 2
1
Respuesta: logb 4 7 =
2
logb
4
7
Por la propiedad (4) de los logaritmos
Sustituimos los valores de logb 7
Simplificando la fracción
Toma como ejemplos ilustrativos las soluciones mostradas y realiza con tus
compañeros del CCA los ejercicios (b) y (c). Es importante que justifiques los
pasos que hagas como, por ejemplo, la propiedad que estás usando y qué
operaciones estás haciendo.
Para saber más…
Para determinar la magnitud de un sismo en la escala de Richter (ver
tabla 2) se emplea una función logarítmica de base 10 y los datos que
aporta el sismógrafo. La función logarítmica es la siguiente:
Magnitud R = log10 (
a
)+B
T
En donde a designa la amplitud del terremoto registrado en la estación
sismológica (en micras), T es el período de la onda sísmica (en segundos) y B es un factor empírico que indica el debilitamiento al aumentar
la distancia al epicentro del terremoto.
188
Semana 2
Función logarítmica (parte 1)
Tabla 2
Magnitud en escala de Richter
Efecto del terremoto
Menos de 3.5
Generalmente no se siente,
pero es registrado.
3.5 - 5.4
A menudo se siente, pero
solo causa daños menores.
5.5 - 6.0
Ocasiona daños ligeros a
edificios.
6.1 - 6.9
Puede ocasionar daños severos en áreas muy poblada.
7.1 - 7.9
Terremoto mayor. Causa graves daños.
8 o mayor
Gran terremoto. Destrucción
total de comunidades
cercanas.
Los efectos de los terremotos dependen de la magnitud con la cual
se hayan producido.
Situación 1: supongamos que ha ocurrido un movimiento telúrico cuyo
epicentro está a 500km de la estación sismológica que se encuentra en
el Observatorio Juan Manuel Cajigal y que los sismógrafos registraron
una amplitud de 10 micras y un período de la onda sísmica de 1seg.
Sabiendo que la constante B es igual a 6,8:
a) Calcula la magnitud del movimiento.
b) Identifica cómo se cataloga un movimiento telúrico de tal intensidad.
189
Semana 2
Función logarítmica (parte 1)
Solución: Tomando en cuenta el ejemplo anterior que trataba sobre los
terremotos, obtenemos los datos: a =10 micras; T =1seg y B = 6,8.
Empleemos la fórmula: Magnitud R = log10 (
a
)+B
T
Sustituyendo los valores de a, T y B escribimos la expresión como sigue:
Para obtener el resultado de la expresión busca una calculadora científica que posea logaritmos de base 10 y marca como se muestra en la figura 6. El terremoto posee una magnitud de R= 7,8 en la escala de Richter,
lo que indica que el sismo tiene un efecto que causa graves daños en la
población de Juan Manuel Cajigal.
Pulsar teclas (mantener orden)
Pantalla (Math-Deg)
log ( 10 ) + 6,8
I
7,8
Figura 6
Para ver un video ilustrativo sobre el uso de la definición de los logaritmos, haz clic en: http://goo.gl/NLkNi
Observa una presentación que explica de una manera muy sencilla las
propiedades de los logaritmos, disponible en: http://goo.gl/gLT3q
Aplica tus saberes
1. Calcula los logaritmos:
190
a) log2 64
d) log5 625
b) log4 16
e) log 1000
c) log3
1
81
Función logarítmica (parte 1)
Semana 2
2. Supongamos que ha ocurrido un movimiento telúrico cuyo epicentro
está a 200km de la estación sismológica que se encuentra en el Observatorio de Boconó en el estado Trujillo y que los sismógrafos registraron
una amplitud de 8 micras y un período de la onda sísmica de 1seg. Sabiendo que la constante B es igual a 4,8:
a) Calcula la magnitud del movimiento.
b) Identifica cómo se cataloga un movimiento telúrico de tal intensidad.
3. Dados los logaritmos: loga 23 =10, loga 11 =100 y loga 6 = 9, calcula los
logaritmos siguientes usando las propiedades.
a) loga 11
6
b) loga (23 ·9)
c) loga 11-4
d) loga
3
9
Comprobemos y demostremos que…
1. Encuentra con tus compañeros las soluciones a los problemas y ejercicios propuestos y consulta con tu facilitador las dudas que tengas.
2. Reflexiona sobre tus aprendizajes:
a) ¿Cómo contribuyeron mis saberes previos a la realización de las
actividades?
b) ¿Qué de nuevo aprendí en este proceso de aprendizaje?
c) ¿En qué parte de las actividades tuve problemas de comprensión?
d) ¿Qué proceso seguí para desarrollar eficazmente las actividades?
191