Taller de Estadistica - UNIVERSIDAD DISTRITAL FRANCISCO

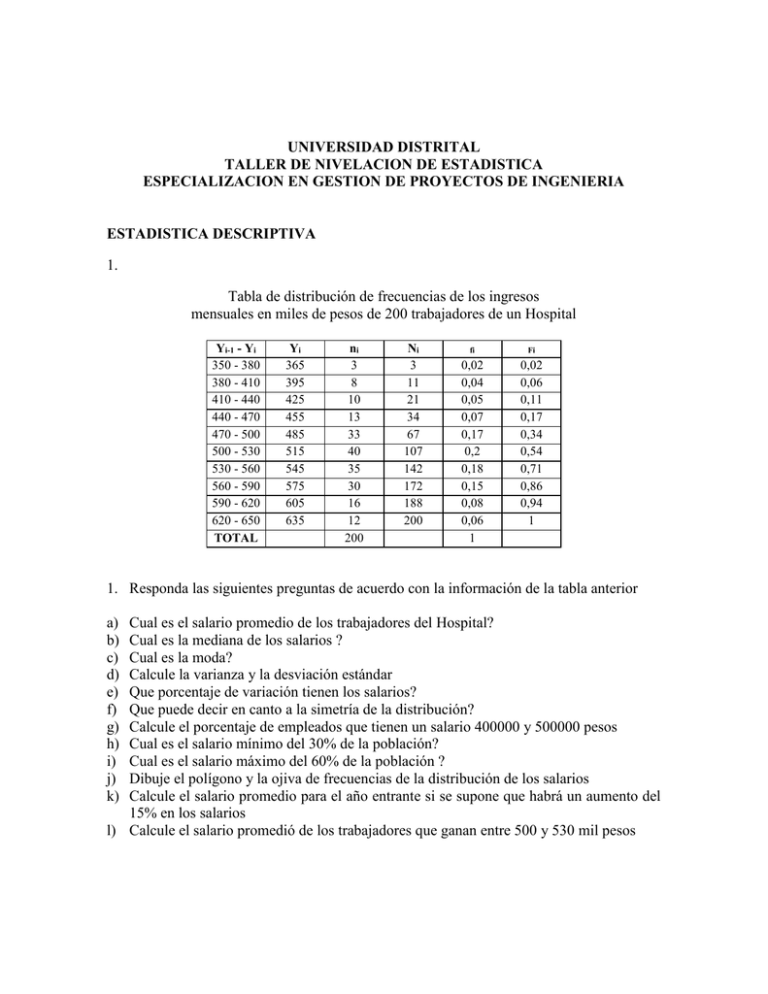
UNIVERSIDAD DISTRITAL
TALLER DE NIVELACION DE ESTADISTICA
ESPECIALIZACION EN GESTION DE PROYECTOS DE INGENIERIA
ESTADISTICA DESCRIPTIVA
1.
Tabla de distribución de frecuencias de los ingresos
mensuales en miles de pesos de 200 trabajadores de un Hospital
Yi-1 - Yi
350 - 380
380 - 410
410 - 440
440 - 470
470 - 500
500 - 530
530 - 560
560 - 590
590 - 620
620 - 650
TOTAL
Yi
365
395
425
455
485
515
545
575
605
635
ni
3
8
10
13
33
40
35
30
16
12
200
Ni
3
11
21
34
67
107
142
172
188
200
fi
Fi
0,02
0,04
0,05
0,07
0,17
0,2
0,18
0,15
0,08
0,06
1
0,02
0,06
0,11
0,17
0,34
0,54
0,71
0,86
0,94
1
1. Responda las siguientes preguntas de acuerdo con la información de la tabla anterior
a)
b)
c)
d)
e)
f)
g)
h)
i)
j)
k)
Cual es el salario promedio de los trabajadores del Hospital?
Cual es la mediana de los salarios ?
Cual es la moda?
Calcule la varianza y la desviación estándar
Que porcentaje de variación tienen los salarios?
Que puede decir en canto a la simetría de la distribución?
Calcule el porcentaje de empleados que tienen un salario 400000 y 500000 pesos
Cual es el salario mínimo del 30% de la población?
Cual es el salario máximo del 60% de la población ?
Dibuje el polígono y la ojiva de frecuencias de la distribución de los salarios
Calcule el salario promedio para el año entrante si se supone que habrá un aumento del
15% en los salarios
l) Calcule el salario promedió de los trabajadores que ganan entre 500 y 530 mil pesos
2. En una encuesta que se realizo en un colegio, se indago a 54 estudiantes por el numero
de horas en la semana en las que había visto televisión, los resultados fueron tabulados
en 7 clases cuyos resultados fueron los siguientes: 3 estudiantes entre 0 y 10 , 8 entre 10
y 20 , 12 entre 20 y 30 ,16 entre 30 y 40 , 9 entre 40 y 50 y 2 entre 60 y 70 horas
semanales respectivamente. Construya la tabla , el hitograma y la ojiva de la
distribución de frecuencias del numero de horas en que los estudiantes ven televisión a
la semana
3. En el ejercicio anterior, si X es la variable que cuenta el numero de horas a la semana
en que los estudiantes ven televisión calcular:
a. X Sx Sx C(x) y la mediana de los datos
b. Que porcentaje de los estudiantes ven televisión entre 12 y 43 horas a la semana
c. Que porcentaje de los estudiantes ven por lo menos 20 horas televisión a la semana
d. Cual es el mayor numero de horas semanales que ven el 70% de los estudiantes
e. De tres conclusiones del comportamiento de los estudiantes respecto a la televisión
PROBABILIDADES
4. En un depósito hay almacenados 5050 equipos de televisión. En la siguiente tabla se
muestran como están clasificados de acuerdo a su marcar y modelo:
Modelo
S1
S2
S3
S4
Total
B1
700
650
450
500
2300
MARCA
B2
B3
225
500
175
400
350
325
175
600
925
1825
Total
1425
1225
1125
1275
5050
De acuerdo con los datos de la tabla calcular:
a) P(B1),
P(S4  B2),
P(S4  B2)
P(S3  B1)
b) La probabilidad de que un equipo seleccionado al azar sea de marca B1 dado que su
modelo es S4.
c) La probabilidad de que el equipo seleccionado sea de modelo S2 y de marca B3.
d) La probabilidad de que un equipos seleccionado sea de marca B1 o B3
5. Sea P(A) = 0.6 , P(A  B) = 0.25 P(B) = 0.7 Calcular,.
P( A  B) , P(A) , P(A B) , P(A - B) , Son A y B eventos independientes ? justifique su
respuesta
6. En una ciudad grande el 70% de los hogares compra un periódico matutino, el 90% uno
vespertino, suponga que los eventos son independientes que probabilidad hay de que en un
hogar escogido al azar compren ambos periódicos.
7. Tres industrias manufactureras suministran microprocesadores a un fabricante de equipos
de telemetría, donde se sabe que el fabricante1 suministra el 15% y en el cual se sabe que
produce el 2% de defectuosos, el fabricante 2 suministra el 80% y se sabe que la
producción de defectuosos es del 1%, y el fabricante 3 suministra e 5% y su producción de
defectuosos es del 3%. Si un equipo de telemetría tiene un procesador defectuoso, calcular :
a) la probabilidad de que lo halla producido el proveedor 1
b) la probabilidad de que lo halla producido el proveedor 2
c) la probabilidad de que lo halla producido el proveedor 3
8. Una oficina de compras va a asignar un contrato para papel de computadora y otro para
discos de microcomputadora a alguna de las tres empresas que concursan para estos
contratos. Cualquier empresa podría recibir ambos contratos. Calcular la probabilidad de
que:
a. la empresa 1 reciba un contrato si es que los dos contratos no se asignan a la misma
empresa
b. la empresa 1 reciba ambos contratos
c. la empresa 1 reciba el contrato de papel dado que no recibió el de discos
FUNCIONES DE DISTRIBUCION
9. La probabilidad de que un individuo acierte, en un solo tiro, Con un dardo en el centro
de un blanco es 0.40. Lanza l0 dardos consecutivamente . hallar la probabilidad de que de
en el blanco:
a. Todas las 10 veces
b. 5 veces.
c. Entre 7 y l0 veces inclusive.
d. Menos de tres veces.
10 Suponga que una variable aleatoria x tiene como función de densidad de probabilidad
definida por :
kx(1- x) si
0x 1
f(x) =
0
en otro caso
a. Calcule el valor de k
b. Calcule E(x) y V(x)
c. Calcule F(x)
d. Calcule P( x  0.4  x  0.8 )
11. Los tiempos de servicio en una ventanilla de un cajero de un banco sigue una
distribución exponencial con promedio 3.2 minutos. Un cliente va a la ventanilla a las
4:00 p.m.
a. Calcule la probabilidad de que el cliente este todavía allí a las 4:02 p.m
b. Calcule la probabilidad de que todavía este allí a las 4:04 dado que estaba allí a las 4:02
12. La cantidad semanal que una compañía gasta en mantenimiento y reparaciones sigue
una distribución normal con media $400 y una desviación estándar de $20. Si el
presupuesto para cubrir los gastos de reparación para la semana siguiente es de $450.
a. Cual es la probabilidad que los costos reales sobrepasen la cantidad presupuestada
b. Cuanto debe ser el presupuesto semanal para gastos y reparaciones para que tan solo re
rebase con una probabilidad del 0.1
13. Cuando deja de funcionar una tarjeta de circuito de un integrado, un sistema de
computo se detiene hasta que se entregue una tarjeta nueva . El tiempo de entrega X
uniformemente distribuido en un intervalo de uno a cinco días. El costo C de la falla lo
constituye el costo fijo de reparación CR y un costo que crece directamente proporcional
al cuadrado del tiempo de entrega es decir C = CR + kX2 , donde k es la constante de
proporcionalidad.
a. Calcule la probabilidad que el tiempo de entrega sea de dos días o mas
b. Calcule el costo esperado en términos de k y CR
16. Un 35% de los internos de una institución correccional son reincidentes. Se selecciona,
para una evaluación, una muestra aleatoria de l5 internos.
a. Hallar la probabilidad de que el número de reincidentes del grupo sea mayor que l0.
b. Hallar la probabilidad de que cinco o más sean reincidentes.
17. En un sector del país los gastos semanales de alimentación de una familia están más o
menos normalmente distribuidos, con media y desviación típica de US$ 60 y US$ 50
respectivamente.
a. Hallar la proporción de familias que gastan en alimentos más de US$ 80 por semana.
b. Hallar la proporción de los que gastan menos de US$ 50 por semana.
18. Supongase que se sabe que la probabilidad de recuperación de cierta enfermedad es del
40%. Si l5 personas contraen la enfermedad cual es la probabilidad de que:
a. 3 o más se recuperen
b. Menos de 3 se recuperen
c. Se recuperen entre 4 y l0 inclusive.
19. Supóngase que durante un periodo de varios años, es número promedio de muertes
debidas a ciertas enfermedad no contagiosa ha sido de l0. Si el número de muertes
debidas a esta enfermedad sigue una distribución de Poisson , cual es la probabilidad de que
en el año que transcurre:
a. Mueran exactamente siete (7) personas de esa enfermedad.
c. Mueran l0 o más personas de esa enfermedad.
20. Si los valores de colesterol total para cierta población están distribuidos normalmente
con media 200 mg / ml y una desviación estándar de 20 mg / ml, hallar la probabilidad de
que un individuo escogido al azar tenga un grado de colesterol entre:
a) l80 y 200 miligramos por mililitro.
b) Mayor que 225 miligramos por mililitros.
21. La cantidad semanal que una compañía gasta en mantenimiento y reparaciones sigue
una distribución normal con media $400 y una desviación estándar de $20. Si el
presupuesto para cubrir los gastos de reparación para la semana siguiente es de $450.
a. Cual es la probabilidad que los costos reales sobrepasen la cantidad presupuestada
b. Cuanto debe ser el presupuesto semanal para gastos y reparaciones para que tan solo re
rebase con una probabilidad del 0.1
22. El tiempo por semana que una empresa de contadores usa la unidad central de proceso
(U C P ) tiene como función de densidad de probabilidad ( medido en horas)
(3/64)x2(4 - x)
f(x) =
0
a. Calcular el valor esperado y la varianza del tiempo por semana que se usa la U C P
b. El tiempo que se usa la U C P le cuesta a la empresa $200 por hora. Calcular el valor
esperado y la varianza del costo semanal por usar la U P C.
23. La llegada de clientes a la ventanilla de un banco sigue una distribución de poisson con
promedio de 8 por hora . Para una hora determinada , calcular la probabilidad de:
a. Lleguen exactamente 8 clientes
b. No lleguen mas de 3 clientes
c. Lleguen por lo menos dos clientes
24. Al estudiar las ofertas bajas de contratos de envíos , una empresa fabricante de
computadoras ve que los contratos intraestados tienen ofertas bajas que se distribuyen
uniformemente entre 20 y 25 unidades , en miles de dólares . Calcular la probabilidad que
la oferta baja del siguiente contrato de envío intraestatal sea :
a. Menor que 22000
b. Mayor que 24000
c. Calcular el costo promedio de las ofertas bajas de este tipo
25. Una empresa vende cuatro artículos seleccionados al azar de un lote grande del cual se
sabe que el 10% son defectuosos. Si Y cuenta el numero de defectuosos de los cuatro que
se vendieron:
a. calcule la probabilidad de que a lo mas un articulo de los cuatro sea defectuoso
b. el comprador de las piezas las regresa con un costo de C = 3Y2 + Y + 2 dólares. Calcule
el valor esperado del costo
26. El numero de vehículos que pasa por determinada parte es 10 por minuto en promedio.
Calcular:
a. la probabilidad de que en un minuto cualquiera pasen por lo menos 15
b. la probabilidad de que en intervalo cualquiera de dos minutos pasen por lo menos 15.
27. Suponga que una variable aleatoria X tiene como función de densidad de
probabilidad a:
Cx2 +x
si 0  x  2
f(x)=
0
en oro caso
a. Encuentre el calor de
b. Encuentre F(x) y grafique F y f
c. Calcule P( X  1) , P(0  X 1,5 )
d. Calcule E(X) , V(X)
28. Suponga que las calificaciones de los estudiantes se distribuyen en forma normal con
media 2.0 y varianza 0.5. Si se realiza un examen ¿Qué porcentaje de estudiantes pasaran
el examen si este se aprueba con una nota superior a tres. Y además cual es la probabilidad
de que un estudiante escogido al azar obtenga un anota ente cuatro y cinco
30. En un proceso de sinterización de dos tipos de polvo de cobre se considera la
proporción de volumen de cobre sólido Y y la proporción de cristales X. Si las funciones de
densidad de X e Y están definidas por:
6x(1 x) si 0  x 1
f X (x)  
0, en otocaso
3y2 si 0  y  1
g Y (y)  
0, en otocaso
Hallar la función de distribución de probabilidad para Z = XY , sabiendo que X e Y son
Independientes.
ESTIMACION Y PRUBAS DE HIPOTESIS
31. Suponga que una variable aleatoria X sigue una distribución de poisson de parámetro 
Se dispone de una muestra aleatoria X1, X2, X3, X4,,,,Xn de observaciones . Determine un
estimador de máxima verosimilitud para  apoyado en la muestra.
32. Las mediciones de dureza Rockwell de lingotes de acero se lleva acabo oprimiendo una
punta de diamante en el acero y midiendo su profundidad de penetración . Una muestra de
15 de estas mediciones mostró un promedio de 65 y una varianza de 90 . estimar la dureza
verdadera en un intervalo de confianza de 95%.
33. La resistencia del caucho a la abrasión aumenta si se agrega una carga de sílice y un
agente de acoplamiento para enlazar químicamente a la carga con cadenas de polímeros:
50 muestras de caucho con el agente de acoplamiento tipo Y dieron una resistencia
promedio de 92 y una varianza de 20. 40 muestras de caucho con el agente de acoplamiento
tipo II dieron un promedio de 98 y una varianza de 30 . Estimar la diferencia verdadera
entre las resistencias promedio a la abrasión en un intervalo de confianza de 95%.
34. Al probar 100 resistores que fabrico la compañía A se encontró que 12 no cumplieron
con las especificaciones de tolerancia . Determinar un intervalo de confianza de 95% para
la fracción verdadera de los resistores que tienen averías .
b. Si se quiere que el error en la estimación de la proporción verdadera de los resistores que
no cumplen con las especificaciones sea de 0.05 con un coeficiente de confianza 95% .
Cuantos resitores se deben muestra?
35. En cierta población de alcohólicos, la duración promedio del abuso de alcohol es de l2
años y desviación típica de 6 años. ? Cual es la probabilidad de que en una muestra
aleatoria de 36 individuos tenga una duración promedio de abuso del alcohol entre l0 y 11
años?.
36. Si las concentraciones de ácido urico en los adultos masculinos están distribuidos
aproximadamente en forma normal con medio 5.7 y desviación típica1 encontrar la
probabilidad de que en una muestra de 9 hombre, la media sea:
a) mayor que 6
b) entre 5 y 6.
37. Si, en una población de mujeres el l5% están sometidas a cierta dieta, cual es la
probabilidad de que en una muestra de 100 mujeres se encuentre, que la proporción que se
encuentra a dieta sea:
a) Mayor o igual al 20%
b) No mayor que el l2%..
38. Una compañía opera cuatro maquina en tres turnos diarios. A partir de los registros de
producción, se colectan los siguientes datos respecto al numero de interrupciones.
TURNO
1
2
3
A
41
31
15
MAQUINAS
B
C
D
20
12
16
11
9
14
17
16
10
Determinara si el turno y las maquinas son independientes respecto del numero de
interrupciones a un nivel de confianza del 5%
39. Suponer que X1, X2 , X3,,,,,,,Xn representa una muestra aleatoria de una distribución
norma con promedio  y varianza 2 determinar los estimadores de posibilidad máxima
para  y 2
40. Se implementa una nueva política de retiro por enfermedad en una empresa. Una
muestra de las opiniones de los empleados mostró las siguientes clasificaciones, por sexo y
por opinión.
Hombres
Mujeres
En favor
31
42
En contra
44
36
Indecisos
6
8
¿Esta relacionada la reacción a la nueva política con el sexo? .Probar en el nivel de
significación de 5%
41. El flujo de agua a través del suelo depende de la porosidad del suelo . Para comparar
dos tipos de suelo arenoso , se tomaron dos muestras n1 = 50 mediciones del suelo A y n2=
100 mediciones del suelo B suponer que si 1 = 0.01 y 2 = 0.02 calcular la probabilidad
de que la diferencia entre los promedios muéstrales quede dentro de 0.05 unidad de la
diferencia verdadera 1- 2
42. Suponga que ˆ1 y ˆ2 son dos estimadores insesgados de un parámetro  tal ue
demuestre que ˆ3  aˆ1  (1  a)ˆ2 para 0  a  1 es un
V(1 )  12 y V( 2 )   22
estimador insesgado de  y además si ˆ y ˆ son independientes encontrar un valor de a
1
2
de tal forma que V( ˆ3 ) sea mínima
43. suponga que y1, y2, y3,,,,,,,,,yn, es una muestra aleatoria de mediciones con respecto a
las proporciones de impurezas de unas muestras de mineral de hierro, cada yi tiene una
función de densidad de probabilidad:
3y2
si 0 <x<1
f(y) =
0 en otro caso
Un comprador potencial rechazara el mineral si el promedio muestral es mayor que 0.7 .
¿Cuál es la probabilidad de que el mineral sea rechazado?
44. Para comparar las proporciones de artículos defectuosos producidos por dos líneas de
producción se seleccionaron muestras aleatorias independientes de 100articulos de cada
línea. La línea A produjo 18 defectuosos y la línea B 12. obtenga un intervalo del 98% para
la diferencia de las proporciones de defectuosos para las dos líneas. ¿Existe evidencia
suficiente para sugerir que una línea produce mas defectuosos que la otra?
45. Un experimento con casquillos de artillería produjo los siguientes datos acerca de las
características de las desviaciones laterales y alcances ¿ concluirá usted que las
desviaciones y el alcance son independientes?
DEVIACION LATERAL
ALCANCE (YARDAS)
IZQUIERDA
NORMAL
DERECHA
0 – 2000
2000 - 6000
6000 - 12000
6
9
8
14
11
17
8
4
6
46. Una constructora ha ganado el 60% de los trabajos en los que concursado. Supóngase
que el mes próximo la empresa va a concursaren 25 proyectos .
a. Calcule la probabilidad de que gane por lo menos 20 de ellos
b. Calcule la probabilidad de que el numero de trabajos que gane este entre 10 y 23
47. Un determinado tipo de resistor se vende bajo la especificación de que la varianza de
las resistencias es de alrededor de 50 ohms .Se va a probar una muestra de15 de dichos
resistores midiendo sus resistencias . Calcular de que la varianza S2 de la muestra :
a. Sea mayor de 80
b. Sea menor que 20
c. Determine un intervalo en el que deban queda al menos el 75% de las varianzas de la
muestra
d Que hipótesis son necesarias para que las repuestas sean validas
48. Suponga que se toman 3 muestras aleatorias de 3 poblaciones X1 , X2, X3 de tamaños
n1 ,n2 ,n3 respectivamente . Si cada Xi  N(i , i ) y además son independientes calcule la
distribución de Y = X1 + X2 + X3
49. Un supervisor de producción sospecha que existe diferencia entre la proporciones
p1 y p 2 de artículos defectuosos producidos por maquinas distintas. La experiencia ha
demostrado que la proporción de defectuosos para cada maquina es del orden del 0.3 . Si el
supervisor quiere estimar las diferencia en las proporciones con una exactitud de 0,05 y una
probabilidad del 95% de que sea correcta ¿cuántos artículos debe muestrear aleatoriamente
de cada maquina? (Suponga que los tamaños de muestra de cada población son iguales)
50. El PCDD es un contaminante emitido por incineradores de desechos sólidos, vehículos
de motor, fabricas de acero y producción de metales. Se tomaron muestras de aire en dos
ciudades distintas Bogota (11 días) y Medellín ( 3 días) . los niveles de PCDD ( en gr/m 3)
en cada ciudad se muestran a continuación.
Bogota:
Medellín:
2.38 3.03 1.44 0.47
0.5
0.50 0.22 0.26 0.31
0.61
0.46 1.09 2.14
0.90
utilice la estimación por intervalos para comparar la variación de los niveles de PCDD en
cada ciudad ¿ que hipótesis son necesarias para que el análisis sea valido?
51.A fin de evaluar el impacto del accidente nuclear en una ciudad de Pensilivania en
marzo de 1979, se diseño un cuestionario que se envió por correo a 150 familias del área
inmediatamente después del accidente y en el que se les preguntaba que opinión tenían del
uso de la energía nuclear para generara electricidad para el consumo, naturalmente este
estudio de opinión se tenia antes del accidente. Los datos se muestran a continuación.
Antes del accidente
Después del accidente
En favor
62
52
En contra
35
72
indiferente
53
26
a. establezca un intervalo del 99% para la diferencia de las verdaderas proporciones de los
residentes que estaban a favor de la energía nuclear antes y después del accidente
b. Haga lo mismo que en el punto a pero para los que están en contra.
52. suponga que X1, X2,X3,,,,,,,,,Xn es una muestra aleatoria de una variable aleatoria que se
distribuye Poisson de parámetro  .
a. encuentre un estimador de máxima posibilidad para 
b. encuentre un intervalo de confianza del (1- )% para  ( utilice el teorema del limite
central suponiendo n grande)
53. Se afirma que las mediciones de resistencia a la tensión de una varilla de acero de 12
mm deberían ser en promedio de por lo menos 8 unidades (N/mm2) mayor que las
correspondientes a una varilla de 10 mm. Las muestras independientes de 50 mediciones
cada una para los dos tamaños de varilla dieron los resultados siguientes:
x1  545 x 2  555 S1  24 S2  18
Se justifica la afirmación en un nivel de significancia del 5%
53. Un inspector de control de calidad compara las mediciones de la resistencia máxima a
la tensión para un alambre pretensado clase II y clase III toma una muestra de cinco
especimenes de un rollo de cada clase y los prueba en el ,laboratorio. Los datos de las
muestras en miles de lb/pul2 son los siguientes:
clase I 253 261 258 255 256
clase II 274 275 271 277 276
determine si los promedios son iguales o distintos con un nivel de significancia del 0.01%
54. Las capacitancias de cierto tipo de capacitador están distribuidas normalmente con
promedio 53 micro faradios y una desviación estándar de 2 micro faradios. Si se usan 64
capacitadores en un sistema electrónico calcular la probabilidad aproximada de que por lo
menos 12 de ellos tengan capacitancias menores que 50 micro faradios.
55. Un supervisor de una fabrica esta interesado en presupuestar los costos semanales para
cierto tipo de máquina los estudios anteriores indican que estos costos tienen una
distribución exponencial con media 20 para cada máquina sean y1 ,y2 , ,,,y5 los cotos de
reparación para cinco máquinas para la próxima semana. Determine un número talque:
5
P( y k  c)  0.05
k 1
56. la resistencia a la ruptura de los hilos tiene una desviación estándar de 18 gramos.
¿cuántas mediciones de la resistencia a la ruptura debe hacerse para en el siguiente
experimento si la resistencia promedio de ruptura debe estar a menos de 4gramos de la
resistencia verdadera a la ruptura, con un coeficiente de confianza del 90%?.
57. Suponga que X1, X2, X3,,,,,,,,Xn y Y1, Y2, Y3,,,,,,,,Ym Son dos muestras aleatorias de
dos poblaciones independientes X e Y respectivamente. Si X  N(1,  12 )
Y  N(2,  22 ) entonces:
a. calcule E( X  Y )
b. V( X  Y )
c.  12 = 2 y  22 = 2.5 con m=n determine el tamaño de la muestra tal que ( X  Y ) se
aleje a lo mas en una unidad de 1- 2 con una probabilidad de 95%
58. los tiempos que tarda un cajero en procesar el pedido el pedido de cada persona son
variables aleatorias independientes con media 1.5 minutos y una desviación estándar de 1 ¿
Cual es la probabilidad aproximada de que se puedan procesar los pedidos de 100 personas
en menos de dos horas?
59. Una línea aérea se da cuenta que el 5% de las personas que hacen las reservaciones para
cierto vuelo no se presentan. Si la aerolínea vende 160 boletos para el vuelo con solamente
155 puestos ¿ Cual es la probabilidad de que haya un asiento disponible para cada persona
con reservación que se presenta para el vuelo?
60. Suponga que X1,X2 ,X3,,,,,,, X40 representa una muestra aleatoria de las proporciones de
impurezas en muestras de de mineral de hierro y que dichas proporciones tienen función de
densidad de probabilidad a:
º
3x2
si
0x1
f X (x) 
0
en otro caso
un comprador rechaza el mineral si X  0.7 calcular la probabilidad de que el mineral sea
rechazado, basándose en las 40 muestras
61. El tiempo muerto diario de una instalación de computo es en promedio 4 horas con una
desviación estándar de 0.8 horas.
a. calcular la probabilidad de que el tiempo muerto promedio en un espacio de 30 días este
entre 1 y 5 horas
b. calcular la probabilidad de que el tiempo muerto total en los 30 días sea menor que 115
horas
c. ¿ Qué hipótesis son necesarias para que las respuesta en a y b sean validas
62. Un plan de muestreo para aceptar un lote grande requiere el muestreo de 50 artículos y
aceptar el lote si el número de defectuoso no es mayor de 5 calcular la probabilidad de
aceptar un lote si la proporción de defectuosos del lote:
a) 10% b) 20% c) 30%
63. Suponga que una variable aleatoria X tiene como función de densidad a:
( +1)x si 0  x  1
f(x) =
0 en otro caso
Si X1 , X2 , X3 ,,,,,,,,,,,Xn es una muestra aleatoria de X encuentre un estimador de máxima
verosimilitud para 
64. Si X1 , X2 , X3 ,,,,,,,,,,,Xn es una muestra aleatoria que se distribuye poisón de parámetro
 , encuentre un intervalo de confianza del (1-  )% para  para n grande
65. Se están investigando dos métodos para producir gasolina a partir del petróleo crudo. Se
supone que el rendimiento en ambos procesos se distribuye en forma normal. Los
siguientes datos se han obtenido en una planta piloto.
PROCESO
1
2
RENDIMIENTOS EN %
24,2 26,6 25,5 24,8 25,9 26,5
21,0 22,1 21,8 20,9 22,4 22,0
¿Hay alguna razón para creer que el proceso 1 tiene un rendimiento medio
mayor? Con un nivel de significancía del 5%
66. los siguientes son los tiempos de quemado de señales luminosas de dos tipos diferentes
TIPO I
63 82
81 68
57 59
66 75
82 73
TIPO II
64 56
72 63
83 74
59 82
65 82
a. Pruebe la hipótesis de que las varianzas son iguales a un nivel de significancia del 5%
b. Use a para probar que la hipótesis de que los tiempos medios son iguales
REGRESION
67. la resistencia del papel usado en la mano factura de cajas de cartón (y) se relaciona con
el porcentaje de concentración de madera dura en la pulpa original (x) : en condiciones
controladas, una planta piloto manufactura 16 muestras y se mide la resistencia a la
tensión. La información se muestra en la siguiente tabla.
101,4
117,4
117,1
106,2
131,9
146,9
146,8
133,9
111,3
123,0
125,1
145,2
134,3
144,5
143,7
146,9
2075,6
x
1,0
1,5
1,5
1,5
2,0
2,0
2,2
2,4
2,5
2,5
2,8
2,8
3,0
3,0
3,2
3,3
37,2
Lny
4,62
4,8
4,8
4,7
4,9
5,0
5,0
4,9
4,7
4,8
4,8
5,0
4,9
5,0
5,0
5,0
77,7
Lux
0
0,4
0,4
0,4
0,7
0,7
0,8
0,9
0,9
0,9
1,0
1,0
1,1
1,1
1,2
1,2
12,7
xy
101,4
176,1
175,7
159,3
263,8
293,8
323,0
321,4
278,3
307,5
350,3
406,6
402,9
433,5
459,8
484,8
4938,0
(Lnx)(Lny) (LnX)^2
0
0
1,9
0,2
1,9
0,2
1,9
0,2
3,4
0,5
3,5
0,5
3,9
0,6
4,3
0,8
4,3
0,8
4,4
0,8
5,0
1,1
5,1
1,1
5,4
1,2
5,5
1,2
5,8
1,4
6,0
1,4
62,2
11,8
(Lny)^2
21,3
22,7
22,7
21,8
23,8
24,9
24,9
24,0
22,2
23,2
23,3
24,8
24,0
24,7
24,7
24,9
377,9
x^2
0
0,2
0,2
0,2
0,5
0,5
0,6
0,8
0,8
0,8
1,1
1,1
1,2
1,2
1,4
1,4
11,8
y^2
10282,0
31011,2
30852,9
25376,5
69590,4
86318,4
104303,2
103272,2
77423,1
94556,3
122696,1
165291,0
162328,4
187922,3
211452,8
235002,0
1717678,7
a. Estime los modelos y = 0 + x + ; y =0 ex ; y = =0x, con la información de
la tabla
b. Para cada modelo elabore la tabla de ANOVA
c. Determine cual de los modelos es el mas apropiado para moldear la resistencia,
justificando su respuesta, a través de: ANOVA, coeficiente de determinación, y
pruebas sobre los parámetros de los modelos
68. Supóngase que se ajusta el modelo
y   0  1 x1   2 x2   3 x1 x2   4 x12   5 x22  
n = 30 puntos de datos, y que SEC = 0.37 R2 = 0.89
¿Sugieren estos datos de SEC y R2 que el modelo se ajusta bien a los datos? Explicar la
respuesta
b. ¿ Determine si el modelo predice la respuesta y con un nivel de significancía del 5%
69. una respuesta Y es una función de tres variables independientes x 1 , x2, x3 que se
relacionan mediante el modelo:
Y=  x1+ 2x2+ 2x3 + 0 + 
a. ajuste el modelo a los datos
sugerencia:
Y
1
0
0
1
2
3
3
x1
-3
-2
-1
0
1
2
3
x2
5
0
-3
-4
-3
0
5
X3
-1
1
1
0
-1
-1
1
 14 
28 0 0 0
 10 
 0 84 0 0
t
t


XX =
XY = 
  3
 0 0 6 0
 


 10 
 0 0 0 7
b. construya la tabal de ANOVA
c) pruebe H0: E(Y)  0 + 1 x1+ 2x2+ 2x3 vs Ha: E(Y) = 0 +  x1+ 2x2+ 2x3
d) Pruebe, par cada j=0,1,2,3 H0: j = 0 vs Ha : j  0
e) encuentre un intervalo de confianza del 95% para cada j
70. Una empresa de telefonía esta interesada en estudiar los ingresos anuales Y (en miles de
millones de pesos) contra en precio medio de las llamadas internacionales X en (cientos de
pesos): para tal efecto se tomaron 35 observaciones en donde se obtuvieron los siguientes
resultados
x = 17,22  y = 84,945 SCT = 12,144
R2 = 0.7378 Sxy = -0,134
a. estime el modelo Y = 1x + 0
b. Considera que el precio medio explica los ingresos con un nivel de significancía del
5%
c. Que nivel de ingresos se espera para el próximo año si el precio es de 0.52?