REGRESION LINEAL SIMPLE

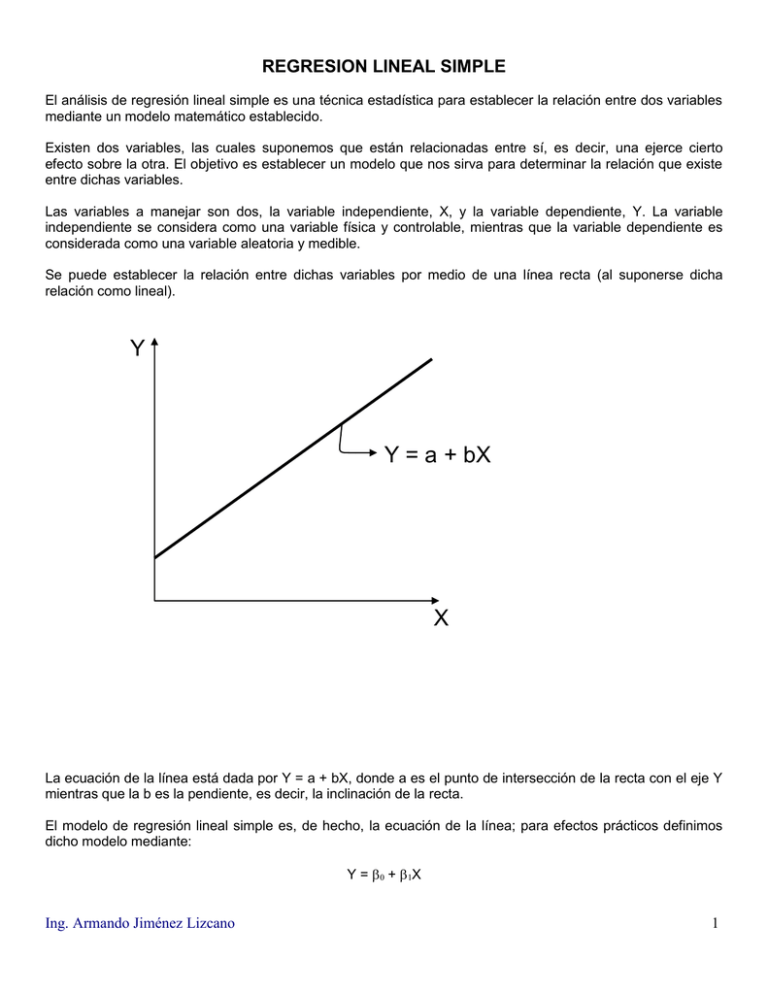
REGRESION LINEAL SIMPLE
El análisis de regresión lineal simple es una técnica estadística para establecer la relación entre dos variables
mediante un modelo matemático establecido.
Existen dos variables, las cuales suponemos que están relacionadas entre sí, es decir, una ejerce cierto
efecto sobre la otra. El objetivo es establecer un modelo que nos sirva para determinar la relación que existe
entre dichas variables.
Las variables a manejar son dos, la variable independiente, X, y la variable dependiente, Y. La variable
independiente se considera como una variable física y controlable, mientras que la variable dependiente es
considerada como una variable aleatoria y medible.
Se puede establecer la relación entre dichas variables por medio de una línea recta (al suponerse dicha
relación como lineal).
Y
Y = a + bX
X
La ecuación de la línea está dada por Y = a + bX, donde a es el punto de intersección de la recta con el eje Y
mientras que la b es la pendiente, es decir, la inclinación de la recta.
El modelo de regresión lineal simple es, de hecho, la ecuación de la línea; para efectos prácticos definimos
dicho modelo mediante:
Y =  + X
Ing. Armando Jiménez Lizcano
1
Donde 0 y 1 son los parámetros del modelo.
0 representa la ordenada en el origen, esto es, el punto donde la recta corta el eje Y.
1 representa la pendiente, esto es, el cambio esperado en Y por cada incremento unitario en X.
ESTIMACION DE PARAMETROS
El modelo anteriormente descrito representa la
X y Y. Es necesario encontrar los valores de 0
parámetros.
Para encontrar estos estimadores, partiremos
valores de X y de Y:
X1
X2
X3
.
.
.
Xn
Y1
Y2
Y3
.
.
.
Yn
relación real existente entre las dos variables,
y 1 que nos sirvan para estimar dichos
de una muestra aleatoria de tamaño n para
Al ser una muestra aleatoria, el error estará presente en dichas mediciones. Debemos considerar dicho error
en el modelo de regresión a fin de representar, mediante éste, cada una de las observaciones anteriores:
Y = 0 + 1X + 
Donde  es un error aleatorio con media cero y varianza 2.
Al utilizar el modelo anterior para representar cada observación de Y, éstas quedarán de la siguiente manera:
Ing. Armando Jiménez Lizcano
2
Y1 = 0 + 1X1 + 1
Y
Y2 = 0 + 1X2 + 2
Y3 = 0 + 1X3 + 3
.
.
.
.
.
.
.
.
.
Y = 0 + 1X
.
.
.
Y = 0 + 1X + 
Yn = 0 + 1Xn + n
X
En general, Yi = 0 + 1Xi + i para i = 1, 2, 3, ..., n
METODO DE MINIMOS CUADRADOS
Para encontrar los estimadores de los parámetros, utilizaremos el método de mínimos cuadrados.
El método de mínimos cuadrados consiste en minimizar la función de mínimos cuadrados.
La función de mínimos cuadrados está dada por:
n
L    i2
i 1
Si de Yi = 0 + 1Xi + i despejamos i y sustituimos dicha expresión en L:
n
n
i 1
i 1
L    i2   Yi   0  1 X i 
2
Buscaremos aquellos valores de  0 y  1 que minimicen la ecuación anterior. Para esto, derivaremos la función
y evaluaremos con respecto a ̂ 0 y ̂1 ( los estimadores) e igualaremos a cero.
Ing. Armando Jiménez Lizcano
3
L
 0
0
ˆ 0 ,ˆ1
L
1
0
ˆ 0 ,ˆ1
Dichas derivadas resultan en:
L
 0
L
1
n
ˆ 0 , ˆ1
 2 Yi  ˆ 0  ˆ1 X i   0
i 1
n
ˆ 0 , ˆ1
 2 Yi  ˆ 0  ˆ1 X i X i  0
i 1
Lo cual nos lleva a las siguientes ecuaciones conocidas como ecuaciones normales de mínimos
cuadrados.
n
n
i 1
i 1
 Yi  nˆ 0  ˆ1  X i  0
n
n
n
i 1
i 1
i 1
 X iYi  ˆ 0  X i  ˆ1  X i2  0
Despejando ˆ 0 y ˆ1 :
 0  Y  1 X
n
n
1 
Ing. Armando Jiménez Lizcano
X Y
i 1
i i

n
 X i  Yi
i 1
i 1
n
 n

 Xi 
n
X i2   i 1 

n
i 1
2
4
Si definimos las siguientes expresiones:
Sxx, como la suma corregida de los cuadrados de X:
n
Sxx    X i  X 
2
i 1
 n

X



i
n
i 1


2
  Xi 
n
i 1
2
y Sxy, como la suma corregida de los productos cruzados de X y de Y:
n
n
n
n
 X Y
i 1
i 1
n
Sxx   Yi  X i  X    X i Yi 
i 1
i
i 1
i
,
entonces ̂1 se puede expresar también como:
̂1 
Sxy
Sxx
Por lo tanto, el modelo de regresión lineal simple ajustado queda de la siguiente forma:
Yˆ  ˆ 0  ˆ1 X
donde ˆ 0 y ˆ1 son los estimadores de los valores verdaderos de la ordenada en el origen y la pendiente,
respectivamente.
INFERENCIA EN LA REGRESION LINEAL SIMPLE
Podemos generalizar sobre los parámetros del modelo a partir de la información obtenida de los estimadores
de éstos. Dicha generalización ( o inferencia estadística) se puede realizar ya sea mediante pruebas de
hipótesis o mediante intervalos de confianza.
PRUEBAS DE HIPOTESIS EN LA REGRESION LINEAL SIMPLE
PARA LA ORDENADA EN EL ORIGEN
Deseamos probar la hipótesis de que 0 es igual a un valor determinado contra la alternativa apropiada,
digamos por ejemplo, diferente a dicho valor; esto es:
H 0 :  0   0,0
H a :  0   0,0
El estadístico de prueba apropiado será:
Ing. Armando Jiménez Lizcano
5
t0 
ˆ 0   0,0
1 X 2 
MSE 

 n Sxx
donde:
MSE es la media de los cuadrados del error o bien, el estimador de la varianza del modelo:
 2  MSE 
SSE
n2
en este caso SSE es la suma de los cuadrados del error y n – 2 son los grados de libertad del error.
SSE  Syy  SSR
Syy es la suma corregida de los cuadrados de Y o la suma total de cuadrados:
 n 
  Yi 
n
2
Syy   Yi   i 1 
n
i 1
2
y SSR es la suma de cuadrados de la regresión:
SSR  ̂1 Sxy
Retomando la hipótesis planteada:
H 0 :  0   0,0
H a :  0   0,0
t0 
ˆ 0   0,0
1 X 2 
MSE 

 n Sxx
este estadístico sigue una distribución t-student con v = n – 2 grados de libertad.
En el estadístico de prueba vemos que
1 X 2 
MSE 
 representa la desviación estándar para 0.
 n Sxx
Si el valor absoluto del estadístico de prueba es mayor que el valor de tablas, t /2, n – 2, entonces rechazaremos
la hipótesis nula; aceptaremos la alternativa concluyendo que la ordenada en el origen es diferente al valor
con el cual la estamos comparando.
Ing. Armando Jiménez Lizcano
6
PARA LA PENDIENTE
Algo semejante realizaremos para la pendiente. Partimos de la hipótesis nula afirmando que la pendiente es
igual a un valor determinado (siempre que dicho valor sea diferente de cero), contra la alternativa apropiada,
por ejemplo que sea diferente a dicho valor:
H 0 :  1   1,0
H a :  1   1,0
el estadístico de prueba en este caso es:
t0 
ˆ 1  1,0
MSE
Sxx
Este estadístico también sigue una distribución t-student con v = n – 2 grados de libertad.
Del mismo modo, la expresión
MSE
representa la desviación estándar para 1.
Sxx
Si el valor absoluto del estadístico de prueba es mayor que el valor de tablas, t/2, n – 2, entonces se rechaza la
hipótesis nula y se acepta la alternativa: la pendiente es diferente al valor representado por 1,0.
Un caso especial para la pendiente sería probar la hipótesis nula afirmando que la pendiente es igual a cero
contra la alternativa que sea diferente de cero.
También conocido como Prueba de Significancia, nos ayuda a determinar si la variable independiente tiene o
no efecto significativo sobre la variable dependiente.
Para realizar este procedimiento de prueba de hipótesis, descomponemos la suma total de cuadrados en dos
partes: la suma de cuadrados de la regresión y la suma de los cuadrados del error.
Syy  SSR  SSE
Entonces:
H 0 : 1  0
H a : 1  0
Ing. Armando Jiménez Lizcano
7
También hacemos uso de la tabla de análisis de varianza (ANOVA) para determinar el estadístico de prueba.
Dicha tabla se compone de lo siguiente:
Fuente de
variación
Suma de
cuadrados
Grados de
libertad
Regresión
SSR
1
Error
SS
n-2
Total
Syy
n-1
Media de
cuadrados
SSR
1
SSE
MSE 
n2
MSR 
Estadístico de
prueba
F0 
MSR
MSE
Este estadístico de prueba sigue una distribución F (Fisher)con v1 = 1 y v2 = n – 2 grados de libertad en el
numerador y en el denominador, respectivamente.
En este caso si el estadístico de prueba es superior que el valor de tablas (de la distribución F), Fn – 2, se
rechaza la hipótesis nula y por consiguiente se acepta la alternativa, concluyendo que la variable
independiente (X) si tiene efecto significativo sobre la variable dependiente (Y).
En las pruebas descritas anteriormente el valor de representa el nivel de significancia en la prueba de
hipótesis, esto es, la probabilidad de rechazar la hipótesis nula.
INTERVALOS DE CONFIANZA EN LA REGRESION LINEAL SIMPLE.
Como vimos anteriormente, a parte de las pruebas de hipótesis; también podemos generalizar sobre los
parámetros a partir de los estimadores, mediante intervalos de confianza. Esto es, encontraremos dos límites,
inferior y superior, dentro de los cuales se encontrará el valor verdadero del parámetro del modelo en
cuestión.
Así, para la ordenada en el origen, el intervalo de confianza de (1 - ) 100%, para este parámetro está dado
por la siguiente ecuación.
ˆ 0  t
2
,n  2
1 X 2 
1 X 2 
MSE 
   0  ˆ 0  t ,n2 MSE 

2
 n Sxx
 n Sxx
Aquí, como 0 representa solamente una posición, no debe existir problema alguno en cuanto a la conclusión
de los resultados obtenidos.
Ing. Armando Jiménez Lizcano
8
Igualmente, también podemos calcular un intervalo de confianza de (1 - ) 100%, para la pendiente verdadera
del modelo mediante la siguiente expresión.
ˆ 1  t
2
,n  2
MSE
MSE
 1  ˆ 1  t ,n2
2
Sxx
Sxx
En este caso la conclusión si depende del resultado obtenido, veamos los casos posibles:
Puede que el intervalo resulte en  a  1  b ; la conclusión apropiada será que por cada incremento en X,
Y, disminuirá, en promedio, por lo menos b y a lo mucho a veces.
Otro resultado posible para el intervalo sería a  1  b ; la conclusión será, en este caso, que por cada
incremento en X, Y se incrementará, en promedio, por lo menos a y a lo mucho b veces.
Si el resultado del intervalo es  a  1  b , en este caso, solamente concluiremos que no se puede afirmar
que X tenga efecto sobre Y.
INTERVALOS DE CONFIANZA PARA LA RESPUESTA MEDIA Y PARA UNA PREDICCION
FUTURA
El modelo de regresión lineal simple ajustado Y  ˆ 0  ˆ1 X nos permite establecer como es la relación entre
X y Y, de que medida X afecta a Y. También podemos utilizar este modelo para predecir un valor futuro de Y
dado un valor determinado de X.
Esto es, ¿Cuál es el valor esperado de Y cuando X = X0?, solamente hay que introducir el valor de X0 en la
variable X del modelo.
Yˆ  ˆ 0  ˆ1  X 0 
Podemos calcular intervalos de confianza tanto para la media de una serie de observaciones (para la recta
verdadera) como para una observación futura en particular.
El intervalo de confianza de (1 -100% para el valor esperado de Y cuando X = X0, esta dado por la
ecuación:
Ing. Armando Jiménez Lizcano
9
Yˆ0  t
2
,n  2
 1 X 0  X 2 
 1 X 0  X 2 
MSE 
   y  Yˆ0  t ,n2 MSE 

2
Sxx 
Sxx 
 n
 n
El intervalo de confianza de (1 - ) 100% para una observación futura de Y cuando X = X0, está dado por la
expresión:
ˆ 0  t
Y
2
,n 2
 1 X 0  X2 
 1 X 0  X2 
ˆ
MSE 1  
  Y0  Y0  t  ,n2 MSE 1  

2
Sxx 
Sxx 
 n
 n
Si deseamos determinar un intervalo de confianza de (1 - ) 100% para k observaciones futuras haremos:
Yˆ0  t
2
,n  2
 1 1 X 0  X 2 
 1 1 X 0  X 2 
MSE  
  Y0  Yˆ0  t ,n2 MSE 

2
Sxx 
Sxx 
 k n
 k n
MEDIDAS DE ADECUACION DEL MODELO
El siguiente paso ahora es determinar si el modelo calculado nos sirve para representar la relación entre las
variables.
Para esto, el modelo tiene que pasar una serie de pruebas ó medidas de adecuación. Dichas medidas son:
El análisis de los residuos
El coeficiente de determinación y
La prueba de falta de ajuste.
ANALISIS DE LOS RESIDUOS
Este procedimiento se emplea para determinar o analizar el comportamiento de la variación de los residuos o
los errores.
Mediante el modelo de regresión lineal simple, calculado a partir de n observaciones en X y Y, podemos
predecir valores estimados de Y para valores determinados de X.
La diferencia entre los valores observados de Y y los valores estimados de esta variable resulta en los errores
o residuos:
Ing. Armando Jiménez Lizcano
10
ei  Yi  Yˆi
Graficamos estos residuos ya sea contra los valores de X, contra los valores estimados de Y, contra los
valores observados de Y o contra la variable tiempo, si es que se tiene.
Basta comparar, esta gráfica con los siguientes patrones para llegar a una conclusión acerca de la adecuación
del modelo:
ei
ei
0
0
Yi
Yi
En este caso, la variación de los
residuos es constante.
El modelo lineal sí es adecuado
La variación crece a medida que la
variable Yi o el tiempo crece.
El modelo no es adecuado.
ei
ei
0
0
Y
La variación es irregular.
El modelo no es adecuado
i
Y
La variación de los residuos no es lineal.
El modelo lineal no es adecuado para expresar
la
i
relación entre X y Y.
Se puede ajustar dicha relación como un modelo
cuadrático, sólo basta agregar una variable de
orden superior.
Y = 0 + 1X + 2X2
COEFICIENTE DE DETERMINACION
Ing. Armando Jiménez Lizcano
11
El coeficiente de determinación nos permite evaluar qué tanta variación de los valores de Y se explica
mediante el modelo de regresión lineal simple.
Este coeficiente de determinación se representa por el símbolo R2; toma valores entre 0 y 1. A medida que se
acerca a 1 el modelo sí es adecuado puesto que explica la mayor cantidad de variación presente en los datos.
En tanto R2 se acerque a cero, el modelo deja de ser adecuado puesto que la cantidad de variación de los
datos que se explica mediante el modelo es pobre.
El coeficiente de determinación se expresa como un porcentaje y se calcula mediante:
R2 
SSR
 100%
Syy
PRUEBA DE FALTA DE AJUSTE
Esta prueba nos permite determinar si el modelo lineal se puede utilizar para representar la relación entre las
variables, principalmente en aquellos casos en los cuales para un mismo valor de X se tienen mas de una
observación en Y:
X1
X2
X3
.
.
.
Xm
Y11
Y21
Y31
.
.
.
Ym1
Y12
Y22
Y32
.
.
.
Ym2
Y13
Y23
Y33
.
.
.
Ym3
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Y1n1
Y2n2
Y3n3
.
.
.
Ymnm
En general se tienen m niveles distintos de X.
En esta prueba partimos de la hipótesis nula:
H0 : El modelo se ajusta a los datos
Contra la alternativa:
Ha : El modelo no se ajusta a los datos
Para este procedimiento se requiere descomponer la suma de cuadrados del error en dos partes:
SSE = SSLOF + SSPE
Donde:
SSLOF es la suma de cuadrados debida a la falta de ajuste.
SSPE es la suma de cuadrados debida al “error puro”
Sabemos que:
Ing. Armando Jiménez Lizcano
12
SSE = Syy - SSR
Entonces:
m
SSPE  
i 1
 Y
ni
i 1
ij
2
 Yi 
Y
SSLOF  SSE  SSPE
El estadístico de prueba apropiado en esta prueba de hipótesis es:
SSLOF
F02 
SSPE
m2
nm
El cual sigue una distribución F con v1  m  2 y v2  n  m grados de libertad en el numerador y en el
denominador, respectivamente.
Si el estadístico de prueba es mayor que el valor de tablas F, m – 2, n – m se rechaza la hipótesis nula y por
consiguiente se acepta la alternativa , el modelo no se ajusta a los datos, por lo tanto, el modelo lineal no es
adecuado para relacionar X y Y.
CORRELACION
Hasta este momento hemos relacionado dos variables que suponemos de antemano tienen una relación entre
sí, esto es, cualquier cambio que provoquemos en la variable independiente, trae como consecuencia un
cambio en la variable dependiente.
Ahora bien, puede haber casos en que las dos variables, X y Y, sean aleatorias; ninguna tiene efecto sobre la
otra, pero sería apropiado relacionar dichas variables (siempre que sea posible).
Podemos relacionar dichas variables mediante el modelo de regresión lineal simple
Y   0  1 X
Aunque éste no nos dice nada sobre la existencia de la relación entre las dos variables.
Es el coeficiente de correlación el que va a determinar si las dos variables están relacionadas entre sí.
El coeficiente de correlación se representa mediante el símbolo  (rho). Se define mediante:

Ing. Armando Jiménez Lizcano
 xy
 x y
13
2
donde  xy
es la covarianza entre X y Y.
El coeficiente de correlación también se puede definir mediante
  1
x
y
Aquí vemos que el coeficiente de correlación está relacionado con 1 sin que esto represente que se trate de
conceptos iguales.
Y
Y
1 > 0
>0
Y
1 < 0
<0
1 = 0
=0
X
X
X
Los estimadores de los parámetros del modelo de regresión son los mismos calculados en temas anteriores:
ˆ 0  Y  ˆ 1 X
ˆ 1 
Sxy
Sxx
En tanto que el estimador del coeficiente de correlación se puede calcular mediante:
r
Sxy
Sxx Syy12
Ahora bien, si elevamos al cuadrado ambos lados de la igualdad:
Ing. Armando Jiménez Lizcano
14
Como
r2 
2
S XY
Sxx  Syy
r2 
Sxy  Sxy
Sxx  Syy
Sxy
 ̂ 1 :
Sxx
r2 
y
̂1 Sxy
Syy
̂1 Sxy  SSR :
entonces:
r2 
SSR
 R2
Syy
Concluimos que el coeficiente de correlación es igual a la raíz cuadrada del coeficiente de determinación
r
SSR
 R2
Syy
Vemos también que el coeficiente de correlación está relacionado con el coeficiente de determinación, aunque
son conceptos totalmente diferentes.
INFERENCIAS SOBRE EL COEFICIENTE DE CORRELACION
Al igual con los parámetros del modelo de regresión, también se pueden hacer inferencias sobre el coeficiente
de correlación verdadero; ya sea mediante pruebas de hipótesis o mediante intervalos de confianza.
PRUEBAS DE HIPOTESIS SOBRE EL COEFICIENTE DE CORRELACION
Para establecer si existe una relación verdadera entre X y Y, podemos realizar la siguiente prueba de
hipótesis:
H0 :   0
Ha :   0
Ing. Armando Jiménez Lizcano
15
Esta prueba es semejante a la prueba de significancia realizada en la regresión lineal simple, aunque tiene
una diferente connotación.
El estadístico de prueba apropiado en este caso es:
t0 
r n2
1 r 2
el cual sigue una distribución t-student con v = n – 2 grados de libertad.
Si el estadístico de prueba es mayor que el valor de tablas t/2,n – 2, se rechaza H0 y por consiguiente se acepta
la alternativa: el coeficiente de correlación es diferente de cero, por lo tanto, las variables sí están
relacionadas entre sí.
También se puede demostrar que el coeficiente de correlación verdadero es igual o diferente a cierto valor
determinado.
Partimos de la hipótesis nula
H 0 :   0
contra la alternativa
H a :   0
El estadístico de prueba es:


zo  tanh1 r   tanh1 0  n  3
donde
tanh 1 x  
1 1 x
In
2 1 x
Este estadístico de prueba sigue una distribución normal estándar.
Entonces, si el valor absoluto del estadístico de prueba es mayor que el valor de tablas z/2, se rechaza H0 y
se acepta la alternativa: el coeficiente de correlación verdadero es diferente del valor con el que se está
comparando.
INTERVALO DE CONFIANZA PARA EL COEFICIENTE DE CORRELACION
Podemos también establecer dos límites, inferior y superior, dentro de los cuales estará el coeficiente de
correlación verdadero.
El intervalo de confianza de (1 – )100% para el coeficiente de correlación está dado por:
Ing. Armando Jiménez Lizcano
16
z 
z



2
    tanh tanh 1 r    2 
tanh tanh 1 r  


n3 
n3 




donde
tanhx  
e x  ex
e x  e x
EJERCICIO
Para ejemplificar lo visto anteriormente, resolveremos el siguiente ejercicio utilizando las fórmula encontradas.
La resistencia del papel utilizado en la manufactura de cajas de cartón ( Y ) se relaciona con el porcentaje
de la concentración de madera dura en la pulpa original ( X ). En condiciones controladas, una planta
piloto manufactura 16 muestras, cada una de diferentes lotes de pulpa, y se mide la resistencia a la
tensión. Los datos son los siguientes.
Ing. Armando Jiménez Lizcano
X
Y
1.0
101.4
1.5
117.4
1.5
117.1
1.5
106.2
17
I.
II.
III.
IV.
V.
VI.
Ajuste un modelo de regresión lineal simple a los datos.
Pruebe la significancia y la falta de ajuste de la regresión. Utilice  = 5 %
Construya un intervalo de confianza del 90 % en la pendiente.
Construya un intervalo de confianza del 98 % en la intersección.
Construya un intervalo de confianza del 95 % sobre la línea de regresión real en X = 2.5
¿Qué porcentaje de la variabilidad en la resistencia del papel se explica a partir de la
concentración de madera dura en la pulpa original?
Ing. Armando Jiménez Lizcano
18
Para encontrar las respuestas a cada uno de los incisos del ejercicio anterior, necesitamos primero calcular
las sumatorias de las variables X y Y:
n=
X =
X2 =
Y =
Y2 =
XY =
16
37.2
93.66
2075.6
272908.02
4937.97
Con los valores anteriores, calcularemos las expresiones Sxx, Sxy que nos permitirán determinar los
estimadores de los parámetros del modelo solicitado en el inciso 1 del ejercicio.
Sxy   XY 
 X  Y 
n
37.2  2075.6
Sxy  4937.97 
16
Sxy  112.2
 X 

2
Sxx   X
2
n
2

37.2
Sxx  93.66 
16
Sxx  7.17
Calculamos enseguida ̂1 a partir de las expresiones anteriores:
Sxy
Sxx
112.2
ˆ 1 
7.17
ˆ 1  15.6485
ˆ 1 
y el valor de ̂ 0 lo calcularemos mediante:
ˆ 0  Y  1 X
ˆ 0  129.725 15.64852.325
ˆ 0  93.3422
Ing. Armando Jiménez Lizcano
19
El primer inciso nos pide ajustar un modelo de regresión lineal simple a los datos:
Yˆ  93.3422  15.6485 X
De aquí concluimos lo siguiente:

La línea de regresión cortará el eje Y en y = 93.3422.

Por cada incremento en la concentración de madera dura en la pulpa original, la resistencia del papel
se incrementará 15.6485 veces en promedio.
Enseguida calcularemos los valores de Syy, SSR y SSE que nos permitirán realizar la prueba de significancia
del modelo.
 Y 
Syy   Y 
n
2
2
Syy  272908.02 
2075.62
16
Syy  3650.81
SSR  ˆ 1 Sxy
SSR  15.6485112.2
SSR  1755.7617
SSE  Syy  SSR
SSE  3650.81  1755.7617
SSE  1895.0483
Para la significancia del modelo planteamos las siguientes hipótesis:
H 0  1  0
H a  1  0
F0 
F0
SSR1 
SSEn  2
1755.7617 

1

1895
.
0483


14
1755.7617
135.3605
F0  12.9710
F0 
Ing. Armando Jiménez Lizcano
20
El valor de las tablas de la distribución F con un nivel de significancia del 5 % con 1 y 14 grados de libertad en
el numerador y el denominador, respectivamente, es 4.6
Al comparar el estadístico de prueba con dicho valor vemos que 12.9710 es mayor que 4.6. esto no lleva a
rechazar la hipótesis nula y por consiguiente a aceptar la alternativa:
La resistencia del papel sí está relacionada significativamente con la concentración de madera dura en
la pulpa original.
En la segunda parte del inciso 2 se pide probar también la falta de ajuste del modelo. Para esto
acomodaremos los valores de X, que estén repetidos en los datos, con sus respectivos valores de Y de la
siguiente forma:
X
1.5
117.4
117.1
2.0
2.5
2.8
3.0
131.9
111.3
125.1
134.3
146.9
123.0
145.2
144.5
 Y
Y
Y
106.2
113.5666
139.4
117.15
135.15
139.4
i
Y
=
2
(117.4 – 113.5666 )2+(117.1 – 13.5666)2+
(106.2 – 113.5666)2 =
(131.9 – 139.4 )2+(146.9 – 139.4)2=
(111.3 – 117.15 )2+(123.0 – 117.5)2=
(125.1 – 135.15 )2+(145.2 – 135.15)2=
(134.3 – 139.4 )2+(144.3 – 139.4)2=
81.4466
112.5
68.445
202.005
52.02
SSpe = 516.4166
La suma de los cuadrados del error es 1895.0483.
La suma de los cuadrados debida al error puro es 516.4166
Y la suma de los cuadrados debida a la falta de ajuste es 1895.0483 – 516.4166 = 1378.6317
En este caso tenemos n = 16 parejas de valores de X y de Y, y m = 10 valores distintos de X.
Planteamos las hipótesis:
H 0 : el modelo lineal se ajusta a los datos
H a : el modelo lineal no se ajusta a los datos
el estadístico de prueba es:
SSlof
F02 
SS pe
m2
nm
1378.6317
8
F02 
516.4166
6
F02  2.0022
El valor de las tablas de la distribución F con un nivel de significancia del 5 % y con 8 y 6 grados de libertad en
el numerador y el denominador, respectivamente, es 4.15
Ing. Armando Jiménez Lizcano
21
Comparando el estadístico de prueba con el valor encontrado en las tablas de la distribución F, vemos que
dicho estadístico es menor que 4.15, por lo tanto no podemos rechazar la hipótesis nula:
No se puede afirmar que el modelo lineal no se ajuste a los datos, por lo que podemos decir que dicho
modelo sí es adecuado para representar la relación entre las variables del ejercicio.
En el inciso 3 se pide calcular un intervalo de confianza del 90% para la pendiente de la línea de regresión.
Para esto necesitamos buscar en las tablas de la distribución t-student el valor de t0.5,14. Este valor en la tablas
es 1.761, por lo que el intervalo de confianza quedará de la siguiente manera:
ˆ 1  t
2
15.6485 1.761
,n  2
MSE
MSE
 1  ˆ 1  t ,n2
2
Sxx
Sxx
135.3605
135.3605
 1  15.6485 1.761
7.17
7.17
7.9970  1  23.2999
aquí concluiremos:
Se puede afirmar con un 90% de certeza que por cada incremento en la concentración de madera dura
en la pulpa original del papel, la resistencia del mismo se incrementará por lo menos 7.9970 y a lo
mucho 23.2999 veces en promedio.
En el inciso 4 se pide un intervalo de confianza del 98 % para la intersección de la recta. Buscaremos en este
caso el valor de t0.01,14 también en las tablas de la distribución t-student. Dicho valor es 2.624, el cual
utilizaremos para calcular el intervalo solicitado:
ˆ 0  t
2
,n  2
1 X 2 
1 X 2 
MSE 
   0  ˆ 0  t ,n 2 MSE 

2
 n Sxx
 n Sxx
 1 2.3252 
 1 2.3252 
93.3422 2.624 135.3605 



93
.
3422

2
.
624
135
.
3605

 

0
7.17 
7.17 
16
16
65.7575  0  120.9268
La conclusión será:
Se puede afirmar con un 98% de certeza que la línea de regresión cortará el eje Y en por lo menos
65.7575 y a lo mucho 120.9268.
Ing. Armando Jiménez Lizcano
22
Para el inciso 5 en el que se pide un intervalo de confianza del 95% para la línea de regresión verdadera en
X = 2.5, buscaremos el valor de t0.025,14 en las tablas de la distribución t-student. Este valor es 2.145.
También necesitamos determinar el valor estimado de Y cuando X es igual a 2.5; para esto introducimos dicho
valor en el modelo de regresión lineal calculado en el primer inciso:
Yˆ0  93.3422 15.6485X 0
Yˆ0  93.3422 15.64852.5
Yˆ0  132.4634
El intervalo de confianza para la respuesta media de Y queda determinado de la siguiente manera:
Y0  t
2
,n  2
 1  X  X 2 
 1  X 0  X 2 
MSE  0



Y

t
MSE

 

Y
0
 ,n  2
2
Sxx 
Sxx 
 n
 n
 1 2.5  2.3252 
 1 2.5  2.3252 
132.4634 2.145 135.3605 



132
.
4634

2
.
145
135
.
3605

 

Y
16
7
.
17
7.17


16

126.0150   Y  138.9123
en este caso concluiremos:
Existe un 95% de certeza al afirmar que cuando la concentración de madera dura en la pulpa original
del papel sea de 2.5%, su resistencia esperada será por lo menos 126.0150 y a lo mucho 138.9123.
Por último, el inciso 6 se pide determinar el porcentaje de la variabilidad en la resistencia del papel que se
explica mediante el modelo de regresión lineal simple. Esto es, calcular el coeficiente de determinación:
SSR
Syy
1755.7617
R2 
3650.81
2
R  0.4809
R2 
esto nos indica que:
El 48.09% de la variabilidad de la resistencia del papel se explica mediante el modelo de regresión
lineal simple:
Yˆ  93.3422  15.6485 X
como el valor de R2 es bajo, podemos concluir que el modelo no es adecuado para representar la relación
entre los valores de X y Y.
Podemos verificar la mayoría de los resultados obtenidos anteriormente en la siguiente hoja de cálculo
diseñada en Excel. Esta hoja arroja automáticamente los valores requeridos para resolver un problema de
regresión lineal simple.
Ing. Armando Jiménez Lizcano
23
X
1
1.5
1.5
1.5
2
2
2.2
2.4
2.5
2.5
Y
101.4
117.4
117.1
106.2
131.9
146.9
146.8
133.9
111.3
123
2.8
2.8
3
3
3.2
3.3
125.1
145.2
134.3
144.5
143.7
146.9
PARAMETROS
0
93.34215481
1
15.64853556

Yo
132.4634937
ESTADISTICOS DE PRUEBA
Fo
12.97105273
to1
8.879216556
to2
3.601534774
INTERVALOS DE CONFIANZA
65.75235768
< o <
120.9319519
7.995711933
< 1 <
23.3013592
126.0154945
< Yo <
138.9114929
106.6904439
< Yo <
158.2365436
COEFICIENTE DE DETERMINACION
X1 :
I.C. para o:
I.C. para 1:
I.C. para
Yo:
I.C. para Yo:
I.C. para :
2.5
0.98
0.9
0.95
0.95
0.95
R^2
0.48092497
COEFICIENTE DE CORRELACION
r
0.693487541
ESTADISTICO DE PRUEBA
to
3.601534774
INTERVALO DE CONFIANZA
0.301389825
Ing. Armando Jiménez Lizcano
<<
0.884970481
24