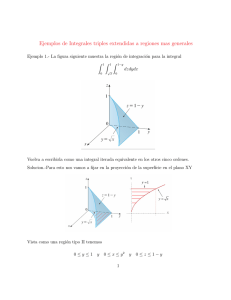
Integrales dobles extendidas a regiones mas generales

Integrales dobles extendidas a regiones mas generales
Sea S una región acotada, e incluyamos S en un rectangulo Q
Sea f una función definida y acotada en S.
Definamos una nueva función f en Q

 f (x, y) si
(x, y) ∈ S
f (x, y) =

0
si (x, y) ∈ Q − S
¿Es integrable f en Q?
Si lo es, decimos que f es integrable en S y que
por
Z Z
Z Z definición
f=
f
Q
S
Consideramos S definido ası́ (Tipo I)

 f (x, y) si
(x, y) ∈ S
Dem. Sea Q = [a, b]x[c.d] un rectángulo que contiene a S y sea f (x, y) =

0
si (x, y) ∈ Q − S
los únicos puntos donde hay discontinuidad para f son los de la frontera de S, puesto que f r(S)
tiene contenido
Z dnulo, f es integrable en Q.
Para x fijo ∃
f (x, y)dy aplicando integración iterada
Z Z
Z b Zc d
f (x, y)dydx si ϕ1 (x) ≤ y ≤ ϕ2 (x) f (x, y) = f (x, y)
f=
Q
a
c
y para todos los demas valores de y en [c, d] f (x, y) = 0
1
S = {(x, y) ∈ R2 |a ≤ x ≤ b y ϕ1 (x) ≤ y ≤
ϕ2 (x)} en donde ϕ1 , ϕ2 son funciones continuas
en [a, b] que cumplen ϕ1 ≤ ϕ2
Teorema: Sea S una región del Tipo I,
comprendida entre las grfáficas de ϕ1 y ϕ2 .
Supongamos que f esta definita y es acotada
en S y que es continua en el interior de S.
RR
Entonces existe la integral doble
f y puede
S
calcularse mediante integración reiterada.
#
Z Z
Z b "Z ϕ2 (x)
f (x, y)dxdy =
f (x, y)dydx
S
Z
d
Z
ϕ2 (x)
f (x, y)dy =
∴
c
Z bZ
Z Z
f (x, y)dy
ϕ1 (x)
ϕ2 (x)
f=
∴
Q
ϕ1 (x)
a
f (x, y)dydx
a
ϕ1 (x)
Analogamente, si consideramos una región T = {(x, y)|c ≤ y ≤ d y ϕZ
1 (y)
Z ≤ x ≤ ϕ2 (y)}
con ϕ1 y ϕ2 funciones continuas en [c, d] siendo ϕ1 ≤ ϕ2 tenemos que
f (x, y)dxdy =
T
Z d Z ϕ2 (y)
f (x, y)dxdy
c
ϕ1 (y)
Ejemplo: Dibujar la región de integración y calcular la integral doble, luego intercambiar el
orden de integración.
Z Z
f (x, y)dA donde f (x, y) = ex+y
y
R = {(x, y) ∈ R2 ||x| + |y| ≤ 1}
R
tenemos que trabajar R por casos para identificar la región de integración
Tenemos entonces que
x > 0,
x < 0,
y > 0 ⇒ |x| + |y| ≤ 1 ⇒ x + y ≤ 1
y > 0 ⇒ |x| + |y| ≤ 1 ⇒ −x + y ≤ 1
2
y < 0 ⇒ |x| + |y| ≤ 1 ⇒ x − y ≤ 1
x > 0,
y < 0 ⇒ |x| + |y| ≤ 1 ⇒ −x − y ≤ 1
x < 0,
Lo anterior se muestra en la figura siguiente
∴ Para la región roja
Z Z
Z 0Z
f (x, y)dA =
R
−1
x+1
x+y
e
0
Z
ex+y x+1
−x−1
dydx =
−1−x
R
0
−x+1
x+y
e
Z
dydx =
e
x−x−1
−e
e−1
+ e−1
2
1
ex+y −x+1
x−1
=
e 3e−1
−
2
2
1
x−x+1
e
=
−1 e2x−1 1
e
e
e e−1
= ex −
− −
= +
0 = e−
2
2
2
2
2
∴ sumando ambos resultados obtenemos
e 3e−1 e e−1
−
+ +
= e − e−1
2
2
2
2
3
x+x−1
−e
0
Vamos ahora a intercambiar el oreden de integración
e2x+1 − e−1 dx
dx =
−1
Z
0
Z
−1
0
x−1
x+x+1
=
−1
e2x+1
e
=
− e−1 x 0−1 = −
2
2
∴ Para la región rosa
Z 1Z
Z Z
f (x, y)dA =
0
Z
Z
dx =
0
1
e − e2x−1 dx
∴ Para la región roja
Z Z
Z 1Z
f (x, y)dA =
R
0
−y+1
x+y
e
1
Z
dxdy =
y−1
ex+y −y+1
y−1
1
Z
−y+1+y
e
dy =
0
y−1+y
−e
1
Z
e − e2y−1 dy
dy =
0
0
−1 e2y−1 1
e
e
e e−1
= ey −
=e− − −
= +
2 0
2
2
2
2
∴ Para la región rosa
Z Z
Z 0Z
f (x, y)dA =
R
−1
y+1
x+y
e
Z
dxdy =
−y−1
=
0
ex+y y+1
−y−1
Z
y+1+y
dy =
−1
e2y+1
e
− ey 0−1 = −
2
2
0
e
−e
−1
e−1
+ e−1
2
=
−y−1+y
Z
0
dy =
e2y+1 − e−1 dy
−1
e 3e−1
−
2
2
∴ sumando ambos resultados obtenemos
e e−1 e 3e−1
+
+ −
= e − e−1
2
2
2
2
Ejemplo: Dibujar la región de integración y calcular la integral doble.
Z Z
f (x, y)dA donde f (x, y) = x2 y 2 y R
R
es la porción acotada del primer cuadrante situada entre las dos hipérbolas xy = 1, xy = 2 y
las lı́neas rectas y = x e y = 4x
La región donde vamos a integrar se puede apreciar en el dibujo siguiente
4
Vamos a dividirla en tres subregiones que llamaremos 1, 2 y 3 como se muestra en la figura
siguiente
∴ Para 1 tenemos que
1
√
2
Z
1
2
Z
4x
2 2
1
2
≤x≤
1
√
2
Z
x y dydx =
1
x
1
2
x
2
√1
2
y
1
x
≤ y ≤ 4x
Z √1
Z √1
5
2
2 64x
1
1
y 3 4x
(4x)3
2
− 3 dx =
− dx
x
1 dx =
1
1
3 x
3
3x
3
3x
2
2
1
1
√2
√2
64 x6 1
32
Ln(x)
6
1 =
=
− Ln(x) 1 = x −
2
3 6
3
9
3 2
− Ln(2) 32 1
1
Ln(1)
4 Ln(2) 1 Ln(2)
32 1
− Ln(2))−
−
(
Ln(1)
−
= +
− −
=
9 8
6
9 64
3
9
6
18
3
7
Ln(2) Ln(2)
+
−
18
6
3
5
∴ Para 2 tenemos que
1
Z
2
x
Z
√1
2
≤x≤1y
1
Z
2 2
x y dydx =
√1
2
1
=
1
√
2
√
1
2
Z
x
2
x
√
x2 y 2 dydx =
1
2
x2
2
x
2 3
Z 1
Z 1
(x)
y 3 x2
1
8x2
1
2
x
− 3 dx =
− 3 dx
1 dx =
3
1
1 3x
3 x
3
3x
3x
√
√
2
2
7
1
7
1
=
Ln(x) − Ln( √ ) =
0 − Ln(1) − Ln(2)
=
3
3
2
2
7 Ln(2)
7Ln(2)
=
3
2
6
7
7
dx = Ln(x) 1√1
2
3x
3
Z
≤y≤
∴ Para 3 tenemos que 1 ≤ x ≤
Z
√1
2
1
x
Z
x
2
1
x
√
2yx≤y≤
2
x
Z √2 Z √2 3
y 3 x2
8
x
8
x5
2
x
−
dx =
−
dx =
x dx =
3
3x3
3
3x
3
1
1
6
8
x6 √
8
Ln(x) − 1 2 =
3
18
3
1
1
8
1
4
4 1
4
7
Ln(2) − (8) −
Ln(1) −
= Ln(2) − +
= Ln(2) −
2
18
3
18
3
9 18
3
18
∴ Si sumamos los tres resultados anteriores tenemos que
Z Z
Z √1 Z 4x
Z 1 Z 2
Z
x
2
2 2
2 2
2 2
x y dA =
x y dydx +
x y dydx +
1
2
R
1
√
2
1
x
1
x
1
√
2
Z
2
x
x2 y 2 dydx =
x
7
Ln(2) Ln(2) 7Ln(2) 4
7
7
+
−
+
+ Ln(2) −
= Ln(2)
18
6
3
6
3
18
3
Ejemplo: Dibujar la región de integración y calcular la integral doble.
Z Z
f (x, y)dA donde f (x, y) = 3x+y y R = {(x, y) ∈ R2 |4x2 +9y 2 ≤ 36 x > 0 y > 0}
R
La región de integración se puede apreciar en el siguiente dibujo
q
En este caso vista como una región tipo 1 se tiene que 0 ≤ x ≤ 3 y 0 ≤ y ≤ 2 1 −
Z Z
Z
3
Z
q
2
1− x9
Z
(3x + y)dydx =
f (x, y)dA =
R
2
0
0
0
7
3
q
y 2 2 1− x92
3xy + 0
=
2
x2
9
∴
!
Z 3 √
x2
2(x2 − 9)
x2
3x 2 1 −
2x 9 − x2 −
+2 1−
dx =
dx =
9
9
9
0
0
3
2 27
2 3
2 x3
2
2 32
2
− 9x 0 = −
− 27 − − (9)
= −2 + 6 + 18 = 22
− (9 − x ) −
3
9 3
9 3
3
q
2
Ahora vista como una región tipo II se tiene que 0 ≤ y ≤ 2 y 0 ≤ x ≤ 3 1 − y4 ∴
Z
r
3
Z Z
Z
2
Z
f (x, y)dA =
R
3
q
2
1− y4
Z
(3x + y)dxdy =
0
0
0
2
q y2
3 1− 4
x2
3 + yx 0
dy =
2
r
Z 2
27
27
y2
y2
3 p
1−
+ 3y 1 − dy =
(4 − y 2 ) + y 4 − y 2 dy
4
4
2
0 2
0 8
3
27
y3
(4 − y 2 ) 2 2
27
8
=
4y −
−
8−
− (−4) = 27 − 9 + 4 = 22
0 =
8
3
2
8
3
Z
2
8