P 01

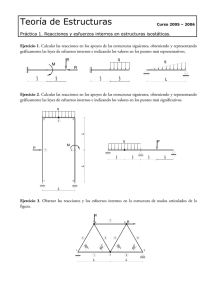
Teoría de Estructuras
Curso 2004 – 2005
Práctica 1. Reacciones y esfuerzos internos en estructuras isostáticas.
Ejercicio 1. Calcular las reacciones en los apoyos de las estructuras siguientes, obteniendo y representando
gráficamente las leyes de esfuerzos internos e indicando los valores en los puntos más representativos.
L
2
q
P1
M
q
P2
L
2
L
2
L
2
L
Ejercicio 2. Calcular las reacciones en los apoyos de las estructuras siguientes, obteniendo y representando
gráficamente las leyes de esfuerzos internos e indicando los valores en los puntos más significativos.
q
2
3
L
2
q
P
M
P
1
3
L
2
L
2
L
2
L
L
2
1
4
L
Ejercicio 3. Obtener las reacciones y los esfuerzos internos en la estructura de nudos articulados de la
figura.
P1
7
3
5
60
°
1
L
P2
6
°
60
°
60
1
4
5
2
60
°
4
2
L
3
Ejercicio 4. Obtener las reacciones en los apoyos de la estructura de la figura, calculando y representando
gráficamente las leyes de esfuerzos internos e indicando los valores en los puntos más representativos.
L
q
L
L
Ejercicio 5. Determinar las reacciones en los apoyos de las estructuras siguientes, obteniendo y
representando gráficamente las leyes de esfuerzos internos e indicando los valores en los puntos más
representativos.
2q
q
q
P
θ
L
2
L
4
L
4
L
Ejercicio 6. Resolver el pórtico de la figura, obteniendo las reacciones en sus apoyos y determinando y
representando gráficamente las leyes de esfuerzos internos junto con los valores en los puntos más
significativos.
q
q
3
2
30°
P
3
1
L
4
2
4
5
1
L
L
Ejercicio 7. Resolver la viga continua de la figura, obteniendo las reacciones en sus apoyos y determinando
y representando gráficamente las leyes de esfuerzos internos junto con los valores en los puntos más
importantes.
q
L
2
P
L
2
L
2
L
2
Ejercicio 8. Obtener las reacciones y los esfuerzos internos en la estructura de nudos articulados de la
figura.
3
9
2
3
4
6
5
2P
5
6
°
44
44°
4
7
1
1
8
2
L
4
L
Ejercicio 9. Calcular las reacciones en los apoyos de la estructura siguiente, obteniendo y representando
gráficamente las leyes de esfuerzos internos e indicando los valores en los puntos más representativos,
teniendo en cuenta que q = 1 kN/m, P1 = 10 kN, P2 = 20 kN y L = 10 m.
P2
15
9
10
P1
L
4
16
10
2q
17
11
12
11
12
13
14
q
L
P1
q
2
4
1
2
L
L
2
3
6
3
4
L
2
L
2
5
5
6
L
2
L
2
7
7
L
2
1
8
L
2
8
9
Ejercicio 10. Obtener el sistema de cargas capaz de producir las leyes de momentos flectores siguientes. En
todos los casos las curvas son parábolas de segundo grado con tangente horizontal en el vértice.
M
L
3
M
L
3
M
L
3
L
3
M
2
M
L
3
L
3