1.2 Division de un segmento de recta en una razon dada

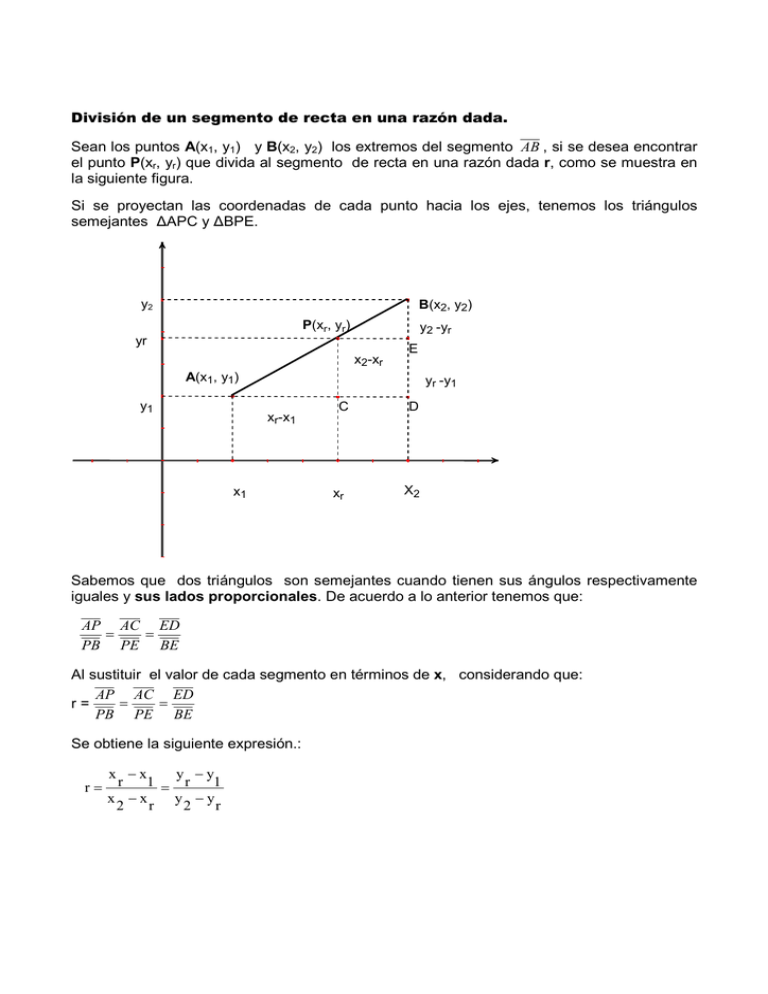
División de un segmento de recta en una razón dada.
Sean los puntos A(x1, y1) y B(x2, y2) los extremos del segmento AB , si se desea encontrar
el punto P(xr, yr) que divida al segmento de recta en una razón dada r, como se muestra en
la siguiente figura.
Si se proyectan las coordenadas de cada punto hacia los ejes, tenemos los triángulos
semejantes ∆APC y ∆BPE.
y2
B(x2, y2)
P(xr, yr)
y2 -yr
yr
x2-xr
E
A(x1, y1)
y1
yr -y1
xr-x1
x1
C
xr
D
X2
Sabemos que dos triángulos son semejantes cuando tienen sus ángulos respectivamente
iguales y sus lados proporcionales. De acuerdo a lo anterior tenemos que:
AP AC ED
=
=
PB PE BE
Al sustituir el valor de cada segmento en términos de x, considerando que:
AP AC ED
=
=
r=
PB PE BE
Se obtiene la siguiente expresión.:
r=
x −x
y −y
r
1 = r
1
x −x
y −y
2
r
2
r
Para el valor de la abscisa.
r=
Para el valor de la ordenada.
x −x
r
1
x −x
2
r
r=
y −y
r
1
y −y
2
r
r(x2-xr)= xr-x1
r( y2-yr) = yr-y1
rx2-rxr = xr-x1
ry2 - ryr = yr - y1
rx2 +x1 = xr + rxr
ry2 + y1 = yr + ryr
rx2 +x1 = xr ( 1+ r )
ry2 +y1 = yr ( 1+ r )
xr=
rx 2 + x1
(1 + r )
yr=
ry 2 + y1
(1+ r )
Por lo tanto el punto P(xr, yr), que divide a un segmento en una razón dada r se determina:
P(xr, yr)
r x 2 + x1
 (1 + r )
= 
  r y 2 + y1
, 
  (1 + r )



Un caso particular es cuando el punto P(xr, yr) se encuentran a la mitad del segmento AB ,
esto es que esta en el punto medio, esto implica que AP = PB por lo tanto la razón de
AP
semejanza
r=
es r = 1
PB
Así las fórmulas de punto medio P son:
P( xm, ym) =
(
x 1 + x 2 y1 + y 2
,
2
2
)
xm= Valor de la abscisa en el punto medio.
ym= Valor de la ordenada en el punto medio.
Ejemplos resueltos.
Ejemplo 1.
Sea A(5, 3) y B(-3, -3) los extremos del segmento AB encuentre las coordenadas del punto
P que lo divide a una razón r = 1/3
Por lo tanto P(3, 1.5)
rx + x 1
ry + y1
xr= 2
yr= 2
(1+ r )
(1+ r )
1
(−3) + 5
xr = 3
1
1+
3
xr =
xr =
xr =
−1 + 5
4
3
4
4
3
12
=3
4
1
(−3) + 3
yr = 3
1
1+
3
−1+ 3
4
3
yr =
2
4
3
yr =
6
= 1.5
4
yr =
Lo que significa que la medida de
PA es una tercera parte de la
medida de PB .
Ejemplo 2.
Los puntos A(-2, 2) y B(4, 2) son los extremos del diámetro de una circunferencia, determine
las coordenadas del centro C que divide en dos partes iguales al segmento AB .
xm=
x1 + x 2
2
ym=
y1 + y 2
2
xm =
−2+4
2
ym =
2+2
2
xm =
2
=1
2
ym =
4
=2
2
xm= 1
ym= 2
Por lo tanto las coordenadas del centro son C(1, 2).