Redes de dos puertos

REDES DE DOS PUERTOS
Las redes de dos puertos son circuitos en que se define un par de terminales
como puerto de entrada y otro par de terminales como puerto de salida.
Ejemplos de redes de dos puertos son los amplificadores y los filtros.
Una red de dos puertos puede conectarse con un generador o una carga. También
puede conectarse con otra red de dos puertos para constituir una red de dos
puertos más compleja.
Ecuaciones y parámetros de redes lineales de dos puertos
Se definen como variables de redes de dos puertos: el voltaje de entrada V1, la
corriente de entrada I1, el voltaje de salida V2, y la corriente de salida I2. De
estas cuatro variables, se seleccionan dos como variables independientes y dos
como variables dependientes.
+
+
I1
V1
−
I1
Red
lineal
I2
V2
I2
−
Las ecuaciones de una red lineal de dos puertos expresan a las dos variables
dependientes como una combinación lineal de las dos variables independientes.
Se utilizan para modelar el comportamiento de la red vista desde sus terminales.
Los cuatro coeficientes de las mencionadas combinaciones lineales se
denominan parámetros de la red. Existen diversos conjuntos de parámetros, de
acuerdo a cuáles variables se eligen como independientes.
EC2272 / Tema 3
Prof. Orlando Sucre
Abril 2008
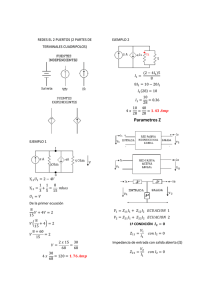
PARÁMETROS DE IMPEDANCIA
Para modelar a una red con parámetros de impedancia, o parámetros Z, se elige
como variables independientes a las corrientes, I1 e I2:
V1 = z11 I1 + z12 I 2
V1   z11 z12   I1 
V  =  z
 I 
{
2   21 z 22  
2
14243 {
V2 = z 21 I1 + z 22 I 2
[V ]
[I ]
[Z ]
Determinación de los parámetros Z
De las ecuaciones de red con parámetros Z es fácil encontrar que:
z11 =
V1
I1
z12 =
I 2 =0
V1
I2
z 21 =
I1=0
V2
I1
z 22 =
I 2 =0
V2
I2
I1 = 0
• z11 y z21 se determinan dejando el puerto de salida en circuito abierto, y
excitando el puerto de entrada. Por ello se denominan impedancia de entrada
con la salida en circuito abierto e impedancia de transferencia con la salida
en circuito abierto, respectivamente.
• z22 y z12 se determinan dejando el puerto de entrada en circuito abierto, y
excitando el puerto de salida. Por ello se denominan impedancia de salida
con la entrada en circuito abierto e impedancia de transferencia con la
entrada en circuito abierto, respectivamente.
Modelo de la red con parámetros Z
Modelo general
z11
Redes pasivas (modelo T)
z11−z12
z22
+
+
I1
V1
I2
z12 I2
−
EC2272 / Tema 3
−
−
z21 I 1
z22−z21
+
+
I1
V2
V1
−
−
Prof. Orlando Sucre
I2
z12 =z21
V2
−
Abril 2008
PARÁMETROS DE ADMITANCIA
Para modelar a una red con parámetros de admitancia, o parámetros Y, se elige
como variables independientes a los voltajes, V1 y V2:
I1 = y11V1 + y12V2
 I1   y11 y12  V1 
I  =  y
y 22  V2 
{
2   21
14243 {
I 2 = y 21V1 + y 22V2
[I ]
[V ]
[Y ]
Determinación de los parámetros Y
De las ecuaciones de red con parámetros Y es fácil encontrar que:
y11 =
I1
V1 V
y12 =
2
=0
I1
V2 V =0
y 21 =
1
I2
V1 V
y 22 =
2
=0
I2
V2
V1 = 0
• y11 y y21 se determinan con el puerto de salida en corto circuito, y excitando el
puerto de entrada. Por ello se denominan admitancia de entrada con la salida
en corto circuito y admitancia de transferencia con la salida en corto
circuito, respectivamente.
• y22 y y12 se determinan con el puerto de entrada en corto circuito, y excitando
el puerto de salida. Por ello se denominan admitancia de salida con la
entrada en corto circuito y admitancia de transferencia con la entrada en
corto circuito, respectivamente.
Modelo de la red con parámetros Y
Redes pasivas (modelo Π)
Modelo general
+
I1
V1 y11
y12 = y21
+
y12 V2
−
EC2272 / Tema 3
y21 V1
I2
y22 V2
−
Prof. Orlando Sucre
+
+
I1
V1
−
y11−y12
y22−y21
I2
V2
−
Abril 2008
PARÁMETROS HÍBRIDOS H
Para modelar a una red con parámetros híbridos H, o parámetros H, se eligen
como variables independientes la corriente de entrada I1 y el voltaje de salida V2:
V1 = h11 I1 + h12V2
V1   h11 h12   I1 
 I  = h
h22  V2 
 2  121
4243
I 2 = h21 I1 + h22V2
[H ]
Determinación de los parámetros H
De las ecuaciones de red con parámetros H es fácil encontrar que:
h11 =
V1
I1 V
h12 =
(Ω)
2
=0
V1
V2
h21 =
I1=0
I2
I1
h22 =
V2 = 0
I2
V2
(S)
I1 = 0
• h11 y h21 se determinan con el puerto de salida en corto circuito, y excitando el
puerto de entrada. Se denominan impedancia de entrada con la salida en
corto circuito y ganancia de corriente con la salida en corto circuito,
respectivamente.
• h22 y h12 se determinan con el puerto de entrada en circuito abierto, y
excitando el puerto de salida. Se denominan admitancia de salida con la
entrada en circuito abierto y ganancia inversa de voltaje con la entrada en
circuito abierto, respectivamente.
Modelo de la red con parámetros H
h11
+
V1
I1
h12 V2 −
−
h21 I1
−
EC2272 / Tema 3
+
I2
h22 V2
−
Prof. Orlando Sucre
Abril 2008
PARÁMETROS HÍBRIDOS G
Para modelar a una red con parámetros híbridos G, o parámetros G, se eligen
como variables independientes el voltaje de entrada V1 y la corriente de salida I2:
I1 = g11V1 + g12 I 2
 I1   g11 g12  V1 
V  =  g
 
 2  142
21 g 22   I 2 
43
V2 = g 21V1 + g 22 I 2
[G ]
Determinación de los parámetros G
De las ecuaciones de red con parámetros G es fácil encontrar que:
g11 =
I1
V1
g12 =
(S)
I 2 =0
I1
I 2 V =0
g 21 =
1
V2
V1
g 22 =
I 2 =0
V2
I2
(Ω)
V1 = 0
• g11 y g21 se determinan con el puerto de salida en circuito abierto, y excitando
el puerto de entrada. Se denominan admitancia de entrada con la salida en
circuito abierto y ganancia de voltaje con la salida en circuito abierto,
respectivamente.
• g22 y g12 se determinan con el puerto de entrada en corto circuito, y excitando
el puerto de salida. Se denominan impedancia de salida con la entrada en
corto circuito y ganancia inversa de corriente con la entrada en corto
circuito, respectivamente.
Modelo de la red con parámetros G
g22
+
+
I1
V1 g11
I2
g12 I 2
−
g21 V1
−
EC2272 / Tema 3
V2
−
Prof. Orlando Sucre
Abril 2008
INTERCONEXIÓN DE REDES DE DOS PUERTOS
Conexión serie-serie
+
Red a
I1
I2
V1
+
V2
Red b
−
−
I1a = I1b = I1
V1 = V1a + V1b
I 2 a = I 2b = I 2
V2 = V2 a + V2 b
[Z ] = [Z ]a + [Z ]b
[V ] = [Z ][I ]
Conexión paralelo-paralelo
Red a
+
+
V1 I1
I2 V
2
−
−
Red b
V1a = V1b = V1
I1 = I1a + I1b
V2 a = V2b = V2
I 2 = I 2 a + I 2b
[Y ] = [Y ]a + [Y ]b
[I ] = [Y ][V ]
Conexión en cascada
I2
I1
+
V1
Red a
Red b
+
V2
−
−
V1b = V2 a
I1b = −I 2 a
Otras conexiones: Serie-paralelo, paralelo-serie
EC2272 / Tema 3
Prof. Orlando Sucre
Abril 2008