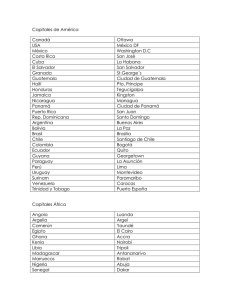
Ejercicios - Departamento de Economía

CRECIMIENTO ECONÓMICO
Ejercicios
3o Licenciatura en Economía
Profesor: Mikel Casares
Departamento de Economía
UNIVERSIDAD PÚBLICA DE NAVARRA
Curso 2011/2012
EJERCICIOS TEMA 1
Introducción.
1. En el año 1900 existían 3 países A, B y C cuyo PIB anual tenía un valor de 1
millón de $ y cuya población era de 1000 habitantes. Durante todo el siglo XX la tasa
de crecimiento anual acumulada del PIB fue un 2% cada año en el país A, un 1.5% en el
país B y un 1% en el país C. Al mismo tiempo la población aumento a una tasa anual
acumulada del 0.5% en los 3 países. Se pide:
i) Calcular el PIB, la población y el PIB per capita en el año 2000 en los 3 países.
ii) Calcular la tasa de crecimiento anual acumulada del PIB per capita durante el siglo
XX en los tres países.
iii) ¿Cuántas veces el PIB del año 1900 está contenido en el PIB del año 2000 en cada
uno de los tres países?¿Y en términos per capita?
iv) ¿Cuántas veces el PIB del país C en 2000 está contenido en el PIB del país A en
2000?¿Y en términos per capita?
2. La tasa de crecimiento instántanea de la variable temporal xt se de…ne como
@xt
xt
= @t . Comprobar el cumplimiento de las siguientes propiedades
xt =
xt
xt
xt
i) xt = @ log
@t
ii) Siendo zt = xt :yt =)
iii) Siendo zt =
xt
yt
=)
zt
zt
=
=
xt
xt
+
yt
yt
3. Existen dos variables At y Bt que están creciendo con el paso del tiempo. Los
procesos de crecimiento que describen son respectivamente At = ext A0 y Bt = (1 + x)t B0 .
i) Calcular las tasas de crecimiento instantáneas de las dos variables
At
y
Bt .
¿Son
idénticas?
ii) Supongamos que A0 = B0 = 1 y x = 0:02. Calcula los valores de A10 y B10 .
¿Cuánto han crecido estas variables en el transcurso de los 10 periodos considerados?
Ahora, calcula los valores de A100 y B100 : Comenta los resultados.
4. (Junio 2002) El producto per capita de una economía evoluciona de acuerdo al
siguiente proceso temporal
yt = 5t2 y0 :
:
Calcular su tasa de crecimiento instantánea
per capita en el periodo 20?¿Y en el 100?
1
yt
=
yt
.
yt
¿A qué tasa crecerá el producto
Representar grá…camente la evolución de la tasa de crecimiento instantánea a lo largo
del tiempo.
5. Hallar y representar grá…camente la tasa de crecimiento instántanea de las siguientes series temporales:
i) xt = 0:04
ii) yt = 0:04yt
iii) wt = 0:04
0:01wt
iv) z t = 0:01zt
0:04
Discutir la existencia o no de estado estacionario en cada uno de los procesos.
6. Funciones de producción.
Estudiar propiedades de distintas funciones de producción. Determinar si tienen o
no rendimientos constantes a escala, si su productividad marginal es decreciente en el
trabajo L y en el capital K, y si satisfacen las condiciones de Inada:
p
i) F (Kt ; Lt ) = Kt Lt
ii) G(Kt ; Lt ) = Kt Lt
iii) H(Kt ; Lt ) = Kt + Lt
p
p
iv) I(Kt ; Lt ) =
Kt + L t
2
7. (Septiembre 2002) Determinar si la siguiente función de producción es neoclásica:
F (Kt ; Lt ) = 10 +
p
Kt L t :
Justi…ca tu respuesta comprobando si la función satisface las tres propiedades de la
función de producción neoclásica.
8. (Septiembre 2003)
i) Hallar la tasa de crecimiento instantánea de la siguiente serie temporal
yt = (1 + t)2 y0
ii) ¿Existe un estado estacionario para la variable y? Describirlo si la respuesta es a…rmativa y razonar porqué no existe si la respuesta es negativa.
9. (Junio 2004) De…nir estado estacionario y poner un ejemplo.
2
10. (Septiembre 2007) Un sistema formado por dos variables temporales que siempre
toman valores positivos, xt > 0; yt > 0; evoluciona de acuerdo a las siguientes dos
ecuaciones
xt = yt e0:02t
p
yt = 0:2 yt
0:5yt
Hallar las tasas de crecimiento de xt y de yt en el estado estacionario.
11. (Septiembre 2008) Discutir si la siguiente función de producción es neoclásica o
no:
F (Kt ; Lt ) = A
p
Kt + B
p
Lt
12. (Junio 2009) Razonar si la siguiente función de producción es neoclásica o no:
Kt0:2 L0:8
t
Yt =
5
13. (Junio 2010) Hallar la tasa de crecimiento instantánea del siguiente proceso temporal
xt =
4e0:05t
:
t2
¿Hacia que tasa de crecimiento se aproxima en el (posible) estado estacionario?
3
EJERCICIOS TEMA 2
Modelos con tasa de ahorro constante y exógena
Modelo de Solow-Swan.
1. (Junio 2011) Se conocen los siguientes datos de una pequeña economía de SolowSwan con función de producción Cobb-Douglas: s = 0:18,
= 0:05, n = 0:02,
= 0:4.
Además, se conocen el capital agregado y la población en 2010: K2010 = 8500 unidades y
L2010 = 4500 habitantes. Hallar el consumo agregado en 2011.
2. La función de producción de una economía es F (Lt ; Kt ) =
p
Lt Kt . La tasa de
ahorro de sus familias es constante e igual a s. Del mismo modo el capital se deprecia a
una tasa constante
y la población crece también a una tasa constante e igual a n. Se
trata, además, de una economía cerrada sin sector público.
i) Obtener la variación instantánea del capital per capita kt en esta economía como
una función del capital corriente per capita kt (Ecuación Fundamental): Interprete el
resultado y represente grá…camente la función obtenida.
ii) Tras un análisis estadístico se ha concluído que la tasa de ahorro es s = 0:25,
su tasa de depreciación del capital es del 10% ( = 0:10), y la población crece al 2.5%
(n = 0:025). Suponiendo que en este momento inicial k0 = 1 determinar si el capital per
capita del siguiente periodo k1 será mayor o menor que el actual.
iii) ¿Qué va a ocurrir con el capital per capita desde el momento actual hasta que
se alcance una situación de equilibrio? De…nir el estado estacionario y calcular el valor
numérico del capital per capita k, el producto per capita y, y el consumo per capita c de
equilibrio. ¿A que tasa estarán creciendo estas tres variables en el estado estacionario? ¿A
qué tasa lo harán el capital agregado K, el producto agregado Y , y el consumo agregado
C?
3. Con los datos del ejercicio anterior,
i) calcule el capital per capita de la regla de oro, koro : ¿Por qué decimos que koro es el
stock de capital per capita óptimo?
ii) Obtenga la tasa de ahorro con la que se alcanzaría el nivel de capital per capita de
la regla de oro koro en estado estacionario: Represente grá…camente el resultado obtenido.
iii) ¿Podría sugerir alguna medida de política económica encaminada a la consecución
de la regla de oro?
4
4. (Septiembre 2004) i) Calcular el capital de la regla de oro en el modelo de SolowSwan con función de producción Cobb-Douglas.
ii) ¿Qué valor debería de tener la tasa de ahorro s en función de algún parámetro del
modelo para que el capital per capita del estado estacionario cumpliese la regla de oro?
p
5. (Junio 2002) La función de producción en una economía de Solow es F (Lt ; Kt ) =
Lt Kt . La tasa de ahorro de sus familias es siempre el 25% de su ingreso (s = 0:25). En
esta economía el capital se deprecia a una tasa constante del 8% ( = 0:08) y la población
crece también a una tasa constante e igual al 2% cada periodo (n = 0:02).
i) Hallar la ecuación fundamental, interpretarla y representarla grá…camente.
ii) Calcular el estado estacionario de esta economía. ¿Qué nivel tienen el capital per
capita, el producto per capita, y el consumo per capita? ¿A que tasa estarán creciendo
estas tres variables en el estado estacionario? ¿A qué tasa lo harán el capital agregado
K, el producto agregado Y , y el consumo agregado C?
iii) Hallar el capital per capita de la regla de oro koro para esta economía:
6. (Septiembre 2009) Una economía de Solow-Swan con función de producción CobbDouglas se encuentra en el estado estacionario. Supongamos que en un momento dado
se produce un aumento de la tasa de depreciación del capital , de tal forma que a partir
de entonces
0
> . Describir sus consecuencias a corto y largo plazo sobre el capital per
capita, el producto per capita, y el consumo per capita. Justi…que su respuesta apoyándose
en grá…cos explicativos.
7. Una economía de Solow-Swan con función de producción Cobb-Douglas se encuentra en el estado estacionario. Supongamos que en un momento dado se produce una
disminución de la tasa de crecimiento de la población n, de tal forma que a partir de
entonces n0 < n. Describir sus consecuencias a corto y largo plazo sobre el capital per
capita, el producto per capita, y el consumo per capita. Justi…que su respuesta apoyándose
en grá…cos explicativos.
8. (Junio 2005) Una economía de Solow-Swan con función de producción CobbDouglas F (Kt ; Lt ) = Kt L1t
se encuentra en el estado estacionario. Supongamos que
en un momento dado se produce un aumento del coe…ciente
de entonces
0<
0
, de tal forma que a partir
> . Si asumimos que el capital per capita es superior a la unidad y que
< 1:
5
i) Describir las consecuencias a corto plazo sobre el capital per capita. Justi…car la
respuesta apoyándose en un grá…co explicativo.
ii) Describir las consecuencias a largo plazo sobre el capital per capita, el producto
per capita, el consumo per capita, y el capital de la regla de oro.
iii) Representar grá…camente la evolución a lo largo del tiempo del producto per
capita desde el estado estacionario inicial hasta el estado estacionario …nal. Comentar el
(posible) crecimiento económico.
iv) ¿Cómo se va a ver afectada la tasa de crecimiento del producto agregado a corto
plazo? ¿Y a largo plazo?
9. Una economía de Solow-Swan con función de producción Cobb-Douglas Yt =
Kt L1t
viene caracterizada por los siguientes parámetros s = 0:32,
= 0:5, y
=
0:065. Además, en el momento actual se conoce que la economía se encuentra en estado
estacionario y el capital per capita es k = 16.
i) Calcular la tasa de crecimiento de la población n en esta economía.
ii) Hallar el producto per capita y consumo per capita en el estado estacionario.
iii) En el momento actual, la población es L0 = 1000 habitantes. Hallar el producto
agregado en el momento actual Y0 y el producto agregado dentro de 70 periodos Y70 .
10. En una economía de Solow-Swan conocemos que en los mercados competitivos de
trabajo y de capitales la retribución a los factores es igual a su productividad marginal.
La función de producción es F (Kt ; Lt ) = Kt L1t
. Representar grá…camente las rentas
laborales per capita y las rentas del capital per capita pagadas en esta economía. ¿Qué
ocurriría con la composición de la renta per capita si se produjera un aumento de ?
11. Una economía dispone de una tecnología de producción recogida a través de la
función de producción F (Lt ; Kt ) = Lt Kt . Asumiendo la existencia de una tasa de ahorro
constante s, una tasa de depreciación del capital constante , una tasa de crecimiento de
la población constante n, y que toda la población está empleada:
i) Obtener la tasa de crecimiento del capital per capita
kt
=
kt
:
kt
Interprete el resultado
y represente grá…camente la función obtenida.
ii) La tasa de ahorro es s = 0:20, la tasa de depreciación del capital es del 15%
( = 0:15), y la población crece al 2% (n = 0:02): Comenta la dinámica de transición
hacia el estado estacionario del capital per capita, el producto per capita, y el consumo
per capita. ¿Existe realmente un estado estacionario?
6
12. Demostrar que
F
Kt Lt
;
Lt Lt
f (kt )
kt
es una función decreciente en kt asumiendo que f (kt ) =
y F (Kt ; Lt ) es una función de producción neoclásica.
13. (Junio 2003)
i) De…nir el capital de la regla de oro, koro .
ii) Hallar su valor para una economía Solow-Swan con función de producción CobbDouglas Yt = Kt L1t
con
= 0:5, tasa de ahorro s = 0:2, tasa de crecimiento de la
población n = 0:02, y tasa de depreciación del capital
= 0:10:
iii) ¿Qué le ocurriría a koro si la tasa de ahorro aumentase a s0 = 0:3?¿Aumentaría,
disminuiría ó permanecería igual?
14. (Septiembre 2003) Una economía de Solow-Swan con función de producción CobbDouglas Yt = Kt L1t
viene caracterizada por los siguientes parámetros
= 0:5,
=
0:065, y n = 0:015. Además, en el momento actual se conoce que el capital per capita es
k0 = 4 y su tasa de crecimiento instantánea es
k0
= 0:02.
i) Calcular la tasa de ahorro s en esta economía.
ii) Hallar el capital per capita, producto per capita y consumo per capita en el estado
estacionario.
iii) En el momento actual, ¿esta economía se encuentra ya en el estado estacionario?
Razonar la respuesta y representar grá…camente el estado estacionario y la posición que
ocupa el capital per capita en el momento actual, k0 .
15. (Junio 2004) Una economía se comporta según el modelo de Solow-Swan con
función de producción Cobb-Douglas F (Kt ; Lt ) = Kt L1t
con
= 0:5. El ahorro de
esta economía es el 16% del valor de su producto (s = 0:16), la población crece un 3%
por periodo (n = 0:03), y el capital se deprecia un 7% cada periodo ( = 0:07). Se conoce
que en el momento actual la economía se encuentra en el estado estacionario.
i) Calcular el capital per capita, el producto per capita, y el consumo per capita en el
actual estado estacionario.
ii) Supongamos que esta economía recibe en el momento actual (periodo 0) una transferencia de capital físico exógena cifrada en una unidad de capital por persona. Por tanto,
el capital per capita del periodo 0, k0 , es igual al del estado estacionario más una unidad.
:
Hallar la variación instantánea para el siguiente periodo k 0 y representarla grá…camente.
Además, calcular el capital per capita, el producto per capita, y el consumo per capita
que tendrá esta economía un periodo después de recibir la ayuda (periodo 1).
7
iii) Representar grá…camente la evolución del producto per capita a lo largo del tiempo.
Comentar los efectos que la ayuda externa provoca a corto plazo y largo plazo.
16. (Junio 2009) Una economía se comporta de acuerdo al modelo Solow-Swan con
función de producción Cobb-Douglas. La tasa de ahorro es del 18%, el coe…ciente de la
función de producción es
= 0:5, la tasa de depreciación del capital es del 7% cada año
y la población crece un 2% cada año. En el año 2008, el PIB total era de 48 millones de
unidades y la población se situó en 24 millones de personas.
i) Escribir la ecuación fundamental y calcula la variación del capital per capita para
2009. ¿La economía se encuentra en estado estacionario?
ii) Representa grá…camente la ecuación fundamental y la situación en la que se encuentra la economía.
iii) Las autoridades económicas desean alcanzar un PIB total de 75 millones de
unidades en 2020. Para ello, se desea conocer la tasa de ahorro que permitiría generar
este aumento del PIB total. Asumiendo que en menos de doce años se alcanzaría el
nuevo estado estacionario, ¿cuál debería de ser la tasa de ahorro para alcanzar el objetivo
marcado?
17. (Septiembre 2004) Una economía evoluciona de acuerdo al modelo de SolowSwan con función de producción Cobb-Douglas. La tasa de ahorro es siempre del 25%
(s = 0:25), la población crece un 3% por periodo (n = 0:03), el capital se deprecia un
12% cada periodo ( = 0:12), y la función de producción Cobb-Douglas se parametriza
con
= 0:4.
i) Calcular el consumo per capita y el ahorro per capita en el estado estacionario.
ii) Calcular la tasa de crecimiento del consumo agregado en el estado estacionario.
Si en el momento actual nos encontramos en el estado estacionario y la población es
L0 = 4000 habitantes, calcular el consumo agregado dentro de 24 periodos; C24 .
iii) Calcular la productividad marginal del capital neta de depreciación en el estado
estacionario de esta economía. ¿Cómo le afectaría una caída de la tasa de crecimiento de
la población?
18. (Septiembre 2005) Una economía de Solow-Swan con función de producción CobbDouglas F (Kt ; Lt ) = Kt L1t
tiene dos unidades de capital per capita en el año 2005
(k2005 = 2). Los parámetros de la estructura de esta economía toman los siguientes
valores numéricos
= 0:5, s = 0:2,
= 0:08, y n = 0:03.
8
i) Calcular el capital per capita, el consumo per capita y el producto per capita que
tendrá esta economía en el año 2006.
ii) Hallar el capital per capita del estado estacionario. Representarlo grá…camente
junto a la posición que ocupa la economía en 2005.
iii) Si la población de esta economía en el año 2005 es de 2.4 millones de habitantes,
hallar el producto agregado que se obtendrá en el año 2006.
19. (Septiembre 2007) Una economía se comporta tal y como describe el modelo
de Solow-Swan sin progreso tecnológico con función de producción Cobb-Douglas Yt =
Kt L1t
con
= 0:5, tasa de ahorro constante en s = 0:18, tasa de depreciación del capital
constante en
= 0:10, y tasa de crecimiento de la población constante en n = 0:02. Se
ha comprobado que esta economía se encuentra en estado estacionario.
i) Hallar el capital per capita, producto per capita y consumo per capita. ¿Cuál es su
tasa de crecimiento?¿Y la de las variables agregadas?
ii) Supongamos que se desea alcanzar un producto per capita a largo plazo de 2
unidades, y = 2:0. De…nir el valor de la tasa de ahorro que permitiría conseguir ese
objetivo y poner un par de ejemplos de políticas que permitieran alcanzar esa tasa de
ahorro.
iii) ¿Cuál será la evolución del consumo per capita a corto y largo plazo si se modi…ca
la tasa de ahorro tal y como plantea el apartado anterior?
20. (Septiembre 2008) El capital per capita de una economía de Solow-Swan con
función de producción Cobb-Douglas F (Kt ; Lt ) = Kt Lt1
en el año 2007 ha sido k2007 =
2:25. Los parámetros de la estructura de esta economía tienen los siguientes valores
numéricos
= 0:5, s = 0:2,
= 0:08, y n = 0:02.
i) Escribir la ecuación fundamental, interpretarla económicamente y calcular el capital
per capita, el consumo per capita y el producto per capita que tendrá esta economía en
el año 2008.
ii) Hallar el capital per capita del estado estacionario. Representarlo grá…camente
junto a la posición que ocupó la economía en 2007. Comenta la evolución que se espera
para el capital per capita en futuros años.
iii) Si la población de esta economía en el año 2007 fue de 2.4 millones de habitantes,
hallar el consumo agregado que se obtendrá en el año 2008.
21. (Junio 2010) El capital per capita de una economía de Solow con función de
9
producción Cobb-Douglas tiene una tasa de crecimiento del 2% para el siguiente periodo.
Su tasa de ahorro se situa en el 16%, el capital se deprecia un 8% cada periodo, el
coe…ciente
es igual a 0.5 y no hay crecimiento de la población.
i) Hallar el capital per capita del periodo actual
ii) Representar grá…camente la situación en la que se encuentra la economía a través
de su ecuación fundamental y describir la evolución que seguirá hasta alcanzar el estado
estacionario.
iii) Si la población se situa en 12 millones de habitantes, hallar los niveles del capital
agregado, producto agregado, y consumo agregado en el estado estacionario.
Modelo de Solow-Swan con progreso tecnológico.
22. (Mayo 2010) Una economía evoluciona según establece el modelo Solow-Swan con
una función de producción Cobb-Douglas a la que se le incorpora progreso tecnológico
potenciador del trabajo y está caracterizada por los siguientes valores numéricos de sus
parámetros:
= 0:5, s = 0:25,
= 0:05, n = 0:03, x = 0:02. En el momento actual,
se conoce que esta economía tiene 8 millones de habitantes, un consumo agregado de 16
millones de unidades y su variable tecnológica tiene un valor igual a 1.5.
i) Escribir la ecuación fundamental y hallar la variación del capital por unidad de
trabajo efectivo para el siguiente periodo.
ii) Calcular el consumo agregado para el periodo siguiente y su tasa de crecimiento.
iii) Hallar el capital por unidad de trabajo efectivo en el estado estacionario. ¿Se
encuentra esta economía en estado estacionario? Representar gra…camente la situación
actual y describir la evolución que tendrá esta economía en el futuro. ¿A qué tasa crecerá
el consumo agregado en el estado estacionario?
23. (Junio 2009) Se sabe que una economía evoluciona segun establece el modelo
Solow-Swan con progreso tecnológico potenciador del trabajo con los siguientes valores
numéricos de sus parámetros:
= 0:5, s = 0:24,
= 0:08, n = 0:025; x = 0:015. El
capital per capita inicial es k0 = 2:94 y la variable tecnológica toma un valor A0 = 1:5:
i) Escribir la ecuación fundamental, hallar la variación del capital por unidad de
trabajo efectivo para el siguiente periodo y representar el resultado grá…camente.
ii) Obtener los valores del capital por unidad de trabajo efectivo y consumo por unidad
de trabajo efectivo en el estado estacionario.
10
iii) Hallar el producto per capita en los periodos 0 y 1:¿A qué tasa está creciendo?
¿A qué tasa crecerá a largo plazo? Representar grá…camente la evolución esperada para
la tasa de crecimiento del PIB per capita a lo largo del tiempo y comentar el grá…co.
24. Existen dos economías que comparten las características propias del modelo de
Solow-Swan (tasa de ahorro constante s, tasa de depreciación del capital constante ,
tasa de crecimiento de la población constante n) junto con una función de producción
de tipo Cobb-Douglas con progreso tecnológico potenciador de trabajo F (Kt ; At Lt ) =
Kt (At Lt )1
. Su única diferencia es que en el primer país la tecnología se mantiene
constante a lo largo del tiempo At = A0 mientras que en el segundo país la tecnología
crece a una tasa positiva y constante x, At = ext A0 . Se pide:
i) Calcular la tasa de crecimiento del capital por unidad de trabajo efectivo
b
kt
=
b
kt
b
kt
en las dos economías. Represéntalas grá…camente. (Recuerda que el capital por unidad
de trabajo efectivo es b
kt = Kt ).
At Lt
ii) Calcula y compara el capital por unidad de trabajo efectivo en el estado estacionario
b
k para las dos economías. Representa grá…camente el estado estacionario. ¿A qué tasa
estarán creciendo en el estado estacionario?¿A qué tasa lo harán el capital per capita k, el
capital agregado K, el producto por unidad de trabajo efectivo yb, el producto per capita
y, y el producto agregado Y en cada una de las economías??
25. Existe una economía que disfruta de un crecimiento económico descrito por
el modelo de Solow-Swan con crecimiento tecnológico. Su función de producción es
p
F (At Lt ; Kt ) = At Lt Kt . Se conoce también que la tasa de ahorro es s = 0:20, la
depreciación del capital es del 8% ( = 0:08) y la población crece a un ritmo del 2% en
cada periodo (n = 0:02). En cuanto a la tecnología, crece a una tasa constante del 1%
por periodo (x = 0:01): Se sabe que en el momento actual A0 = 4 y k0 = 9.
i) Calcular el capital por unidad de trabajo efectivo en este periodo b
k0 , su incremento
:
b
k0 , y su tasa de crecimiento
b
k0
=
b
k0
.
b
k0
(Pista: acuérdate que b
k0 =
K0
A0 L0
=
k0
)
A0
ii) Calcular el capital y el producto por unidad de trabajo efectivo en el estado esta-
cionario. Representa grá…camente el estado estacionario y haz referencia a la situación
actual de la economía. Comenta el proceso de convergencia hacia el estado estacionario.
iii) Calcular la variación del capital per capita en este periodo k 0 , y su tasa de crecimiento
k0
=
k0
.
k0
Comprobar que
k0
=
A
+
b
k0 .
26. Dos países, el país i y el país j, un crecimiento económico descrito de acuerdo
11
al modelo de Solow-Swan con una función de producción Cobb-Douglas con tecnología
potenciadora de trabajo. Ambos países tienen la misma tasa de ahorro s, el mismo
crecimiento de la población n; la misma tasa de depreciación del capital , y la misma
tasa de crecimiento del componente tecnológico x. Además tienen la misma población
Lit = Ljt . Su unica diferencia radica en que su nivel inicial tecnológico es distinto. En
concreto, el país i tiene un nivel tecnológico igual a dos veces el del país j con lo que los
productos agregados de los dos países serán Yit = Kit (Ait Lit )1
e Yjt = Kjt (Ajt Ljt )1
donde Ait = 2Ajt . Sabiendo que ambos países se encuentran en el estado estacionario
kit yit
i) Calcular los ratios
e
:
kjt yjt
ii) La retribución a los factores productivos (trabajo y capital) es igual a su productividad marginal. Suponiendo que exista libertad de movimiento de trabajadores y
capitales, ¿existe algún incentivo a mover mano de obra o capitales de un país a otro?¿Qué
consecuencias pueden tener estos movimientos a corto y largo plazo?
27. (Junio 2008) Una economía se encuentra en un estado estacionario en el que crece a
una tasa constante, periodo tras periodo, tal y como se establece en el modelo Solow-Swan
con progreso tecnológico potenciador del trabajo y función de producción Cobb-Douglas,
Yt = Kt (At Lt )1
. Los valores numéricos de los parámetros que describen esta economía
son s = 0:20, n = 0:02,
= 0:07,
= 0:40 y la tecnología mejora a una tasa constante e
igual al 1.5% (x = 0:015). Actualmente la variable tecnológica toma el valor A0 = 5.
i) Hallar el capital per capita y el producto per capita del momento actual.
De repente, esta economía sufre un desgraciado terremoto con efectos muy devastadores que provocan la destrucción del 20% del stock de capital.
ii) Calcular la tasa de crecimiento del producto per capita para el periodo siguiente a
partir del terremoto.
iii) Representar grá…camente los efectos del terremoto sobre la variación del capital
k. Comentar el grá…co.
por unidad de trabajo efectivo, b
28. (Septiembre 2002) Existe una economía caracterizada por el modelo de Solow-
Swan con progreso tecnológico potenciador del trabajo. Su función de producción es
F (At Lt ; Kt ) = Kt (At Lt )1
. En esta economía sabemos que la tasa de ahorro es s =
0:15, la depreciación del capital es del 4% por periodo ( = 0:04) y la población crece a
un ritmo constante del 2% en cada periodo (n = 0:02). En la función de producción, se
conoce que
= 0:5. En cuanto a la tecnología, crece a una tasa constante del 1.5% por
12
periodo (x = 0:015).
i) Calcular el capital por unidad de trabajo efectivo en el estado estacionario. Representa grá…camente el estado estacionario.
ii) Hallar el valor numérico de las tasas de crecimiento en el estado estacionario del
capital, el producto, y el consumo por unidad de trabajo efectivo, del capital, el producto,
y el consumo per capita, y del capital agregado, el producto agregado, y el consumo
agregado.
iii) Si en el momento actual b
k0 = 1 y A0 = 1:5, ¿Qué valor tendrá el capital por
unidad de trabajo efectivo del periodo siguiente, b
k1 ?¿Y el capital per capita del periodo
siguiente, k1 ?¿Qué valores toman las tasas de crecimiento
b
k0
y
k0 ?
29. (Junio 2003) Una economía evoluciona de acuerdo al modelo Solow-Swan con
progreso tecnológico potenciador del trabajo incorporado. Su función de producción es
Cobb-Douglas Yt = Kt (At Lt )1
con
= 0:5. La tasa de ahorro es del 20% (s = 0:2), la
tasa de depreciación del capital es del 6% ( = 0:06), la población crece al 3% (n = 0:03)
y la tecnología tiene un crecimiento constante del 1% (x = 0:01).
i) Hallar el capital per capita en unidades de trabajo efectivo en el estado estacionario
b
k. Representar grá…camente el estado estacionario.
ii) En el momento actual se conoce que el nivel tecnológico es A0 = 1:2, y el capital
per capita es k0 = 4:8. Hallar el capital per capita del siguiente periodo k1 ¿Está economía
se encuentra ya en el estado estacionario?
iii) Sabiendo que en el momento actual el consumo agregado es C0 = 860, hallar el
consumo agregado dentro de 5 periodos, C5 .
30. (Mayo 2011) Una economía evoluciona según se establece en un modelo SolowSwan con progreso tecnológico potenciador del trabajo. Tanto la variable tecnológica
como la población crecen a una tasa del 2%, el capital se deprecia a una tasa del 6% y
la función de producción es Cobb-Douglas con
= 0:5. En el momento actual (periodo
0) se conoce que la variable tecnológica tiene un valor A0 = 1:4, el capital per capita es
k0 = 3:15, y el capital por unidad de trabajo efectivo tiene una variación positiva de 0.08
unidades para el siguiente periodo.
i) Calcular la tasa de ahorro de esta economía.
ii) Hallar el valor númerico del capital por unidad de trabajo efectivo en el estado estacionario. Representar grá…camente el estado estacionario y la situación actual en la que
se encuentra la economía. Describir el proceso de transición hacia el estado estacionario.
13
iii) Hallar la tasa de crecimiento del producto per capita en el momento actual y
describir grá…camente la evolución que va a seguir esta tasa de crecimiento a lo largo del
tiempo. ¿Qué determina el crecimiento económico a largo plazo en esta economía?
31. (Septiembre 2005) Dos economías, A y B, son muy parecidas y están caracterizadas
por el modelo de Solow-Swan con la misma función de producción Cobb-Douglas con
progreso tecnológico potenciador del trabajo, F (Kt ; At Lt ) = Kt (At Lt )1
. Su única
diferencia se encuentra en la tasa de crecimiento de la población. La economía A tiene
una tasa de crecimiento de la población mayor que la de la economía B, nA > nB .
Suponiendo que ambas economías se encuentran actualmente en su equilibrio a largo
plazo (estado estacionario):
i) Comparar el nivel del producto per capita de ambas economías en el periodo actual.
¿Son iguales?. ¿Tienen la misma tasa de crecimiento?
ii) La diferencia entre los dos productos per capita ytA
ytB , ¿crece, decrece ó se
mantiene a lo largo del tiempo?
32. (Junio 2007) Una economía se comporta de acuerdo al modelo Solow-Swan con
progreso tecnológico potenciador del trabajo recogido por la función de producción CobbDouglas F (Kt ; At Lt ) = Kt (At Lt )1
con
= 0:5. Se conoce que la población crece un
2% por periodo (n = 0:02), el capital se deprecia un 8% cada periodo ( = 0:08) y la
variable tecnológica mejora crece un 2% por periodo (x = 0:02). También se conoce que
en el estado estacionario de esta economía el producto por unidad de trabajo efectivo es
yb = 1:5.
i) Hallar la tasa de ahorro, s.
ii) En la actualidad, el capital per capita tiene un valor de k0 = 6 unidades mientras
que la variable tecnológica toma un valor A0 = 3. Hallar la variación del capital por
unidad de trabajo efectivo, b
k o , y mostrarla grá…camente comparándola con la obtenida
en el estado estacionario. ¿Qué evolución cabría esperar a corto y largo plazo para b
k?
iii) Calcular la tasa de crecimiento del producto per capita para el siguiente periodo,
yo ,
y compararla con la del estado estacionario.
33. Suponed que la función de producción de una economía de Solow-Swan con
progeso tecnológico potenciador del trabajo es F (Kt ; At Lt ; Tt ) = Kt (At Lt ) Tt1
; ;1
> 0, y
+
con
< 1. La cantidad producida depende del número de máquinas
14
(Kt ), el trabajo efectivo (At Lt ), y la cantidad de metros cuadrados de tierra en la que
producir (Tt ).
i) Estudiar si la función de producción es neoclásica.
ii) Supongamos que la tierra es una cantidad constante (Tt = T ), supuesto razonable mientras el ser humano no encuentre otro planeta en el que producir, y la variable
tecnológica crece a la misma tasa constante
At
= x > 0 durante todos los periodos.
Obtener la Ecuación Fundamental e interpretarla.
iii)¿Es posible alcanzar un estado estacionario? En caso a…rmativo, ¿a qué tasa crecería el producto per capita?
Modelo de Harrod-Domar.
34. (Septiembre 2009) Una economía sin sector público ni resto del mundo tiene una
función de producción Yt = minfKt ; 3Lt g, una tasa de ahorro siempre al 15%, tasa de
depreciación constante en el 5%, la población siempre trabaja y el número de habitantes
crece un 2% cada perido.
i) Si el stock de capital per capita en el momento actual es k0 = 2, hallar el capital per
capita, producto per capita y el consumo per capita alcanzados en el siguiente periodo.
ii) Representar grá…camente la situación actual, mostrando como se obtiene la variación
del capital per capita.
35. En una economía que se comporta según el modelo de Harrod-Domar la función de
producción es F (Kt ; Lt ) = min(AKt ; BLt ). La tasa de ahorro s es constante, la población
crece a una tasa constante n, y el capital se desprecia a una tasa constante . En un
momento inicial se sabe que sA < n + .
i) Representa grá…camente la tasa de crecimiento del capital per capita de esta economía.
Con estos datos, ¿qué va a ocurrir con el stock de capital per capita k, crecerá o decrecerá?¿Hacia que situación se tiende en el estado estacionario?
ii) Ahora supongamos que la tasa de ahorro cambia de tal forma que sube hasta s0
con lo que la desigualdad anterior pasa a ser s0 A > n + . Describe lo que crees que va
a ocurrir en esta economía (en términos del capital y el producto per capita) a corto y
largo plazo.
36. Una economía de Harrod-Domar tiene una función de producción de proporciones
…jas F (Kt ; Lt ) = min(AKt ; BLt ) que determina la relación capital trabajo de e…ciencia
k=
B
.
A
Se conoce que para esta economía sA > n + .
15
i) Comenta los efectos a corto y largo plazo de un aumento de A hasta A0 > A, manteniendo B constante: ¿Aumentará el número de máquinas ociosas o el de trabajadores
desempleados?
37. (Junio 2011) Existe una economía que evoluciona de acuerdo al modelo de HarrodDomar con una función de producción de coe…cientes …jos de Leontief F (Kt ; Lt ) =
min(AKt ; BLt ). Se sabe que esta economía tiene una tasa de ahorro del 20% (s = 0:2),
su tasa de depreciación del capital es del 10% ( = 0:10), y la población crece al 2.5%
(n = 0:025). Además las constantes de la función de producción son A = 1 y B = 2.
i) Representar grá…camente el estado estacionario. Calcular el capital, el producto y
el consumo per capita. ¿Existe alguna situación ociosa de los factores productivos, capital
y trabajo?
ii) Supongamos que hay una mejora tecnológica por la que cambian las constantes de
la función de producción a A0 = 2 y B 0 = 4. Escribe la ecuación fundamental y describe
los efectos que observaremos a corto plazo.
iii) Tras la mejora tecnológica, ¿qué niveles se alcanzarán para el el capital, el producto
y el consumo per capita en el nuevo estado estacionario? Representar grá…camente el
viejo y nuevo estado estacionario en función del capital per capita y describir cómo será
la transición entre uno y otro.
38. Pensemos en una economía representada por el modelo de Harrod-Domar y donde
sA = n + . Caracteriza las posibles situaciones de equilibrio a largo plazo apoyándote en
algún tipo de representación grá…ca. ¿Qué determina el estado estacionario?¿Crees que
el estado estacionario es un equilibrio estable? Razona tus respuestas.
39.- (Septiembre 2002) En una economía de Harrod-Domar con función de producción
de Leontief Yt = min(AKt ; BLt ) y con sA > n + se produce un aumento del coe…ciente
B en la función de producción, de tal forma que ahora B 0 > B. Comenta los efectos que
este cambio provoca sobre el capital per capita k, el producto per capita y, y el consumo
per capita c en el estado estacionario.
40. (Junio 2003) En una economía de Harrod-Domar con función de producción de
Leontief Yt = min(AKt ; BLt ) y con sA > n +
se produce una disminución en la tasa
de crecimiento de la población, de tal forma que ahora n0 < n. Comenta los efectos en
el estado estacionario sobre el capital per capita k, el número de máquinas ociosas per
capita k
k, el producto per capita y, y el consumo per capita c.
16
41. (Junio 2008) Pensemos en una economía representada por el modelo de HarrodDomar con función de producción Yt = minf4Kt ; 3Lt g en la que casualmente se cumple
la siguiente relación entre sus parámetros sA = n + . La dotación inicial de capital per
capita es igual a la unidad, k0 = 1.
i) Representa grá…camente la situación actual y describe como será la transición hacia
el estado estacionario.
ii) ¿Qué valores numéricos tendrán el capital per capita, el producto per capita y el
número de máquinas ociosas per capita en el estado estacionario?
42. Un país africano (de cuyo nombre no quiero acordarme) se encuentra sumido en el
subdesarrollo. Su PIB en 2004 fue de 8000 millones de $ y su población en ese momento
era de 5 millones de personas. La población crece a una tasa constante del 3% cada
año. Pensemos que somos gestores del Banco Mundial y deseamos ayudar al progreso
económico de este país. Para ello utilizamos el modelo de Harrod-Domar con su hipótesis
del acelerador (como vino siendo práctica habitual en el Banco Mundial). El acelerador
para este país africano se calcula que es A = 0:25. El gasto en inversión (asumiendo que
no hay depreciación del capital) estimado para 2005 es de 640 millones de $.
i) Calcular el producto per capita esperado para el año 2005.
Ahora supongamos que conseguimos …nanciación para incrementar la inversión llevada
a cabo en este país. Tenemos que determinar la cuantía de la ayuda extranjera destinada
a aumentar la inversión en este país. Nuestro objetivo es cubrir el dé…cit …nanciero
existente para que el producto per capita crezca al 2% cada año.
ii) ¿Cual es la inversión requerida?¿Qué parte de la inversión provendrá de la ayuda
extranjera?
iii) Si el modelo funcionara y las condiciones se mantuvieran durante 10 años, ¿cuál
sería el producto per capita en 2015?
iv) Atendiendo a la realidad, ¿esperas que esta política de ayuda al desarrollo sea
efectiva?
43. (Junio 2005) Una organización gubernamental internacional va a decidir la ayuda
destinada al desarrollo de un país pobre aplicando el enfoque del de…cit …nanciero. Se
desea que la tasa de crecimiento del producto per capita para el año que viene sea del
3%. La población crece un 5% cada año, el producto agregado (PIB) de este año es
de 2300 millones de euros y la inversión nacional esperada para el año que viene es de
17
200 millones de euros. La productividad marginal del capital (acelerador) es igual a la
constante A = 0:32.
i) Calcular la tasa de inversión requerida.
ii) Calcular la inversión requerida.
iii) Hallar el de…cit …nanciero que determinará la ayuda concedida a este país.
iv) Comentar las implicaciones que ha tenido la utilización de este enfoque en la
e…cacia de los programas de ayuda al desarrollo.
44. (Mayo 2010) Hallar el de…cit …nanciero en una economía con una inversión esperada de 250 millones de dólares, una tasa de crecimiento deseada del PIB per capita
del 2%, un crecimiento de la población del 4% cada año, un coe…ciente de aceleración
A = 0:4 y un PIB del año precedente igual 3000 millones de dolares. (Asumir que la tasa
de depreciación del capital es cero).
18
EJERCICIOS TEMA 3
Modelos neoclásicos de optimización: El modelo de Ramsey.
1. (Junio 2010) Una economía evoluciona según establece el modelo de Ramsey con
familias productoras, horizonte temporal in…nito, función de utilidad isoelástica y función
de producción Cobb-Douglas. En el momento actual el consumo per capita es de c0 =
2 unidades y el capital per capita alcanza el nivel k0 = 9 unidades. Los parámetros
estructurales de esta economía tienen los siguientes valores numéricos: n = 0:02,
= 0:04,
= 0:6 y
= 0:06,
= 2:0.
i) Calcular el capital per capita y el consumo per capita para el siguiente periodo.
ii) Obtener el capital per capita y el consumo per capita en el estado estacionario
hacia el que se dirige la economía.
iii) Dibujar el diagrama de fases y explicar la evolución que va a seguir la economía a
corto y largo plazo.
2. (Septiembre 2005) Cambio de la tasa de depreciación del capital, .
En una economía de Ramsey con familias productoras, horizonte temporal in…nito,
función de producción Cobb-Douglas F (Lt ; Kt ) = Kt L1t
ticidad constante U (ct ) =
c1t
1
1
y función de utilidad de elas-
, se produce una disminución en la tasa de depreciación
del capital de tal forma que a partir de ahora ésta vale
0
< .
i) Hallar los posibles estados estacionarios que se obtienen con
0
y con . Represen-
tarlos en el diagrama de fases.
ii) Comentar los efectos de la disminución en la tasa de depreciación del capital sobre
el capital y el consumo per capita en el nuevo estado estacionario al que se aproxima la
única trayectoria óptima.
iii) ¿Cómo afecta la disminución de la tasa de depreciación del capital a la tasa de
ahorro en dicho estado estacionario? (Asumir
> n).
3. (Junio 2002) Cambio de la tasa de crecimiento de la población, n.
En una economía de Ramsey con familias productoras, función de producción CobbDouglas F (Lt ; Kt ) = Kt L1t
c1t
1
0
1
y función de utilidad de elasticidad constante U (ct ) =
, se produce un incremento en la tasa de crecimiento de la población desde n hasta
n de tal forma que a partir de ahora ésta vale n0 > n.
i) Representar el diagrama de fases y las posiciones de los estados estacionarios que
se obtienen con n y con n0 .
19
ii) Comentar los efectos del aumento de la tasa de crecimiento de la población sobre
el capital y el consumo per capita en el nuevo estado estacionario al que se aproxima la
única trayectoria óptima.
iii) ¿Cómo afecta el aumento de la tasa de crecimiento de la población a la tasa de
crecimiento del producto per capita en dicho estado estacionario?¿Y a la del producto
agregado?
iv) ¿Cómo afecta el aumento de la tasa de crecimiento de la población a la tasa de
ahorro en dicho estado estacionario?
4. (Septiembre 2002) En una economía de Ramsey con familias productoras, con
función de producción Cobb-Douglas F (Lt ; Kt ) = Kt Lt1
elasticidad constante U (ct ) =
c1t
1
1
y con función de utilidad de
:
i) Hallar las ecuaciones dinámicas del consumo y el capital per capita.
ii) Representar el diagrama de fases.
iii) Asumiendo el valor de los siguientes parámetros:
n = 0:02 y
= 0:5,
= 2:0,
= 0:04,
= 0:06, calcular los valores numéricos de los tres estados estacionarios
resultantes e introducirlos valores en el diagrama de fases.
iv) En el momento actual se conoce que k0 = 1 y c0 = 0:6, ¿Qué valor tendrán el
capital y el consumo per capita en el siguiente periodo?¿A qué tasa estarán creciendo (o
decreciendo)?
5. (Junio 2003) Una economía con mercados competitivos, función de producción
Cobb-Douglas F (Lt ; Kt ) = Kt L1t
c1t
1
1
y función de utilidad de elasticidad constante U (ct ) =
, se comporta de acuerdo al modelo de Ramsey con horizonte temporal in…nito.
i) A partir del comportamiento optimizador de la empresa competitiva que maximiza
bene…cios, hallar las ecuaciones dinámicas que de…nen la demanda de capital y la demanda
de trabajo.
ii) A partir de los supuestos del modelo, hallar la ecuación dinámica del capital per
capita.
iii) A partir del comportamiento optimizador de la familia consumidora que maximiza
utilidad, hallar la ecuación dinámica del consumo per capita.
iv) Relacionar las ecuaciones dinámicas obtenidas en los apartados anteriores con
aquellas resultantes de una economía con familias productoras.
6. (Septiembre 2003) En una economía de Ramsey con familias productoras, hori20
zonte temporal in…nito, función de producción Cobb-Douglas, y función de utilidad de
elasticidad constante U (ct ) =
c1t
1
1
, se conoce que la tasa de preferencia intertemporal
es del 4% ( = 0:04), la tasa de crecimiento de la población es el 3% (n = 0:03), y la tasa
de depreciación del capital es del 6% ( = 0:06). También se conoce que
función de producción y
= 0:5 en la
= 2 en la función de utilidad.
i) A partir de las ecuaciones dinámicas del capital per capita y el consumo per capita,
hallar los tres estados estacionarios (con sus valores numéricos) y representar grá…camente
el diagrama de fases.
ii) Las dotaciones iniciales de capital per capita y consumo per capita son k0 = 49 y
c0 = 2. Calcular k1 y c1 .
iii) El punto que representa la dotación inicial (k0 ; c0 ), ¿se encuentra en la única
trayectoria óptima de aproximación al estado estacionario? Razonar la respuesta.
7. Mejora tecnológica (Septiembre 2007).
En una economía de Ramsey con familias productoras la función de utilidad es de
elasticidad constante U (ct ) =
c1t
1
1
y la función de producción es F (Kt ; Lt ) = AKt L1t
.
En un momento dado del tiempo se produce un aumento del valor de A hasta un nivel
superior A0 > A, que se mantiene de forma inde…nida en el tiempo.
i) Escribir las ecuaciones dinámicas, representar el diagrama de fases y la posición del
estado estacionario al que se aproxima la única trayectoria óptima para los niveles inicial
A y …nal A0 .
ii) Hallar el valor del capital per capita en el estado estacionario al que se aproxima
la única trayectoria óptima en función de los parámetros del modelo. Hallar también el
producto per capita y el consumo per capita que se obtienen en este estado estacionario.
Comparar los niveles obtenidos con la tecnología inicial A y con la tecnología …nal A0 .
iii) ¿Cómo afecta la mejora del parámetro tecnológico A a la productividad marginal
del capital en dicho estado estacionario? ¿Y a la tasa de ahorro?
8. Trayectorias dinámicas óptimas.
Para una economía de Ramsey con los siguientes datos
= 0:25, n = 0:02,
= 0:05
y con la ayuda de un ordenador,
i) Calcular las trayectorias dinámicas del capital per capita kt y del consumo per
capita ct a partir de un momento inicial en el que toman los valores k0 = 1 y c0 = 0:5
(tomar el valor exacto de
= 0:54793225316). ¿Qué ocurrirá al cabo de 100 periodos
21
con sus valores k100 y c100 ? ¿A que estado estacionario nos aproximamos? Represéntalo
:
:
grá…camente. (Pista: recuerda que kt+1 = kt + kt y ct+1 = ct + ct ).
ii) Ahora partamos de unos valores iniciales k0 = 1 y c0 = 0:4. ¿Donde acabaremos
al cabo de 100 periodos?¿Ocurrirá esto mismo si tuviéramos en cuenta la condición de
transversalidad?
iii) Finalmente supongamos que los valores iniciales fueran k0 = 1 y c0 = 0:6. ¿Hacia
donde se moverá la economía con el paso del tiempo?¿Cambiaría este resultado si nuestro
horizonte temporal fuera …nito?
9. Problema de función de utilidad logarítmica.
En una economía de Ramsey existen mercados competitivos de trabajo, capital y
bonos. La función de producción de las empresas es neoclásica del tipo Cobb-Douglas
F (Kt ; Lt ) = Kt L1t
y la función de utilidad de la familia representativa es logarítmica
U (ct ) = log(ct ):
i) Hallar las ecuaciones de demanda de trabajo y demanda de capital de la empresa
competitiva representativa maximizadora de bene…cios. Expresar estas ecuaciones dependiendo de variables per capita.
ii) Hallar las ecuaciones dinámicas de capital y consumo per capita que se obtienen al
resolver el problema de optimización de la familia representativa con horizonte temporal
in…nito.
iii) Representar el diagrama de fases utilizando conjuntamente los resultados de i) y
ii) (asumir
> n).
iv) Comparar el resultado con el que se obtiene para la economía competitiva con
función de utilidad de elasticidad constante U (ct ) =
c1t
1
1
.
v) Observando la ecuación que representa la evolución dinámica del consumo, ¿qué
valor del parámetro
en la función de utilidad con elasticidad constante nos permite
obtener esa misma ecuación?¿Cómo afecta la función de utilidad logarítmica a la evolución
dinámica del consumo?
vi) Hallar el valor del capital per capita que se obtiene en el estado estacionario al que
se aproxima la única trayectoria óptima en función de los parámetros del modelo. Hallar
también el producto per capita y el consumo per capita que se obtienen en este estado
estacionario.¿Cómo afecta la función de utilidad logarítmica a este estado estacionario?
10. (Junio 2005) Una economía de Ramsey con mercados competitivos de trabajo,
capital y bonos, función de producción Cobb-Douglas y función de utilidad de elasticidad
22
constante con horizonte temporal in…nito está caracterizada por los siguientes valores de
sus parámetros:
= 0:35,
= 0:06,
= 0:04, n = 0:02 y
= 2:0.
i) Hallar los valores del capital per capita y el consumo per capita del estado estacionario hacia el que se aproxima la única trayectoria óptima. Representar el diagrama
de fases.
ii) En el momento actual, el consumo per capita es c0 = 1 y el capital per capita es
k0 = 5. Hallar el consumo per capita y el capital per capita del siguiente periodo, c1 y
k1 . Representa la situación de la economía en el diagrama de fases e indica como va a
evolucionar.
iii) Utilizar la condición de arbitraje y la de demanda de capital de la empresa para
calcular el tipo de interés de los bonos, r0 , y la productividad marginal del capital,
f 0 (k0 ). Comprobar que la rentabilidad del activo físico coincide con la del activo …nanciero
(condición de arbitraje).
11. (Junio 2004) Se desea estudiar una economía de Ramsey con familias productoras,
función de utilidad de elasticidad constante U (ct ) =
producción Cobb-Douglas F (Kt ; Lt ) = Kt L1t
con
c1t
1
1
con
= 4 y función de
= 0:5. Esta economía queda
caracterizada además por los siguientes valores de sus restantes parámetros: la tasa de
crecimiento de la población es del 1% por periodo (n = 0:01), la tasa de depreciación del
capital es del 6% por periodo ( = 0:06), y la tasa de preferencia intertemporal es el 5%
( = 0:05).
i) Calcular los tres puntos (k; c) candidatos a estados estacionarios y explicar porqué
la única trayectoria óptima se dirige exclusivamente hacia uno de ellos.
ii) Representar el diagrama de fases en el que aparezcan representados los resultados
del apartado anterior y la única trayectoria óptima. Explicar la evolución esperada para
el capital y el consumo per capita.
iii) Calcular el rendimiento neto del activo físico en el estado estacionario medido como
la productividad marginal del capital menos su tasa de depreciación. ¿De qué parámetros
depende?
12. (Septiembre 2004) En el modelo de Ramsey decimos que la trayectoria óptima
describe una “continua aproximación hacia el estado estacionario, pero sin llegar a entrar
en él”. Explicar por qué.
13. (Junio 2009) Una economía de Ramsey evoluciona por su trayectoria óptima y se
23
encuentra tan cerca del estado estacionario que, en la práctica, es como si estuviera en él.
El producto per capita en este estado estacionario es y = 2:0. La función de producción
es Cobb-Douglas con
= 0:5, la tasa de depreciación del capital es
= 0:20, la población
crece a una tasa constante del 1%, n = 0:01, y el parámetro de elasticidad de la función
de utilidad es
= 1:5.
i) Hallar el valor numérico de la tasa de preferencia intertemporal, , de esta economía.
ii) Obtener los niveles del capital per capita y el consumo per capita en el estado
estacionario. Representar el diagrama de fases y describir los elementos que aparecen en
él.
iii) Supongamos que los habitantes de esta economía se enteran de que en diez periodos
serán teletransportados a otro planeta donde las condiciones de vida sean mejores. Su
reacción es abandonar la zona del estado estacionario al transformar 0.25 unidades de
capital en consumo (es decir, se reduce en 0.25 el capital per capita para aumentar en
0.25 el consumo per capita). Utilizando las ecuaciones dinámicas del modelo, hallar las
variaciones esperadas para el capital per capita y el consumo per capita en el periodo
posterior. Representar la situación en el diagrama de fases y la nueva trayectoria óptima.
¿Cuál será el nivel del capital per capita en el momento de abandonar este planeta?
14. (Junio 2007) Una economía de Ramsey con mercados competitivos de trabajo,
capital y bonos, función de producción Cobb-Douglas, F (Kt ; Lt ) = Kt Lt1
de utilidad de elasticidad constante, U (ct ) =
c1t
1
1
, con horizonte temporal in…nito está
caracterizada por los siguientes valores de sus parámetros:
n = 0:02 y
, y función
= 0:40,
= 0:14,
= 0:06,
= 2:0.
i) Hallar los valores del capital per capita, y el consumo per capita del estado estacionario hacia el que se aproxima la única trayectoria óptima. Dibujar el diagrama de
fases de esta economía, y describir los elementos que aparecen en él.
ii) En el momento actual, el consumo per capita es c0 = 0:8 y el capital per capita
es k0 = 2:5. Hallar el consumo per capita y el capital per capita del siguiente periodo,
c1 y k1 . Representa la evolución de la economía en el diagrama de fases dibujado en
el apartado anterior. ¿Sospecharías que la dotación inical ya se encuentra en la única
trayectoria óptima?
iii) Calcular el salario, el tipo de interés del capital y el tipo de interés de los bonos
en el periodo 0. ¿Qué evolución esperarías para los tipos de interés a corto plazo y a qué
tasas se aproximan a largo plazo?
24
15. (Junio 2008) Una economía evoluciona de acuerdo al modelo de Ramsey con
mercados competitivos de trabajo, capital y bonos, función de utilidad con elasticidad
constante U (ct ) =
c1t
1
1
y función de producción Cobb-Douglas F (Kt ; Lt ) = Kt L1t
.
En un periodo inicial las cantidades de capital per capita y consumo per capita ya se
encuentran situadas sobre la única trayectoria óptima. Supongamos que entonces la tasa
de preferencia intertemporal de las familias se reduce desde su nivel inicial
bajo
0
a otro más
.
i) Representar el diagrama de fases y la trayectoria óptima con la tasa de preferencia
intertemporal inicial y con la nueva. Describir los elementos que aparecen en el grá…co.
ii) Valorar los efectos de la reducción de la tasa de preferencia intertemporal sobre
los niveles del capital per capita, consumo per capita y producto per capita en el estado
estacionario hacia el que se dirige la economía.
iii) Explicar el efecto que tiene este cambio sobre los tipos de interés a corto plazo y a
largo plazo, re…riéndose a los cambios que ocurrirán en los mercados de bonos y capitales.
El salario a largo plazo, ¿aumentará o disminuirá con el nuevo
0
< ?
16. (Septiembre 2008) i )Hallar el capital de la regla de oro en una economía con
función de producción Cobb-Douglas, tasa de crecimiento de la población constante y
exógena y tasa de depreciación del capital constante y exógena.
ii) A continuación, supongamos que en una economía de Ramsey, la familia se está
planteando cual es su tasa de preferencia intertemporal "deseada" y pretende …jar aquella
tasa que sitúe la única trayectoria óptima en una continua aproximación al capital de la
regla de oro. Conociendo que el capital se deprecia un 5% cada periodo, la población
crece al 3% cada periodo y
= 0:5 en la función de producción, hallar cual debería de
ser el valor numérico de la tasa de preferencia intertemporal para cumplir la regla de oro
y calcular el consumo per capita obtenido en ese estado estacionario.
iii) Representa como quedaría el diagrama de fases de esta economía. Describe los
elementos que aparecen en él.
17. (Junio 2009) Una economía de Ramsey con familias productoras, función de
producción Cobb-Douglas y función de utilidad isoelástica se encuentra dentro de la única
trayectoria óptima de aproximación al estado estacionario. Se conocen los siguientes datos
de esta economía: la tasa de depreciación del capital es
función de producción es
= 0:08, el coe…ciente
de la
= 0:40, el parámetro de elasticidad de la función de utilidad
25
es
= 1:8, la tasa de preferencia intertemporal es
= 0:04 y la población crece al 3%
por periodo; n = 0:03:
i) Escribir las ecuaciones dinámicas del modelo dados los valores numéricos de los
parámetros del modelo. Hallar los valores numéricos del capital per capita, el producto
per capita y el consumo per capita en el estado estacionario hacia el que se dirige la
economía.
ii) Supongamos que la tasa de crecimiento de la población se reduce al 2%, n =
0:02. Representar el diagrama de fases con la vieja y la nueva tasa de crecimiento de
la población, indicando los efectos que tendrá este cambio sobre la ubicación del estado
estacionario.
iii) Hallar las tasas de ahorro en estado estacionario con n = 0:03 y con n0 = 0:02.
¿Aumenta o disminuye la tasa de ahorro con la caída del crecimiento de la población?
18. (Mayo 2010) Una economía se comporta de acuerdo al modelo de Ramsey con
función de utilidad isoelástica, función de producción Cobb-Douglas y mercados competitivos de trabajo capital y bonos. La función de producción es Cobb-Douglas con
= 0:3,
el capital se deprecia un 8% cada periodo ( = 0:08), la tasa de preferencia intertemporal
= 0:04 y el crecimiento de la población es del 2% por periodo (n = 0:02). Finalmente,
el parámetro de la elasticidad de la función de utilidad tiene un valor
= 4:0.
i) Escribir las ecuaciones dinámicas que describen la evolución del capital per capita
y el consumo per capita en esta economía.
ii) Dibujar el diagrama de fases detallando los elementos que aparecen en él e incluyendo los valores numéricos del capital per capita y el consumo per capita en el estado
estacionario hacia el que se dirige la única trayectoria óptima.
iii) Supongamos que la tasa de depreciación del capital se reduce al 5%. Dibujar los
efectos sobre el diagrama de fases y calcular los nuevos niveles del capital per capita y el
consumo per capita en el estado estacionario hacia el que se dirige la única trayectoria
óptima.
iv) Calcular el tipo de interés del capital en el estado estacionario hacia el que se dirige
la única trayectoria óptima con ambas tasas de depreciación del capital. ¿Aumentan,
disminuyen ó permanecen igual al reducirse la tasa de depreciación?
19. (Mayo 2011) Se sabe que una economía de Ramsey con mercados competitivos se
encuentra muy, muy cerca del estado estacionario hacia el que se dirige la única trayectoria
26
óptima. Los parámetros estructurales que de…nen esta economía son
= 10,
= 0:35,
= 0:09,
= 0:03 y n = 0:01.
i) Dibujar el diagrama de fases, indicando los valores numéricos del estado estacionario
donde (casi) se situa la economía en el momento actual.
Supongamos que las familias se vuelven más impacientes a la hora de consumir y,
como consecuencia, sube la tasa de preferencia intertemporal a
0
= 0:05;
ii) Hallar los valores de capital per capita y consumo per capita en el nuevo estado
estacionario hacia el que se dirige la nueva trayectoria óptima e incluirlos en el diagrama
de fases.
iii) Calcular los valores iniciales y …nales del salario y el tipo de interés del capital.
Representar grá…camente la evolución que van a seguir estas dos variables a lo largo del
tiempo, desde el momento en el que aumenta la tasa de preferencia intertemporal hasta
que se aproximen al nuevo estado estacionario.
27
EJERCICIOS TEMA 4
Modelos de crecimiento endógeno. El modelo AK.
El modelo AK con tasa de ahorro constante.
1. En una economía con familias productoras, sin comportamiento optimizador y
con una tasa de ahorro constante s, la función de producción es Yt = AKt . El resto de
supuestos son los habituales: economía cerrada y sin sector público, tasa de crecimiento
de la población constante, tasa de depreciación del capital constante y la población es
igual a la mano de obra.
i) Obtener la ecuación fundamental y comentarla.
ii) Calcular las tasas de crecimiento de las variables per capita y de las variables
agregadas en el estado estacionario. Comentar los resultados.
iii) Representar grá…camente el estado estacionario obtenido (bajo todos los casos
posibles).
2. (Junio 2002) Existen dos economías cerradas y sin sector público, con la misma
tasa de ahorro constante, s = 0:22, con la misma tasa de crecimiento de la población,
n = 0:03, con la misma tasa de depreciación del capital,
= 0:15, y en ambas toda la
población trabaja. Su única diferencia está en la función de producción. En la primera
economía la función de producción es neoclásica del tipo Cobb-Douglas con progreso
tecnológico potenciador del trabajo Yt = F (At Lt ; Kt ) = Kt (At Lt )1
con
= 0:5 y con
:
tasa de crecimiento constante de la tecnología
At
At
= 0:02. En la segunda economía la
función de producción es AK, Yt = AKt , con A = 1:05. Se pide:
:
i) Hallar la tasa de crecimiento del producto per capita
y
=
y
y
en el estado estacionario
de las dos economías.
ii) En un momento inicial (periodo 0) la primera economía tiene un capital per capita
igual a k0 = 1:452 y un nivel tecnológico igual a A0 = 1:2. ¿Esta economía se encuentra
ya en el estado estacionario ó se está aproximando a él?
iii) En un momento inicial (periodo 0) la segunda economía también tiene un capital
per capita igual a k0 = 1:452. ¿Esta economía se encuentra ya en el estado estacionario
ó se está aproximando a él?
iv) Hallar el nivel del producto per capita en el periodo 10 en las dos economías.
3. (Septiembre 2004) Supongamos que existen dos economías cerradas y sin sector
público con la misma tasa de ahorro constante del 20% (s = 0:2), la misma tasa de
28
crecimiento de la población del 4% (n = 0:04) y la misma tasa de depreciación del capital
igual al 16% ( = 0:16). En estas dos economías toda la población trabaja y su única
diferencia radica en la tecnología de producción de la que disponen. En la primera de
ellas la función de producción es de coe…cientes …jos de Leontief Yt = min (AKt ; BLt ) con
A = 1:2 y B = 2:4 y en la segunda la función de producción es Yt = AKt siendo A = 1:2
también. En un momento inicial se sabe que el capital per capita en ambas economías es
k0 = 1.
:
i) Calcular la variación del capital per capita en este periodo k0 , su tasa de crecimiento
:
ko
=
k0
k0
y el capital per capita del periodo siguiente k1 para ambas economías.
:
ii) Calcular la tasa de crecimiento del producto per capita
y0
=
y0
y0
junto con el
producto per capita en el siguiente periodo y1 . ¿Coinciden para las dos economías?
iii) Hallar el estado estacionario de estas dos economías de…niendo las tasas de crecimiento de las variables per capita y de las variables agregadas.
iv) Comparar las dos economías. ¿En qué se parecen y en qué se diferencian?
4. (Junio 2005) Enumerar los factores que determinan la tasa de crecimiento a largo
plazo del producto per capita según el modelo AK con tasa de ahorro constante y exógena.
Poner ejemplos de políticas económicas que favorezcan el crecimiento económico según
estos resultados.
5. (Septiembre 2005) Se sabe que en dos economías la producción se obtiene a partir
de la función de producción Yt = 0:2Kt , la tasa de crecimiento de la población es constante
(n = 0:015), la tasa de depreciación del capital también es constante ( = 0:04), toda
la población trabaja y no hay sector público ni resto del mundo. Su única diferencia se
encuentra en el comportamiento seguido a la hora de decidir el consumo y el ahorro de
las familias. En la primera economía las familias tienen una tasa de ahorro constante y
exógena (s = 0:45), mientras que en la segunda tienen un comportamiento optimizador.
Maximizan la utilidad intertemporal con una función de utilidad U (ct ) =
c1t
1
1
con
= 4.
i) A partir de los supuestos del modelo AK con tasa de ahorro constante y exógena,
hallar la ecuación dinámica del capital per capita para la primera economía.
ii) Calcular la tasa de crecimiento del producto per capita en el estado estacionario
de la primera economía.
iii) En el momento actual, la tasa de crecimiento del capital per capita de las dos
29
economías es la misma. Sabiendo este dato, hallar la tasa de preferencia intertemporal
en la economía con comportamiento optimizador.
iv) ¿Cuántos periodos necesitarán estas economías para duplicar su producto per
capita? ¿Y para duplicar su producto agregado?
6. (Septiembre 2007) Una economía cerrada y sin sector público tiene una tasa de
ahorro constante en el 12% (s = 0:12), una tasa de depreciación del capital igual al 10%
( = 0:10), y disfruta de una teconología de producción AK. En el año 2005 la producción
total de esta economía era Y2005 = 12:60 millones de unidades y en el 2006 ascendió a
Y2006 = 13:23 millones de unidades.
i) Hallar la tasa de crecimiento del producto agregado de 2005 a 2006.
ii) Teniendo en cuenta el comportamiento del modelo AK, hallar la productividad
marginal del capital y el número de unidades de capital utilizadas en 2006.
iii) Si la población en 2006 es de 1 millón de habitantes y crece a una tasa constante
del 2%, determinar el valor del producto per capita de esta economía en 2025.
7. (Junio 2008) Existe una economía que consigue un crecimiento económico endógeno
al comportarse según predice el modelo AK con tasa de ahorro constante y exógena. La
productividad marginal del capital es A = 0:4, el capital se deprecia un 4% cada periodo
y la tasa de ahorro es del 15%.
i) Escribir la ecuación fundamental de este modelo y deducir la tasa de crecimiento de
la producción total (agregada). ¿De qué factores depende? ¿Cuál es su valor numérico?
ii) En el año 2007 el número de unidades totales producidas fue Y2007 = 38:52 millones.
Las autoridades económicas pretenden alcanzar una producción total de 70 millones de
unidades para el año 2025. ¿Crees que se conseguirá este objetivo? Si no es así, determina
cuánto tiene que cambiar la tasa de ahorro para que se llegue a ese objetivo. Cita alguna
medida de política económica que favorecería ese cambio.
8. (Septiembre 2009) Una economía crece de acuerdo al modelo AK con tasa de ahorro
constante en el 14% y tasa de depreciación del capital del 10%. La función de producción
es Yt = Kt .
Si en el año 2009 el PIB total es de 5 millones de unidades, hallar el PIB total en
2025.
9. (Mayo 2010) Tras un prolongado crecimiento, el producto per capita anual de
China ha pasado de 1350 dólares en 1990 a 4000 dólares esperados en 2010.
30
i) ¿Cuál ha sido su tasa anual de crecimiento medio en estos últimos 20 años?
ii) Supongamos que queremos explicar este crecimiento con el modelo AK con tasa
de ahorro constante del 25%, productividad marginal del capital igual a 0.6 y tasa de
depreciación del capital igual al 9%. ¿Cuál habrá sido el crecimiento medio anual de la
población en China en los últimos 20 años?
iii) Si el PIB per capita anual de EE.UU. en 2010 se situa en los 45000 dólares y se
espera que crezca al 1.5% en media durante este siglo. ¿Alcanzará China a EE.UU. en
términos de PIB per capita antes de que acabe el siglo XXI si es capaz de mantener el
ritmo de crecimiento de los últimos 20 años? En caso a…rmativo ¿en que año se igualarán
sus PIB per capita?
10. (Junio 2011) Una economía AK tiene una tasa de ahorro constante y exógena
(s = 0:18) y una tasa de depreciación del capital siempre del 6% anual ( = 0:06), y la
productividad marginal del capital es siempre A = 0:5. En el año 2000 la producción
per capita de esta economía era y2000 = 2 unidades y en el 2010 ascendió a y2010 = 2:255
unidades.
i) Utilizando el concepto de tasa de crecimiento instantánea, hallar la tasa de crecimiento anual del producto per capita entre los años 2000 y 2010.
ii) Hallar la tasa de crecimiento de la población.
iii) Si la población en 2010 es de 40 millones de habitantes, calcular el ahorro agregado
de esta economía en 2040.
El modelo AK con comportamiento optimizador.
10. Una economía con familias productoras optimizadoras, tiene una función de producción Yt = AKt . La función de utilidad de las familias es de elasticidad constante
U (ct ) =
c1t
1
1
.
i) Plantear y resolver el problema de optimización de las familias en un horizonte
temporal in…nito. Hallar las ecuaciones dinámicas del consumo y el capital per capita.
ii) Calcular las tasas de crecimiento de las variables per capita y las variables agregadas
en el estado estacionario. ¿De que depende el crecimiento económico en este modelo?
11. Una economía con agentes optimizadores y mercados competitivos de capital y
bonos tiene una función de producción Yt = AKt . La función de utilidad de las familias
es de elasticidad constante U (ct ) =
c1t
1
1
.
31
i) Utilizando el criterio del máximo bene…cio, hallar la ecuación de la demanda de
capital de la empresa representativa. Comentarla.
ii) Utilizando el criterio de la máxima utilidad con un horizonte temporal in…nito,
hallar la ecuación dinámica del consumo de la familia representativa.
iii) Calcular las tasas de crecimiento de las variables per capita y las variables agregadas en el estado estacionario. Comparar los resultados obtenidos con los del ejercicio
anterior.
iv) ¿A qué tasa crecerá el tipo de interés en el estado estacionario?
12. ¿Cómo afectaría a la tasa de crecimiento del consumo per capita obtenida en el
problema anterior?
i) Un aumento de la productividad marginal del capital A.
ii) Un aumento de la tasa de depreciación del capital .
iii) Un aumento de la tasa de crecimiento de la población n.
iv) Un aumento de la tasa de preferencia intertemporal .
v) Un aumento de la elasticidad de la utilidad marginal del consumo con respecto del
nivel de consumo, .
vi) Un aumento del tipo de interés de los bonos, r.
13. (Septiembre 2002) A partir de las ecuaciones dinámicas y las tasas de crecimiento,
se pide demostrar que en el modelo AK con comportamiento optimizador, función de
utilidad con elasticidad constante U (ct ) =
c1t
1
1
y mercados competitivos de capital y
bonos:
i) El producto per capita crece, o al menos puede llegar a crecer, a una tasa positiva
en el largo plazo (primer hecho estilizado de Kaldor).
ii) El ratio capital agregado entre producto agregado,
K
,
Y
se mantiene constante en el
largo plazo (segundo hecho estilizado de Kaldor).
iii) El coste de uso del capital, la productividad marginal del capital y el tipo de
interés de los bonos se mantienen constantes en el largo plazo (tercer hecho estilizado de
Kaldor).
Nota: Considera que la economía se encuentra en el largo plazo una vez alcanzado el
estado estacionario.
14. (Septiembre 2003) Una economía evoluciona de acuerdo al modelo AK con comportamiento optimizador, horizonte temporal in…nito, y mercados competitivos de capital
32
y bonos. La productividad marginal del capital es A = 0:16 y su tasa de depreciación
es
= 0:10. Las función de utilidad de las familias es U (ct ) =
tasa de preferencia intertemporal es
c1t
1
1
con
= 4 y su
= 0:02: La población crece un 1.5% por periodo
(n = 0:015).
i) Teniendo en cuenta tanto el comportamiento maximizador de bene…cios de la empresa competitiva como la condición de arbitraje, hallar el valor numérico del tipo de
interés de los bonos.
ii) Plantear el problema de optimización de las familias consumidoras y obtener la
ecuación dinámica del consumo per capita.
iii) Calcular el valor numérico de la tasa de crecimiento instantánea del consumo per
capita en el estado estacionario,
c.
iv) En el momento actual el consumo per capita es c0 = 2:6. Hallar el consumo per
capita dentro de 4 periodos, c4 .
15. (Junio 2004) Comparación entre crecimiento exógeno y crecimiento endógeno.
Economía A: Representada por el modelo de Solow-Swan con progreso tecnológico
potenciador del trabajo recogido en una función de producción Cobb-Douglas Yt =
Kt (At Lt )1
con
= 0:5. Además la tasa de ahorro es del 15% (s = 0:15), la tasa
de depreciación del capital es el 8% por periodo ( = 0:08), la tasa de crecimiento de la
población es del 2% por periodo (n = 0:02), y la tasa de crecimiento de la tecnología es
también del 2% por periodo (x = 0:02).
Economía B: Representada por el modelo AK con comportamiento optimizador y
familias productoras. La productividad marginal del capital es A = 0:25 y la tasa de
depreciación del capital es, al igual que en la economía A, del 8% por periodo ( = 0:08).
Las familias tienen una función de utilidad con elasticidad constante
= 3 y la tasa de
preferencia intertemporal es del 2% por periodo ( = 0:02).
i) Calcular la tasa de crecimiento del producto per capita en el estado estacionario de
las dos economías.
ii) Se conoce que en el momento actual la economía A se encuentra ya en el estado
estacionario con un producto per capita y0 = 2:5. Calcular el valor de la variable tecnológica en el momento actual, A0 .
iii) La economía B en el momento actual tiene un producto per capita de y0 = 2
unidades, inferior por tanto al de la economía A. ¿Llegará un momento futuro en el que
el producto per capita de la economía B supere al de la economía A? Si es así, ¿a partir de
33
que periodo será? Representar en un mismo grá…co la evolución del producto per capita
de las dos economías a lo largo del tiempo.
16. (Junio 2009) Dos economías crecen de acuerdo al modelo AK y tienen la misma
productividad y el mismo crecimiento de la población. En una de ellas la tasa de ahorro
es constante en el 30% (s = 0:30) mientras que en la otra las decisiones de consumo y
ahorro se toman resolviendo un problema de maximización de la utilidad con una función
de utilidad isoelástica con
= 6:0.
i) Escribir las ecuaciones dinámicas y obtener a partir de ellas la tasa de crecimiento
del PIB per capita en función de los parámetros del modelo.
ii) Se conoce que la tasa de crecimiento del PIB per capita es del 2% en ambas
economías. También se sabe que la tasa de depreciación del capital es del 3% en ambos
casos y la tasa de preferencia intertemporal es
= 0:04 en la segunda economía. Hallar
la productividad marginal del capital y la tasa de crecimiento de la población.
iii) Si en el momento actual, el PIB per capita es igual a 2 en la economía con tasa
de ahorro constante, mientras que es igual a 2:5 en la economía con comportamiento
optimizador. ¿Cuál será el valor del PIB per capita dentro de 50 periodos para cada una
de estas dos economías?¿Se habrá producido una convergencia económica entre ellas?¿Por
qué?
34
EJERCICIOS TEMA 5.
La evidencia empírica.
1.- Beta convergencia y sigma convergencia entre los países de la UE con anteriodad
a la ampliación de 2004 durante el periodo 1967-1992.
En la Tabla 1 del material complementario a este tema se encuentran disponibles los
datos de la renta (producto) per capita real de estos 15 países de la UE durante el periodo
1967-1992. Deseamos conocer si entre estos países se ha producido o no un proceso de
convergencia económica en estos 25 años. Para ello necesitamos determinar la presencia
o ausencia de -convergencia y -convergencia.
i) Calcular el valor del estimador de
i
donde
i
=
en la regresión por mínimos cuadrados
log(yi;1967 ) + ui ;
es la tasa de crecimiento anual media del producto per capita del país i,
log(yi;1967 ) es el logaritmo del producto per capita del país i en el periodo inicial (año
1967) y ui es un componente aleatorio de error.
ii) Representar grá…camente la nube de puntos ( i ; log(yi;1967 )) y la recta de regresión.
iii) Discutir la existencia de -convergencia.
iv) Calcular el valor de la varianza del logaritmo del producto per capita de los 15
países para cada año t 2 [1967; 1992]
P15
2
n=1 (log(yn;t )
t =
15
v) Representar grá…camente la desviación estándar
log(y t ))2
t
a lo largo del periodo [1967; 1992] :
Comprobar la existencia o no de -convergencia.
Nota: Los resultados de este ejercicio se proporcionan directamente al alumno dentro
del material complemetario al tema 5.
2. (Junio 2003) La siguiente tabla recoge datos de crecimiento económico en 12
países del mundo durante el periodo 1980-1997, y ha sido obtenida del Informe sobre el
Desarrollo Mundial del Banco Mundial. La columna A representa la tasas de crecimiento
medias
i
en el periodo 1980-1997 y la columna B representa el logaritmo del producto
per cápita en el año 1980 log(yi;1980 ) para estos países. Las medias de las columnas A y
B son, respectivamente, A = 0:0133 y B = 7:5492.
35
A
A
B
B
A
A
B
B
B
B
A
B
Australia
0.023
9.27
0.0097
1.7208
0.0168
2.9613
Brasil
0.012
7.57 -0.0013
0.0208
-0.0001
0.0004
Etiopía
0.007
4.91 -0.0063 -2.6392
0.0165
6.9652
EEUU
0.017
9.39
0.0037
1.8408
0.0069
3.3887
Francia
0.013
9.41 -0.0003
1.8608
-0.0005
3.4627
Honduras
0.005
6.46 -0.0083 -1.0892
0.0090
1.1863
India
0.041
5.52
0.0277
-2.0292
-0.0563
4.1175
Italia
0.014
8.99
0.0007
1.4408
0.0011
2.0760
Japón
0.021
9.11
0.0077
1.5608
0.0121
2.4362
Kenya
0.004
6.06 -0.0093 -1.4892
0.0138
2.2176
Nigeria
-0.008 6.80 -0.0213 -0.7492
0.0159
0.5613
Perú
0.010
0.0015
0.2018
7.10 -0.0033 -0.4492
i) Calcular el valor del estimador de
i
=
2
en la regresión por mínimos cuadrados
log(yi;1980 ) + ui ;
donde ui es un componente aleatorio de error.
ii) Representar grá…camente la nube de puntos ( i ; log(yi;1980 )) y la recta de regresión.
Comenta brevemente la in‡uencia a la convergencia mundial que provocan India y Etiopía.
iii) Atendiendo al resultado del apartado anterior, discutir la existencia de -convergencia
entre estos 12 países de la economía mundial durante el periodo 1980-1997. El resultado
obtenido, ¿apoyaría la utilización de modelos con crecimiento endógeno o exógeno para
estudiar el crecimiento económico mundial? Pon un ejemplo de un modelo que quedaría
validado por el resultado empírico obtenido. Razona tus respuestas.
3. Hechos estilizados de Kaldor y modelos de crecimiento económico.
Analizar el cumplimiento de los tres primeros hechos estilizados de Kaldor en los
siguientes modelos:
i) Modelo de Solow-Swan con progreso tecnológico potenciador del trabajo y función
de producción Cobb-Douglas.
ii) Modelo de Ramsey con función de producción Cobb-Douglas y mercados competitivos de trabajo, capital y bonos.
iii) Modelo AK con tasa de ahorro constante y exógena.
36
4. (Junio 2002) Comentar el siguiente texto: ”el supuesto de rendimientos marginales
decrecientes del capital per capita llevan a los modelos de crecimiento exógeno a predecir
la convergencia entre naciones. Por el contrario, los rendimientos constantes del capital
subyacentes en todos los modelos de crecimiento endógeno comportan la predicción de
no convergencia entre países pobres y países ricos”.
5. (Junio 2004) El siguiente grá…co representa la evolución de la varianza del logaritmo
del producto per capita entre un conjunto muy diverso de 60 países de la economía mundial
durante el periodo 1980-2000. Comentar las implicaciones del resultado observado en
relación a:
i) el analísis empírico de la convergencia económica mundial.
ii) la validación de resultados que predicen los modelos de crecimiento económico.
1
0.95
Varianza(log(y))
0.9
0.85
0.8
0.75
0.7
0.65
0.6
1980
1982
1984
1986
1988
1990
Año
1992
1994
1996
1998
2000
6.- (Septiembre 2004) -convergencia en la comarca de Pamplona. La siguiente tabla
presenta datos aproximados sobre el producto per capita en 1984 (y1984 ), el logaritmo del
producto per capita en 1984 (log(y1984 )), el producto per capita en 2004 (y2004 ), y la tasa
de crecimiento media del producto per capita en los últimos 20 años ( y ), es decir de
1984 a 2004, obtenidos para 10 localidades de la comarca de Pamplona. El producto per
capita aparece expresado en euros constantes.
37
Localidad
y1984
log(y1984 )
y2004
y
Barañáin (BA) 14100
9.55
19000 1.50
Berriozar (BE)
9600
9.17
16900 2.87
Burlada (BU)
12200
9.41
18900 2.21
Huarte (H)
11500
9.35
19800 2.75
Mutilva (M)
13100
9.48
21100
Noáin (N)
10700
9.28
18500 2.78
Orcoien (O)
10500
9.26
20200 3.33
Pamplona (P)
14900
9.61
20600 1.63
Villava (V)
12600
9.44
18700 1.99
Zizur (Z)
16200
9.69
22000 1.54
i) Sabiendo que la tasa de crecimiento media (expresada en %) se ha calculado como
la tasa de crecimiento anual acumulada a lo largo del periodo 1984-2004, se pide rellenar
el hueco que falta en la tabla (
y
para Mutilva).
ii) Representar la nube de puntos que utilizaríamos para el análisis grá…co de la convergencia. Se recomienda escribir las iniciales de cada localidad junto a su posición
en la nube de puntos. Comentar las posiciones que ocupan Berriozar (BE) y Zizur (Z).
iii) Esbozar la recta de regresión (sin calcularla exactamente) que aproximaría mejor
la relación que se aprecia en la nube de puntos. ¿Crees que ha existido -convergencia
entre las economías de la comarca de Pamplona durante los últimos 20 años?
iv) Relacionar brevemente el resultado anterior con los modelos de Crecimiento Económico.
7. (Junio 2005) Efecto euro y convergencia económica.
La siguiente tabla informa sobre el producto per capita en Alemania y España en los
años 1999 y 2004 en euros constantes del año 2000:
Alemania
España
y1999
24396 e
16259 e
y2004
25517 e
18579 e
i) Calcular la tasa de crecimiento anual acumulada del producto per capita en Alemania y España en los cinco primeros años de la moneda única (1999-2004).
ii) ¿Crees que se ha producido una convergencia económica en sentido
entre Ale-
mania y España durante este periodo de introducción del euro? Razonar la respuesta.
38
8. (Junio 2007) ¿ -convergencia entre las Comunidades Autónomas?. La siguiente
tabla recoge datos, en la columna A, sobre la tasa de crecimiento anual media del producto per capita de cada una de las 17 Comunidades Autónomas durante el perido 19862006 ( i ) y, en la columna B, aparece el logaritmo de su producto per capita en 1986
(log(yi;1986 )). Las medias aritméticas de los datos pertenecientes a las columnas A y B
son A = 2:75 y B = 9:26.
A
i; %
B
log(yi;1986 )
Andalucía (AN)
3.38
9.02
Aragón (AR)
2.26
9.32
Asturias (AS)
1.56
9.18
Baleares (BA)
2.78
9.39
Canarias (CANA)
3.03
9.19
Cantabria (CANT)
2.90
9.28
Castilla La Mancha (CLM)
2.49
9.05
Castilla León (CLE)
1.89
9.25
Cataluña (CAT)
2.44
9.46
Com. Valenciana (VA)
3.50
9.26
Extremadura (EX)
2.99
8.84
Galicia (GA)
2.14
9.10
La Rioja (LR)
2.53
9.33
Madrid (MA)
3.01
9.56
Murcia (MU)
3.72
9.11
Navarra (NA)
3.37
9.54
País Vasco (PV)
2.79
9.55
i) Utilizando las casillas dispuestas en la tabla anterior para los cálculos numéricos
requeridos, hallar el valor del estimador de
i
=
en la regresión por mínimos cuadrados
log(yi;1986 ) + ui ;
donde ui es un componente aleatorio de error.
ii) Representar la nube de puntos y la recta de regresión para el análisis grá…co de
la -convergencia (emplear las iniciales de cada Comunidad Autónoma para indicar su
posición en la nube de puntos y acotar los ejes de acuerdo a los valores de las columnas A
39
y B). Comentar las posiciones que ocupan Andalucía (AN) y Navarra (NA) en el grá…co y
de qué signo es su aporte a la covarianza. ¿Crees que ha existido convergencia en sentido
entre las economías de las Comunidades Autónomas durante el periodo 1986-2006?
iii) Teniendo en cuenta que las Comunidades Autónomas comparten una estructura
económica con características similares, relacionar brevemente el resultado anterior con
los modelos de Crecimiento Económico.
9. (Septiembre 2009) La siguiente tabla recoge datos, en la columna A, sobre la tasa
de crecimiento anual acumulada del producto per capita de nueve países de América del
Sur en los últimos 25 años, 1983-2008 ( i ) y, en la columna B, aparece el logaritmo de
su producto per capita en 1983 (log(yi;1983 )).
A
i; %
B
log(yi;1983 )
Argentina (ARG)
0.58
9.05
Bolivia (BOL)
-0.45
8.19
Brasil (BRA)
2.95
8.53
Colombia (COL)
1.17
8.38
Chile (CHI)
3.78
9.02
Ecuador (ECU)
0.25
8.32
Perú (PER)
1.45
8.41
Uruguay (URU)
2.65
8.91
Venezuela (VEN)
1.85
9.09
i) Representar la nube de puntos y esbozar la recta de regresión para el análisis grá…co
de la -convergencia. Comentar los resultados.
ii) Utilizando las casillas dispuestas en la tabla anterior para los cálculos numéricos
requeridos, hallar el valor del estimador de
i
=
en la regresión por mínimos cuadrados
log(yi;1983 ) + ui ;
donde ui es un componente aleatorio de error.
iii) ¿Qué países han sido los que más han favorecido la convergencia económica en
América del Sur?¿Y cuáles han sido los que más han favorecido la divergencia económica?
Razona tus respuestas.
10. Contabilidad del Crecimiento y Residuo de Solow.
40
La economía de Cobbiland es capaz de producir de acuerdo a una función de producción neoclásica tipo Cobb-Douglas con progreso tecnológico potenciador del trabajo,
Yt = Kt (At Lt )1
. Se ha estimado el valor numérico del coe…ciente
y se ha obtenido
= 0:36. La siguiente tabla recoge los datos de producción per capita y capital per capita
anuales durante el periodo 1993-2007
Año
yt
kt
1993 40.0 12.1
1994 40.8 12.2
1995 41.7 12.6
1996 42.6 12.9
1997 43.5 12.8
1998 44.1 13.1
1999 44.3 13.2
2000 45.8 13.8
2001 46.6 14.1
2002 46.6 14.4
2003 47.0 14.7
2004 48.2 14.5
2005 49.9 14.8
2006 51.6 15.0
2007 52.3 15.3
i) Hallar la serie de residuos de Solow en logaritmos, log(At ).
ii) Hallar las tasas de crecimiento de los residuos de Solow a partir de la serie anterior.
iii) Comprobar si para el caso de Cobbiland se cumple la hipótesis de los determinantes
del crecimiento a largo plazo en los modelos de crecimiento exógenos.
11. (Septiembre 2008) El producto agregado, capital agregado y número de trabajadores de una economía han evolucionado desde 1980 a 2007 tal y como recoje la siguiente
tabla
Producción
Capital
Y1980 = 12500 K1980 = 4300
Trabajo
L1980 = 9350
Y2007 = 22800 K2007 = 7650 L2007 = 12230
41
i) Hallar la tasa de crecimiento anual acumulada del producto agregado y del número
de trabajadores durante el periodo 1980-2007.
ii) Se conoce que la producción agregada de esta economía se obtiene de acuerdo a
una tecnología Cobb-Douglas con progreso tecnológico incorporado, Yt = Kt (At Lt )1
con
= 0:36. Hallar el residuo de Solow en 1980 y 2007.
iii) Suponiendo que la población crece a la misma tasa que la mano de obra (hallada
en el apartado i), valorar el cumplimiento del resultado obtenido en el modelo SolowSwan con progreso tecnológico incorporado acerca de los determinantes del crecimiento
económico a largo plazo.
12. (Junio 2010) La siguiente Tabla, extraída de Wikipedia, recoge el producto per
capita anual de los países del G7 en 2010 y la proyección para 2025 (medidos en dólares
constantes de EE.UU. en 2010):
País
EE.UU.
y2010
y2025
$47014 $57446
Reino Unido $41543 $52220
Canadá
$40541 $48621
Francia
$38380 $48429
Alemania
$37474 $45033
Japón
$36194 $46419
Italia
$31123 $41358
i) Para cada país, calcular la tasa de crecimiento anual acumulada esperada para los
próximos 15 años.
ii) Dibujar la nube de puntos correspondiente para el análisis de la -convergencia y,
esbozando la recta de regresión, discutir la posible existencia de convergencia entre los
países del G7 para los próximos años.
13. (Mayo 2011) La siguiente tabla recoge datos de PIB per capita real en 1999 y
2008 en 6 regiones pertenecientes a la Unión Europea
42
log(yi;1999 )
y1999
y2008
Aquitaine (A)
18100e
25300e
9.80
Bruxelles (B)
42200e
53100e
10.65
Hamburg (H)
36800e
47100e
10.51
Madrid (M)
23200e
33500e
10.05
Peloponnisos (P) 14200e
21100e
9.56
i
Tirol (T)
23600e 30900e
10.07
i) Calcular la tasa de crecimiento anual acumulada para cada región durante el periodo
1999-2008 y rellenar con los resultados la columna
ii) Calcular el valor del estimador de
i
=
i:
en la regresión por mínimos cuadrados
log(yi;1999 );
donde ui es un componente aleatorio de error.
iii) Representar grá…camente la nube de puntos ( i ; log(yi;1999 )) y la recta de regresión.
Destacar alguna región que muestre una contribución signi…cativa a la convergencia.
Discutir la posible existencia de convergencia económica.
43