1 Trabajo realizado por una fuerza variable

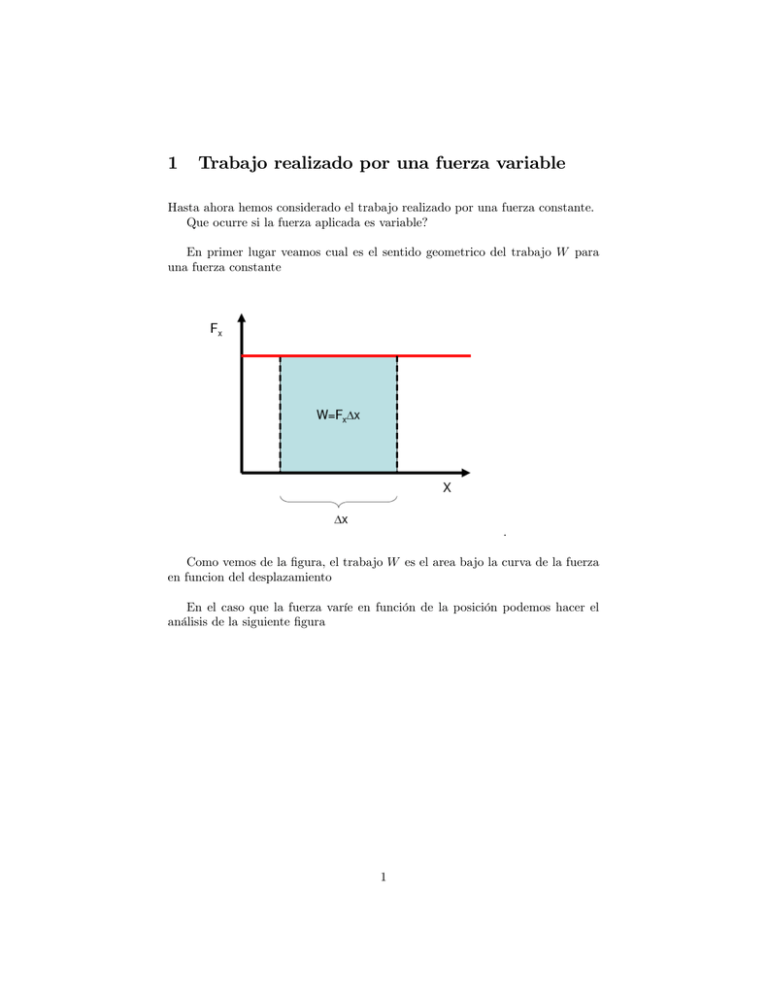
1
Trabajo realizado por una fuerza variable
Hasta ahora hemos considerado el trabajo realizado por una fuerza constante.
Que ocurre si la fuerza aplicada es variable?
En primer lugar veamos cual es el sentido geometrico del trabajo W para
una fuerza constante
.
Como vemos de la …gura, el trabajo W es el area bajo la curva de la fuerza
en funcion del desplazamiento
En el caso que la fuerza varíe en función de la posición podemos hacer el
análisis de la siguiente …gura
1
Dividimos el eje de las x en intervalos x contiguos y, para cada uno de
ellos, aproximamos el valor del área debajo de la curva, que describe a la fuerza
en esa región, por el área del rectángulo asociado a una fuerza constante en x
(el valor de esta fuerza constante podría ser el promedio del los valores en los
extremos del intervalo F x = 12 (F (x) + F (x + x)) )
De este modo, el trabajo W puede ser aproximado por la suma de trabajos
de fuerzas constantes en cada intervalo.
X i
W
Fx x
i
P
( denota la suma)
Cuanto mas pequeños sean los intervalos
entonces
W = lim
x!0
X
x mejor será la aproximación,
i
Fx x
i
De este modo, para un caso de fuerzas cuya dependencia con x sea sencilla
como en el caso de la siguiente …gura, tenemos
2
Tenemos
Para el intervalo que va desde x = 0 a x = x1 ; con
x1 = x1
W1 = Fx x1
Para el intervalo que va desde x = x1 a x = x2 (sera el area
del triángulo) con x2 = x2 x1
W2 =
1
Fx x2
2
El trabajo total será entonces
W = W1 + W2
Ejercicios
1) La fuerza ejecida por un resorte cuya longitud varía en l (medido respecto de la longitud del resorte cuando sobre él no se ejerce ninguna fuerza)
es
F = k l
y se ejerce en la dirección del resorte.
3
k se llama la constante del resorte y determina cuán "duro" es el mismo
N
Sea k = 400 m
Sea la masa del bloque = 4kg
El resorte se encuentra inicialmente comprimido en la posición x1 = 5cm
respecto del su posición de equilíbrio,
Calcular:
a) El trabajo realizado por el resorte cuando el bloque se desplaza desde
x1 = 5cm a x2 = 0
b) La velocidad del bloque en x2 = 0
2) Calcular la velocidad del bloque cuando alcanza una distancia de 3cm; si
parte de x = 0 con una velocidad de 0; 5m=s
2
Producto escalar
Cuando estudiamos el trabajo realizado por una fuerza, en el caso de un cuerpo
que se desplazaba según x; vimos que
W = F x cos( ) = Fx x
Es decir, calculamos el producto de la componente de la fuerza en la dirección
del movimiento y lo multiplicamos por la distancia recorrida.
4
Este producto (que involucra dos vectores, la fuerza y el desplazamiento) se
denomina "producto escalar". Se denota del siguiente modo:
! !
A B = AB cos
Donde
es el ángulo entre los dos vectores
Propiedades del producto escalar
! !
! !
Si A y B son perpendiculares =) A B = 0
! !
! !
Si A y B son paralelos =) A B = AB
! !
Si A B = 0 =) son paralelos o A = 0 o B = 0
! !
A A = A2
! ! ! !
A B =B A
! ! ! ! ! ! !
A+B
C = A C +B C
Si representamos los vectores por sus componentes
!
A = Ax x
b + Ay yb
donde x
b y yb se llaman versores y son vectores unitarios (de "longitud" 1) y
en la dirección de los ejes x e y. Su sentido es en general el de las x positivas y
las y positivas.
Dada esta notación el producto escalar de dos vectores es
! !
A B = (Ax x
b + Ay yb) (Bx x
b + By yb) = (Ax Bx ) x
b + (Ay By ) yb
Ejercicios
1)
!
!
Dado un vector A = (3b
x + 2b
y ) y otro B = (4b
x
i) El ángulo que forman
!
!
ii) La componente de A en la dirección de B
2)
5
3b
y ) ; calcular :
Sea un bloque sobre un pendiente como se muestra en la …gura anterior
Sobre el bloque actúa una fuerza:
!
F = 100N x
b + 0 yb
Calcular el trabajo de la fuerza cuando el bloque se desplaza desde el origen
hasta la posición que se muestra en la …gura.
6