Diapositivas Probabilidad (sesion 2)

VARIABLES ALEATORIAS
Definición: Se define como Variable Aleatoria a una representación
numérica de los resultados de un experimento aleatorio
X
Variable
Aleatoria
0
S
1
2
Espacio Muestral
3
4
Ejemplo: se verifican tres componentes para valorar su estado de funcionamiento
S = [ NNN, NND, NDN, NDD, DNN, DND, DDN, DDD]
Sea X= 0, 1, 2 ,3 :
Número de unidades defectuosas encontradas
X es una Variable Aleatoria
VARIABLES ALEATORIAS
Ejemplo: Se sacan dos pelotas consecutivamente, de una urna, que contiene 4
pelotas rojas y 3 blancas. Defina la variable aleatoria Y: Numero de pelotas rojas
extraídas
Espacio Muestral (S)
Y
RR
2
RB
1
BR
1
BB
0
Ejercicio 1: Un embarque de 5 automóviles extranjeros incluyen 2 que tiene unas
ligeras manchas de pintura. Si una agencia recibe 3 de estos vehículos. Defina la
variable aleatoria X: Número de vehículos manchados que recibió la empresa, y
determine su función de probabilidad.
Ejercicio 2: Se escogen 5 bombillas de un lote de producción y se desea evaluar
su tiempo de duración. Describa la variable aleatoria asociada a este experimento
aleatorio
VARIABLES ALEATORIAS
Definiciones:
1. Se dice que una variable aleatoria X es Discreta si el número de
valores que puede obtener es contable (ya sea finito o infinito), dicho
de otra manera si éstos pueden arreglarse en una secuencia que
corresponde con los enteros positivos
2. Se dice que una variable aleatoria X es Continua si su resultado
puede tomar cualquier valor dentro de la recta numérica
Ejercicio: Clasifique las siguientes variables aleatorias como discretas o continuas
X: Número de accidentes en la ciudad de Cali en el año 2007
Y: Tiempo que se demora un partido de Béisbol
M: Cantidad de leche producida por una vaca
N: Numero de huevos que pone una gallina en un mes
Funciones de Probabilidad
Definición:
Se define como una función de probabilidad, a una función que asocia
una probabilidad de ocurrencia a cada uno de los valores que asume
una variable aleatoria. La cual se denota como:
X Discreta
X Continua
p (x ) = P ( X = x )
P( X = x) = 0
∀x
f (x ) : función de densidad
Ejemplo: Se sacan dos pelotas consecutivamente de una urna, que contiene 4
pelotas rojas y 3 blancas. Defina la variable aleatoria Y: Número de pelotas rojas
extraídas, y halle su función de probabilidad
Funciones de Probabilidad
La función de probabilidad de una variable aleatoria discreta, debe satisfacer las
siguientes condiciones:
1.
2.
3.
p (x ) ≥ 0
para todos los valores x de X
p ( x ) ≤ 1 para todos los valores x de X
∑ p (x ) = 1
x
Ejemplo:
X
0
1
3
P(X=x)
1/3
1/2
1/6
Distribución de Probabilidad Acumulativa
Se define como la función que cuantifica la probabilidad de que la variable
aleatoria X asuma un valor menor o igual a x:
F (x ) = P ( X ≤ x ) =
∑ p (x )
xi ≤ x
i
Esta función de distribución cumple con las siguientes propiedades:
1. 0 ≤ F (x ) ≤ 1
para cualquier x
2 . F ( xi ) ≥ F (x j ) si xi ≥ x j
3. P ( X > x ) = 1 − F (x )
4 . P ( X = x ) = F ( x ) − F ( x − 1)
5.
P (xi ≤ X ≤ x j ) = F (x j ) − F ( xi − 1)
Ejercicio
La distribución de probabilidad de X, el numero de defectos por cada 10 metros
de una tela sintética en rollos continuos de ancho uniforme; es:
X
0
1
2
3
4
P (X)
0.41
0.37
0.16
0.05
0.01
a) Verifique que esta es una función de probabilidad.
b) Halle la función de distribución acumulada.
c) Evalué las siguientes probabilidades a través de la función de distribución.
P(X ≤ 3)
P(X>2)
P(1≤ X ≤ 3)
d) Grafique la Función de Distribución Acumulada.
P(X=1)
Función de Densidad
(Variable Continua)
Se dice que f(x) es la función de densidad de una variable aleatoria X del tipo
continuo, si:
1 . f (x ) ≥ 0,
−∞ < x < ∞
∞
2.
∫ f (x )dx = 1
−∞
3 . P (a < x < b ) =
b
∫ f (x )dx
a
Por definición una variable aleatoria continua tiene una probabilidad cero de
asumir un valor especifico:
P (X = a) =0 si X es continua
Función de Densidad (Variable Continua)
Ejemplo 1: Suponga que el error en la temperatura de reacción, en °C, par a un
experimento controlado de laboratorio es una variable aleatoria continua X,
que tiene como función de densidad a:
X2/3
-1<X<2
f(x) =
o en otro caso
a) Verifique que f(x) es efectivamente una función de densidad.
b) Evalué P(0<X<1)
Ejemplo 2: Si la utilidad por automóvil de un distribuidor, en unidades de mil, tiene
como función de densidad a:
f ( x ) = k (1 − x )
0 < X <1
a) Determine el valor de K que permite a esta función ser una función de
distribución valida
Función de Distribución Acumulada
(Variable Continua)
La función de probabilidad acumulativa de una variable aleatoria continua está
dada por
F (x ) = P ( X < x ) = P ( X ≤ x ) =
x
∫ f (x )dx
−∞
Algunas consideraciones sobre la distribución de
probabilidad Acumulada
1.
F (− ∞ ) = 0
3.
2.
F (∞ ) = 1
4.
P (a < X < b ) = F (b ) − F (a )
∂F (x )
= f (x )
∂x
Función de Distribución (Variable Continua)
Ejemplo 2: Si la utilidad por automóvil de un distribuidor, en unidades de mil, tiene
como función de densidad a:
f ( x ) = 2 (1 − x )
0 < X <1
Determine la función de distribución acumulada F(X)
Evalué P(X<0.5), P(0.5 < X <0.75)
Evalué P(X>0.6)
Ejemplo 3: La función de distribución acumulada de una variable aleatoria esta
dada por
 0
 2x + x2
F (x ) = 
 3
 1
Determinar la función de densidad de X.
Calcular P(X<1/2) y P(X>3/4).
x<0
0 < x <1
x >1
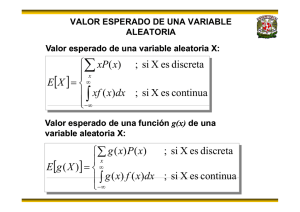
VALOR ESPERADO O ESPERANZA
Se denomina valor esperado de una variable aleatoria a su valor medio o
promedio poblacional, calculado a través de su función de probabilidad
P(X), en el caso discreto, o de densidad f(x) en el caso continuo
E ( X ) = ∑ xp ( x )
E (X ) =
si x es discreta
∞x
(
)
xf
x
dx
∫
si x es continua
−∞
Algunas propiedades del valor esperado:
E (c ) = c
E (ax ) = aE ( x )
E (ax + b ) = aE ( x ) + b
En general es posible calcular el valor esperado de
cualquier función de X
E ( g ( X )) = ∑ g ( x ) p ( x )
E ( g ( X )) =
si x es discreta
∞x
∫ g (x ) f (x )dx
−∞
si x es continua
VARIANZA
Cuantifica la magnitud de la variabilidad de una variable aleatoria, de manera
que un valor pequeño de este indicador sugiere homogeneidad, mientras que
por el contrario un valor grande indica dispersión
 ∑ ( x − E [ X ]) 2 * p ( x )
 X
2
Var ( X ) = E ( X − E [ X ]) =  ∞
 ∫ ( x − E [ X ]) 2 * f ( x ) dx
 − ∞
[
]
( )
Var ( X ) = E X 2 − E ( X )
2
Algunas propiedades de la Varianza:
Var (c ) = 0
Var (ax ) = a 2Var ( x )
Var (ax + b ) = a Var ( x ) + b
2
EJEMPLO
1. Determine el valor esperado y la varianza de cada una de las siguientes
funciones de probabilidad
X
0
1
2
3
4
P (X)
0.2
0.1
0.3
0.3
0.1
2. Calcule el valor Esperado y la Varianza de Y = 3X+4
2
x
f ( x) =
3
−1 < x < 2
Ejercicio
La demanda diaria en toneladas para un determinado producto alimenticio que se
vende a granel es una variable aleatoria X con función de densidad
f ( x ) = kx (1 − x )
4 < X < 10
a)
Determine el valor adecuado de la constante k para que f(x) pueda ser
considerada como una función de densidad.
b)
Cual es la demanda promedio por día y cual su varianza?
c)
Si se desea un nivel de servicio superior al 90% cual es la cantidad de
toneladas de productos mínima de la que debe disponerse en el inventario al
inicio del día.
d)
Suponga que la política de la empresa es la de mantener en inventario una
cantidad de producto mínima de 4 toneladas más una cantidad equivalente a
1.25 veces la demanda efectiva del día anterior. La empresa le solicita calcular
el costo de mantenimiento diario del inventario si los costos de alquiler de la
bodega son de $700.000/mes y los de pago de empleados de $500.000/mes.
Adicionalmente se generan unos costos de almacenamiento y mantenimiento de
$100.000 por cada tonelada que amanece en la bodega.
ALGUNAS DISTRIBUCIONES DISCRETAS DE PROBABILIDAD
Ensayo Bernoulli: La variable Aleatoria X define el cumplimiento o no
cumplimiento de una característica en el resultado de un experimento
aleatorio:
X ~ Bernoulli ( p )
1
X =
0
Exito
Fracaso
P ( X = 1) = p
P ( X = 0) = 1 − p = q
Ejemplo de Variables Bernoulli:
1. Lanzamiento de una balón de baloncesto
2. Lanzamiento de una Moneda
3. Aprobación de la Asignatura Estadística
DISTRIBUCIÓN BINOMIAL
Suponga que se repite n veces un ensayo de tipo Bernoulli en donde la
probabilidad de éxito (p) es constante y nos interesa estudiar la variable
aleatoria:
X: # Éxitos obtenidos en las n repeticiones;
X : 0, 1, 2, .…., n
n x
n− x
P ( X = x ) = p ( x ) =   p (1 − p )
 x
E ( X ) = np
Var ( X ) = np (1 − p )
“Numero de éxitos que se esperarían ocurran en los n ensayos
DISTRIBUCIÓN BINOMIAL
Ejemplo: Un experimentado jugador de baloncesto tiene una probabilidad de
acertar en un lanzamiento del 90%. Durante un partido él lanzara 10 veces
al aro, Calcule la probabilidad de que este lanzador obtenga:
a) Que falle en todos sus intentos
b) Exactamente 7 aciertos
c) Un número de aciertos inferior a 2
d) Entre 2 y 4 aciertos
e) No mas de 8 aciertos
f) 2 desaciertos
g) Cual es el número de aciertos que se espera este lanzador obtenga, y
cual su varianza.
DISTRIBUCIÓN BINOMIAL NEGATIVA
Supongamos ahora que nos enfrentamos a repeticiones de ensayos
Bernoulli independientes, (p constante), y que estas repeticiones no se
detendrán hasta que no se completen K éxitos, por tanto nuestra variable
aleatoria seria
X: # ensayos necesarios para obtener K éxitos;
X : k, k+1, + ….
 n − 1 k
n−k
 p (1 − p )
P ( X = n ) = p (n ) = 
 k − 1
k (1 − p )
k
Var ( X ) =
E (X ) =
p2
p
“Numero de ensayos que se esperarían realizar para obtener k exitos”
DISTRIBUCIÓN BINOMIAL NEGATIVA
Ejemplo: En su curso de estadística, su profesor le entrega un conjunto de
ejercicios para que usted los resuelva, de manera que usted solo podrá dejar
de hacer ejercicios hasta tanto no complete un total de 2 ejercicios buenos.
Como usted es un estudiante adelantado, se supone que la probabilidad de
que resuelva un ejercicio es del 75% y que esta no variará de un ejercicio a
otro, calcule la probabilidad de que:
a) Usted necesite un total de 7 ejercicios para terminar la prueba
b) De que usted requiera de una cantidad menor a 3 ejercicios para
culminar
c) Usted requiera menos de 2 ejercicios para culminar
d) La cantidad de ejercicios requeridos para culminar la prueba sea mayor
a4
EJERCICIO
Suponga que usted esta encargado de la recepción de materia prima para cierta
compañía. Para cierto producto especifico, un proveedor ha pactado con la compañía un
porcentaje de unidades defectuosas que no supera el 5%, para la empresa seria
desastroso un lote que con un 8% de unidades defectuosas. La compañía realiza un
pedido semanal de 10.000 unidades y usted está encargado de verificar si el proveedor
efectivamente está cumpliendo con lo pactado. Para ello usted tomará una muestra de
tamaño 50 extraída desde este lote y aceptará el lote solo si observa una cantidad c de
unidades defectuosas. Obviamente la ejecución de esta estrategia presenta dos posibles
errores.
a) Cuales son los errores que pueden generarse
b) Determine el valor de C que garantice un riesgo para el proveedor inferior al 4%.
c) Se supone que el plan debe ser eficiente, de tal manera que permita
rápidamente rechazar un lote con muy malas condiciones. Con el criterio
definido en b cual es la probabilidad de que la inspección requiera de más de 10
unidades inspeccionadas, para un lote que llega con un 10% de unidades
defectuosas.
d) Para la condición evaluada en c, cuantas unidades cree usted que alcanzarían a
inspeccionarse hasta rechazar el lote?
DISTRIBUCIÓN HIPERGEOMETRICA
Suponga que se tiene una población de tamaño N, la cual se divide en dos
subpoblaciones, A de tamaño K y B de tamaño N -K. nuestro interés radica en
tomar una muestra aleatoria de tamaño n de esta población, sin reemplazo, y
contar el número de elementos de la población A presentes en la muestra
X: # elementos de la Población A en la Muestra de tamaño n,
 K  N − K 
 

x  n − x 

P ( X = X ) = p (x ) =
N
 
n
nK
E (X ) =
N
X: 0, 1, 2, 3,…n
N = Tamaño Población
n = Tamaño de la Muestra
K = # elementos de A en la Población
X = # elementos de A en la muestra
Var ( X ) =
nK ( N − K )( N − n )
N 2 ( N − 1)
“Numero de elementos de la población A que se espera tener en la
muestra”
DISTRIBUCIÓN HIPERGEOMETRICA
Ejemplo: una caja contiene 15 bolas, de las cuales 10 son blancas y 5 negras.
Se escoge de manera aleatoria una muestra de 7 bolas. Calcule
a) Probabilidad de obtener exactamente 7 bolas negras.
b) Probabilidad de obtener exactamente 2 bolas negras.
c) Probabilidad de obtener como máximo 3 bolas negras.
d) Probabilidad de obtener entre 3 y 5 bolas negras.
e) El numero esperado de bolas negras que se obtendrían en la muestra
DISTRIBUCIÓN POISSON
Nos interesa modelar el número de eventos ocurridos por unidad
de tiempo, área, volumen.
X: # clientes que ingresan a un almacén en una hora.
Y: # de micro-organismos presentes en un litro de agua.
Z: # de huecos por cuadra en la ciudad de Cali.
e −λ λx
P ( X = X ) = p (x ) =
x!
Estás variables,
generalmente, pueden
modelarse mediante la
distribución poisson
X = {0 ,1, … }
Promedio histórico de eventos por unidad de
tiempo, área o volumen
E (X ) = λ
Var ( X ) = λ
“Número de eventos que se espera ocurran en un intervalo de tiempo, area,
volumen etc.”
DISTRIBUCIÓN POISSON
Ejemplo:
un banco recibe en promedio 6 cheques sin fondo por día, ¿cuáles son las
probabilidades de que reciba,
a) Exactamente cuatro cheques sin fondo en un día dado?
b) Mas de dos cheques sin fondo por día?
c) Exactamente 20 cheques sin fondo en una semana (5 días)?
d) Cual es el número de cheques sin fondos que el banco espera se presenten
diariamente?, cual es su varianza?
DISTRIBUCIONES CONTINUAS
DISTRIBUCIÓN UNIFORME
DISTRIBUCIÓN EXPONENCIAL
DISTRIBUCIÓN NORMAL
DISTRIBUCIÓN GAMMA
DISTRIBUCIÓN BETA
DISTRIBUCIÓN UNIFORME
Definición: Se dice que una variable aleatoria X está distribuida
uniformemente sobre el intervalo [a, b], con a < b, números reales,
si su función de densidad está dada por:
f(x)
“Cualquier valor de X en el rango [a,b] presenta
la misma probabilidad de ocurrencia”
0,2
0,1
x
 1
; si a ≤ x ≤ b

f ( x) =  b - a
 0
; en otro caso
0,0
2
3
a
4
5
6
7
8
9 10 11 12
b
el valor esperado y la varianza vienen dadas por:
a+b
µ = E(X ) =
2
2
(
b
−
a
)
σ 2 = V (X ) =
12
DISTRIBUCIÓN UNIFORME
La función de distribución acumulada F(X)es:
; si x < a
0
x−a

F ( x) = 
; si a ≤ x ≤ b
 b-a
 1 ; si x > b
Ejemplo. Suponga que X se distribuye uniformemente con parámetros a = -3
y b = 2.
a)
b)
c)
d)
¿Cuál es la función de densidad?
¿Cuál es la función de distribución acumulada?
¿Cual es su valor esperado y su varianza?
Calcule
P ( X ≥ 0), P ( − 5 ≤ X ≤ 0.50), P ( X = 0.60)
Distribución triangular
 2( x − a )
 (b − a )( c − a )

 2(c − x )
f ( x) = 
 ( c − b )( c − a )
0,


a≤ x≤b
f(x)
b<x≤c
otro
a
La esperanza es:
a+b+c
E(X ) =
3
b
0,


( x − a) 2

 (b − a )( c − a )
F ( x) = 
2
c
−
x
(
)
1 −
 ( c − b )( c − a )

1
c
x
x≤a
a<x≤b
b<x≤c
x>c
Distribución Exponencial
Generalmente utilizada para modelar tiempos entre eventos
aleatorios (Fiabilidad, Medicina, Logistica).
Su función de densidad de probabilidad está dada por:
λ e − λx
f ( x) = 
 0
x≥0
otro
La fda se define como
0

x
F ( x ) =  λ e − λ t dt = 1 − e − λ x
 ∫0
x<0
x≥0
E(X ) =
V (X ) =
1
λ
1
λ2
Distribución Exponencial
Ejemplo
El tiempo de funcionamiento de cierto componente electrónico es una
variable aleatoria con distribución exponencial, cuya media es de 800 horas.
Suponga que usted ofrece una garantía por un tiempo de servicio equivalente
a 1200 horas.
A) De los próximos 1000 artículos vendidos cuantos presentaran
reclamaciones de garantía?
B) Si el costo de reclamaciones es de 5000 por articulo, cuanto se dinero de
la venta se debe reservar para cubrir las reclamaciones.
C) Suponga que usted solo dispone de 110000. para cubrir garantías, cual
debería ser el tiempo de garantía que debería ofrecer para que el monto de
las reclamaciones no sobrepase este tope.
La Distribución Normal
Sin duda la distribución continua de probabilidad más importante en el campo de la
estadística, por las diversas aplicaciones que se pueden modelar a través de ella.
1
f (x ) =
e
2π σ
 x−µ 
−

 σ 
2
−∞ < x < ∞
Descubierta y publicada por primera vez en 1733 por De Moivre, a la
cual llegaron de manera independiente Gauss(1809) y Laplace (1812)
en relación a la distribución de lo errores en observación astronómica
y física
Que papel juegan el promedio (µ ) y la desviacion (σ) en la
distribución
Ejercicio 1.
Cierto proceso de llenado debe generar botellas de una bebida refrescante con
un contenido nominal de 350 ± 5 cc. Analizando los datos históricos, se ha
encontrado que la distribución de la cantidad llenada en las botellas, cuando el
proceso se encuentra en condiciones habituales de funcionamiento, bien pudiera
seguir una ley normal con promedio de 360cc y varianza de 25 cc.
a) Cual es el porcentaje de botellas con un volumen de llenado no conforme a
las especificaciones?
b) Si un cliente llega a descubrir una botella que contiene un volumen por
debajo de las especificaciones, la empresa estaría obligada a entregar un
bono por valor de $10.000, en promedio cuanto debería reservar la empresa
para asumir los costos de reclamaciones, por cada lote de 10.000 unidades
producidas?
a) Suponga que el proceso ahora se ha descontrolado, llenando a una cantidad
promedio de 350 cc, cual seria el resultado en b?
Corolario:
En consecuencia:
Si
22 − 20
X ~ N (µ = 20; σ = 2 ) ⇒ P ( X < 22) = P( Z <
) = P( Z < 1)
2
1
Valor que se puede obtener desde herramientas computacionales como :
R:
Excel :
pnorm(22,20,2) = pnorm(1,0,1)
DISTR.NORM(22;20;2;1) = DISTR.NORM.ESTAND(1)
O a través del uso de tablas para la distribución normal estándar
DISTRIBUCIÓN NORMAL
0 ≤ Probabilidad ≤ 1
P(Z > a) = 1 − P(Z < a)
P (a < Z < b) = P (Z < a ) − P (Z < b)
P(Z<z) indica acumulación por la
derecha
Continuación…..Para valores positivos
Ejercicio.
a) Supónga que la demanda diaria de agua en la ciudad de cali es una
variable aleatoria con distribución normal con media 50000 litros y varianza de
1600000. ¿Cuanto debe ser la oferta diaria para que la probabilidad de que el
servicio colapse sea menor que 0.03?
DISTRIBUCIÓN NORMAL
(Ejercicio)
Un remache para la industria de la construcción es fabricado para
cumplir con una resistencia al esfuerzo de 2000 psi. Se tiene la
posibilidad de fabricarlos con una de dos maquinas. la primera
produce remaches con una resistencia promedio de 2300 psi y una
desviación de 150 psi. La segunda maquina produce remaches con
resistencia promedio de 2100 psi y desviación de 33.3 psi.
El jefe de producción comenta que no existe espacio suficiente para
mantener las dos maquinas en funcionamiento, por tanto la empresa
debe salir de una de las maquinas. Si lo único en que difieren ambas
maquinas es en la calidad del producto, cual seria su recomendación
para el jefe de producción?
DISTRIBUCIÓN NORMAL
(Ejercicio)
El diámetro interno X de un buje se distribuye normalmente con
media de 20 mm y desviación estándar de 0.4 mm. Los limites de
especificación son 19.2 y 20.9. Si un tubo es no conforme por
debajo, se incurre en un costo interno de rectificación del diámetro
de $ 500. Si el tubo es no conforme por exceso, se envía a
reproceso incurriéndose en una perdida de $1500. Si la utilidad
obtenido por cada tubo conforme que se produce es de $500.
a) ¿Cuál es la utilidad esperada por tubo producido?
b) ¿Cuál es su desviación estándar?
c) ¿Cuánto puede costarle a la empresa la producción de 1000 de
estos tubos?.
Ejercicio.
Un instrumento mecánico producido por cierta empresa, está compuesto por dos
tipos de componentes, dos cojinetes y un eje central, estos componentes son
producidos en 3 maquinarias distintas, obteniéndose una longitud del eje central (X)
que sigue una distribución normal con promedio de 11.2 y desviación estándar de
0.002, mientras que la longitud de los cojinetes sigue una ley normal con promedio
de 0.04 y desviación de 0.001 para Z y 0.003 para Y.
a)
b)
Que porcentaje de los instrumentos tendrían una longitud superior a 12.3?
Cual debería ser el rango de variación tolerable para la longitud del instrumento,
de tal manera que la empresa tenga capacidad de cumplir con un porcentaje
cercano al 95% las unidades producidas?.