Variables Aleatorias y Función de Distribución

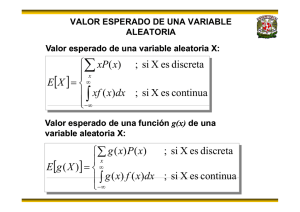
VARIABLES ALEATORIAS Y FUNCIÓN DE
DISTRIBUCIÓN
BIBLIOGRAFIA

Walpole, Ronal E., Myres, Raymond H., Myres,
Sharon L.: Probabilidad y Estadística para
Ingenieros. McGraw Hill-Interamericana.

Canavos G. Probabilidad y Estadística,
Aplicaciones y Métodos. México: Editorial Mc
Graw Hill.
VARIABLES ALEATORIAS
En muchas situaciones, los resultados de un
fenómeno aleatorio son valores no numéricos.
Ejemplo:
Se prueban tres componentes electrónicos, y se
observa si son defectuoso o no.
S  NNN, NND, NDN, DNN, NDD, DND, DDN, DDD
VARIABLES ALEATORIAS
Es conveniente que los resultados de un
experimento
aleatorio
estén
expresados
numéricamente poder responder a preguntas
planteadas con respecto al fenómeno en estudio.
Por lo que se requiere que los resultados de la
observación se registren como valores numéricos,
es decir se asigne un número real a cada uno de los
eventos del espacio muestral.
VARIABLES ALEATORIAS
Ejemplo: Se prueban tres componentes
electrónicos, y se observa si son defectuosos (D)
o no (N).
Se define
defectuosos
X:
Número
de
componentes
VARIABLE ALEATORIA
Definición
Una variable aleatoria es un función que asocia un
número real con cada elemento del espacio
muestral.
X :S 
/ X s   x
Es el conjunto de todos los posibles valores que
puede tomar una variable aleatoria se denomina
Rango de la Variable Aleatoria. Si una variable
aleatoria se denota por X entonces el rango se
denota R X .
RANGO DE UNA VARIABLES ALEATORIAS
X: Número de componentes defectuosos
Eventos de Espacio
Muestral
Valores
de X
NNN
0
X  NNN   0
NND
1
X  NND  X  NDN   X  DNN   1
NDN
1
DNN
1
X  DDN   X  DND   X  NDD  2
DDN
2
DND
2
NDD
2
DDD
3
X  DDD   3
R X  0,1, 2, 3
VARIABLE ALEATORIA
Ejemplos:
 El resultado obtenido al lanzar un dado.
 El número de personas que llegan a un local en
un periodo de tiempo dado.
 El número de piezas defectuosas obtenidas en
una muestra de 200 unidades de un proceso
productivo.
 El tiempo que tardan en ser atendidas las
personas que llegan a un banco.
CLASIFICACIÓN DE VARIABLES ALEATORIAS
Variable Aleatoria Discreta
Si toma sólo un conjunto de valores enteros.
Ejemplos:
 El número de caras en diez lanzamientos de
una moneda
 Número de llamadas telefónicas por hora que
ingresan a un Call Center.
 El número de camiones que llegan por hora al
Puerto del Callao
CLASIFICACIÓN DE VARIABLES ALEATORIAS
Variable Aleatoria Continua
Si toma cualquier valor dentro de un conjunto o
rango de valores.
Ejemplos:
 Peso de recién nacidos
 Tiempo de atención en una agencia bancaria
 Ingreso mensual
VARIABLES ALEATORIAS DISCRETAS
FUNCIÓN DE PROBABILIDAD

La Función de Probabilidad o Función de Densidad
de una variable aleatoria discreta esta dado por:
fX  x   P  X  x 

La función de probabilidad asigna a valor x de la
variable aleatoria X la probabilidad de que X tome
el valor x.

Importante:
fX  x   0

xR X
fX  x   1
FUNCIÓN DE PROBABILIDAD
El conjunto de pares de la forma  x,f X  x   , recibe
el nombre de Distribución de Probabilidad de la
Variable Aleatoria X.
Valores de X
(Rango)
Distribución de Probabilidad de X
Probabilidad de que X tome el valor x
P X  x
0
f X  0   P  X  0  1 8
X
1
fX 1  P  X  1  3 8
fX  x 
2
f X  2   P  X  2  3 8
3
fX  3  P X  3  1 8
Total
 f  x    P X  x   1
R X
X
R X
0
1
2
3
0.125
0.375
0.375
0.125
FUNCIÓN DE PROBABILIDAD
La asignación de probabilidades para la variable
aleatoria están en términos de las probabilidades
de los elementos del espacio muestral S.
FUNCIÓN DE DISTRIBUCIÓN
Si X es una variable aleatoria discreta con
función de probabilidad f X  x , entonces la Función
de Distribución o Función de Distribución
Acumulada esta dado por:
FX  a   P  X  a    P  X  x 
x a
Expresado en términos de la función de
probabilidad FX  a   P  X  a    f X  x 
x a
FUNCIÓN DE DISTRIBUCIÓN
Para variable aleatorias discretas se cumple:
PX  a   PX  a   P X  a 
PX  a   1 PX  a 
PX  a   1 P X  a 
P  a  X  b   FX  b   FX  a 
P  a  X  b   FX  b   FX  a   f X  a 
VALOR ESPERADO Y VARIANZA
Sea X es una variable aleatoria discreta con
función de probabilidad f X  x  entonces:
La media o valor esperado de X es:
E X 

xR X
xf X  x 
La varianza de X es:
V X 
  x  E  X 
xR X
2
fX  x 
VALOR ESPERADO Y VARIANZA
Ejemplo:
X: Número
defectuosos.
X
fX  x 
de
componentes
0
1
2
3
0.125
0.375
0.375
0.125
electrónicos
Distribución de Probabilidad de X
x 3
E  X    xf X  x 
x 0
E  X   0  0.125   1 0.375   2  0.375   3  0.125 
E  X   1.5
VALOR ESPERADO Y VARIANZA
Ejemplo:
X: Número
defectuosos.
X
fX  x 
de
componentes
0
1
2
3
0.125
0.375
0.375
0.125
x 3
electrónicos
Distribución de Probabilidad de X
V  X     x  E  X  fX  x 
2
x 0
V  X    0  1.5   0.125   1  1.5   0.375  
2
2
 2  1.5  0.375   3  1.5   0.125 
2
V  X   0.75
2
VARIABLES ALEATORIAS CONTINUAS
FUNCIÓN DE PROBABILIDAD
La Función de Probabilidad o Función de
Densidad de una variable aleatoria continua es
una función que cumple :
fX  x   0

 f  x  dx  1
X

FUNCIÓN DE DISTRIBUCIÓN
Si X es una variable aleatoria continua con
función de probabilidad f X  x , entonces la Función
de Distribución o Función de Distribución
Acumulada esta dado por:
FX  a   P  X  a  
a
 f  x  dx
X

FUNCIÓN DE DISTRIBUCIÓN
Ejemplo: El contenido de magnesio de una
determinada aleación es una variable aleatoria dada
por la siguiente función de densidad de
probabilidad:
x
0x6

f X  x   18
0 en otro caso
¿Cuál es la probabilidad de que una aleación tenga
un contenido de magnesio entre 2.2 y 4.8?
FUNCIÓN DE DISTRIBUCIÓN
Probabilidad de que una aleación tenga un
contenido de magnesio entre 2.2 y 4.8
P  2.2  X  4.8   FX  4.8   FX  2.2 
4.8
2.2
x
x
P  2.2  X  4.8    dx   dx
18
18


Lo cual es equivalente
P  2.2  X  4.8   0.5055
4.8
x
a: P  2.2  X  4.8    dx
18
2.2
FUNCIÓN DE DISTRIBUCIÓN
Para variable aleatorias continuas se cumple:
PX  a   PX  a 
PX  a   1 PX  a 
P  a  X  b   FX  b   FX  a 
P a  X  b  P a  X  b  P a  X  b
VALOR ESPERADO Y VARIANZA
Sea X es una variable aleatoria continua con
función de probabilidad f X  x  entonces:
La media o valor esperado de X es:
E X 
La varianza de X es:
V X 

 xf  x  dx
X


  x  E  X 

2
fX  x 
FUNCIÓN DE DISTRIBUCIÓN
Ejemplo: El contenido de magnesio de una
determinada aleación es una variable aleatoria dada
por la siguiente función de densidad de
probabilidad:
x
0x6

f X  x   18
0 en otro caso
Calcular, el valor esperado y la varianza
FUNCIÓN DE DISTRIBUCIÓN
Valor esperado del contenido de magnesio

2
x
x
 
E  X    xf X  x  dx   x   dx   dx
18 
18

0 
0
6
6
E X  4
Varianza del contenido de magnesio
V X 

  x  E  X 

V X  2
2
x
f X  x  dx    x  4    dx
 18 
0
6
2
PROPIEDADES DEL VALOR ESPERADO
Sea X y Y dos variables aleatorias y c una
constante real, para toda variable aleatoria se
cumple:
E X  Y  E X  E Y
E c  c
E  cX   cE  X 
E X  c  E X   c
PROPIEDADES DE LA VARIANZA
Sea X y Y dos variables aleatorias y c una
constante real, para toda variable aleatoria se
cumple:
V  X  Y   V  X   V  Y   2Cov  XY 
V c  0
V  cX   c 2 V  X 
V X  c  V X 