3.11 Trasformada de Laplace de una función periódica Definición

3.11 Trasformada de Laplace de una función periódica
246
3.11 Trasformada de Laplace de una función periódica
Definición 3.11.1 Una función f es llamada periódica si y solo si, existe un número no
nulo f tal que siempre y cuando x esté en el dominio de f , también lo esté x + p , y
f ( x + p) = f ( x)
El menor de tales valores positivos de p (si existe) se llama el período de f . Cada una de
las funciones seno, coseno, secante y cosecante tienen periodo 2 L y las otras dos funciones
trigonométricas (tangente y cotangente) tienen período L = π .
Ya que las funciones seno, coseno, secante, cosecante tienen período 2 L , una vez que
conocemos sus valores para 0 < x < 2 L , tenemos todos sus valores; de manera análoga,
puesto que las funciones tangente y cotangente tienen período L , una vez que conocemos
sus valores para 0 < x < L , tenemos todos sus valores.
Las funciones periódicas tienen ciertas propiedades, tales como
sen( x + 2kL) = sen ( x )
cos( x + 2kL) = cos ( x )
sec( x + 2kL) = sec ( x )
csc( x + 2kL) = csc ( x )
tan( x + kL) = tan ( x )
cot( x + kL) = cot ( x )
Donde k es cualquier número entero.
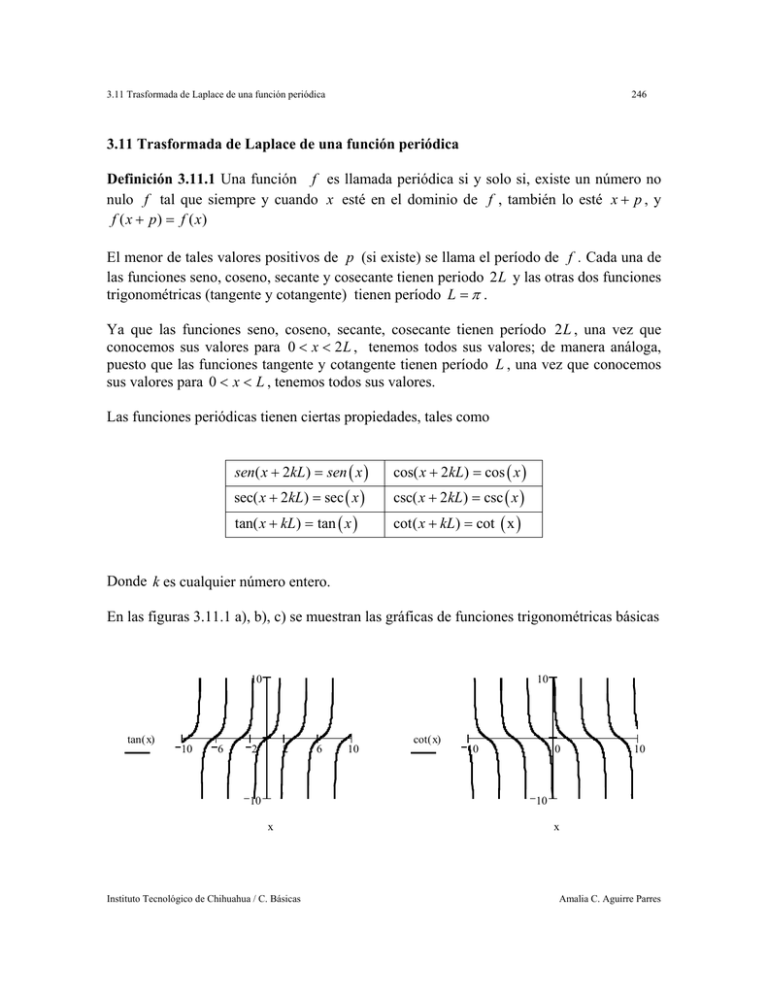
En las figuras 3.11.1 a), b), c) se muestran las gráficas de funciones trigonométricas básicas
10
tan ( x)
10
6
10
2
2
10
6
10
cot ( x)
10
0
10
10
x
Instituto Tecnológico de Chihuahua / C. Básicas
x
Amalia C. Aguirre Parres
3.11 Trasformada de Laplace de una función periódica
247
Figura 3.11.1 a) tan( x), cot( x)
2
sin( x)
10
5
2
0
5
10
cos( x)
10
5
0
2
5
10
2
x
x
Figura 3.11.1 b) sen( x), cos( x)
10
sec( x)
10
5
10
0
5
10
csc( x)
10
10
6
2
2
6
10
10
x
x
Figura 3.11.1 c) sec( x), csc( x)
Figura 3.11.1 Funciones trigonométricas básicas
En la gráficas de las figuras 3.11.1 se puede apreciar la periodicidad de las funciones, con
período 2 L , así el que las funciones sean pares o impares, por su simetría con el eje y , o
con el origen.
Instituto Tecnológico de Chihuahua / C. Básicas
Amalia C. Aguirre Parres
3.11 Trasformada de Laplace de una función periódica
248
Extender periódicamente una función es tomar el segmento de la gráfica que se quiere
extender e ir repitiéndolo de acuerdo al período de dicho segmento de la gráfica.
Transformada de Laplace de una función periódica
Si el período de una función periódica es T , entonces f (t + T ) = f (t ) . Se puede
determinar la transformada de Laplace de una función periódica mediante la integración de
un período.
Teorema 3.11.1 Si f (t ) es continua por tramos en (0, ∞) , de orden exponencial y
periódica con periodo T ,
L { f (t )} =
1
(1 − e
− sT
)∫
T
o
e − st f (t )dt
(1)
f(t)
t 0 ≤ t < 1
Ejemplos 3.11.1 Determine la transformada de Laplace de la función f (t ) = 
0 1 ≤ t < 2
de período T = 2 , cuya gráfica es
5
4
3
2
1
0 1
2
3
4
5
t
Figura 3.11.2 Diente de Sierra
Utilizando (1) del teorema 3.11.1 Por propiedades de integral tenemos que
Instituto Tecnológico de Chihuahua / C. Básicas
Amalia C. Aguirre Parres
3.11 Trasformada de Laplace de una función periódica
L { f (t )} =
1
1 − e −2 s
O bien L { f (t )} =
(∫ e
1
− st
0
2
249
(t )dt + ∫ e− st (0)dt
1
1 − e −2 s
Haciendo u = t y dv = −
1
1
∫ te
− st
0
)
(2)
dt
1 − st
1
e (− s )dt , entonces du = dt y v = − e − st
∫
s
s
Por lo que su integral sería
1
  1 − st   1  − st 
L { f (t )} =
t − e
e dt 
− −
−2 s  

(1 − e )   s   s  ∫
Después de integrar (3), tenemos L { f (t )} =
(3)
 t − st 1 − st 
− e − 2e 
−2 s 
s

(1 − e )  s
1
1
0
Sustituyendo los límites
L { f (t )} =
1
(1 − e
−2 s
 1 − s (1) 1 − s(1)   0 − s ( 0) 1 − s( 0)  
− e
− 2e
− 2e
 −− e

s
s
  s

)  s
Simplificando L { f (t )} =
L { f (t )} =
L { f (t )} =
1
(1 − e
−2 s
 1 − s 1 − s   1
− e − 2 e  −− 2
s
  s
(1 − e−2 s )  s
1
 1 −s 1 −s 1
− e − 2e + 2
s
s
)  s
 e− s 1 − e− s 
−
+
(1 − e−2 s )  s s 2 
1




 , finalmente

(4)
Ejemplo 3.11.2 Encontrar la transformada de Laplace de la función diente de sierra que se
muestra en la figura.3.11.3
Instituto Tecnológico de Chihuahua / C. Básicas
Amalia C. Aguirre Parres
f(t)
3.11 Trasformada de Laplace de una función periódica
250
a
b
2b
t
Figura 3.11.3 Diente de sierra con periodo T = b
En la gráfica de la figura 3.11.3 podemos observar que f (t ) =
periodo T = b , por lo tanto aplicando la fórmula (1)
L { f (t )} =
 b − st  a  
e
t dt
(1 − e−bs )  ∫0  b  
1
Integrando L { f (t )} =
L { f (t )} =
a
a−0
t , dado que m =
, el
b
b−0
1
(1 − e
− bs
(5)
b
 a   t − st 1 − st 
− e − 2 e  , sustituyendo límites
− bs 
s
0
(1 − e )  b   s
1
 a   b − bs 1 −bs   0 − s( 0) 1 − s( 0)  
− e − 2 e  −− e
− 2e

s
s
  s

)  b   s
Simplificando L { f (t )} =
Factorizando L { f (t )} =
1
(1 − e
1
(1 − e
Reacomodando L { f (t )} =
− bs
− bs
(6)
 a   b − bs 1 − bs 1 
− e − 2e + 2
s
s 
)  b   s
 a   b − sb 1
− sb 
   − e + 2 (1 − e ) 
s

) b  s
− ae − sb
a 1
+
  2 , finalmente
s (1 − e −bs )  b  s
Instituto Tecnológico de Chihuahua / C. Básicas
Amalia C. Aguirre Parres
3.11 Trasformada de Laplace de una función periódica
L { f (t )} =
251
−a
a 1
+  2
s ( e − 1)  b  s
(7)
sb
Ejemplo 3.11.3 Encontrar la transformada de Laplace de la función onda cuadrada
1 0 < t < a
f (t ) = 
con periodo T = 2a
0 a < t < 2a
f(t)
2
1
a
2a
3a
t
Figura 3.11.4 Onda Cuadrada con periodo a
De tal manera que la transformada de Laplace sería
L { f (t )} =
1
(1 − e
− s( 2 a )
e
) (∫
Por lo que L { f (t )} =
a
− st
0
2a
(1)dt + ∫ e − st (0)dt
a
)
(8)
 1 a − st

− ∫ e (− s )dt  , integrando
−2 as 
0

(1 − e )  s
1
a
 1 − st 
, sustituyendo límites
L { f (t )} =
− e
−2 as 
(1 − e )  s  0
1
Instituto Tecnológico de Chihuahua / C. Básicas
Amalia C. Aguirre Parres
3.11 Trasformada de Laplace de una función periódica
L { f (t )} =
L { f (t )} =
1
(1 − e
−2 as
1
(1 − e
−2 as
252
 1 − s ( a )    1 − s ( 0 ) 
− e
− − e
)  s   s 
1
 1 − as 1 
1
1 − e − as )
(
 − e +  , simplificando L { f (t )} =  
−2 as
s
s
s

  (1 − e )
)
Descomponiendo el denominador (1 − e −2 as ) en binomios conjugados (1 − e − as )(1 + e − as )
1
1
Resulta L { f (t )} =  
 s  (1 + e − as )
Ejemplo 3.11.4 Encontrar la transformada de Laplace de la función meandro que se
muestra en la figura 3.11.5
1 0<t<a
f (t ) = 
con periodo T = 2a
 −1 a < t < 2a
2
f(t)
1
a
2a
3a
4a
1
2
t
Figura 3.11.5 Función meandro
De tal manera que la transformada de Laplace sería
Instituto Tecnológico de Chihuahua / C. Básicas
Amalia C. Aguirre Parres
3.11 Trasformada de Laplace de una función periódica
L { f (t )} =
1
(1 − e
() ∫ e
a
− s( 2 a )
− st
253
2a
(1)dt + ∫ e− st (−1)dt
a
0
1
 1 a − st

 1  2 a − st
 − s ∫0 e (− s )dt −  − s  ∫a e (− s )dt 
 


Por lo que
L { f (t )} =
Resultando
 1 − st
L { f (t )} =
− e
(1 − e−2as )  s
(1 − e
− s( 2 a )
)
1
Sustituyendo límites L { f (t )} =
Factorizando
)
1
(1 − e
−2 as
a
0
1
+ e− st
s
2a
a



 1 − as 1   1 −2 as 1 − as  
− e + + e
− e 
s s
s

)  s
1
1
y simplificando L { f (t )} =
−2e − as + 1 + e −2 as )
(
−2 as
s
s (1 − e )
El segundo factor corresponde a un binomio al cuadrado por lo que
L { f (t )} =
1
s (1 − e
−2 as
)
(1 − e )
− as 2
Descomponemos en binomios conjugados el denominador
L { f (t )} =
s (1 − e
1
− as
)(1 + e )
− as
(1 − e )
− as 2
(1 − e )
Simplificando L { f (t )} =
s (1 + e )
− as
− as
Ejemplo 3.11.5 Encontrar la transformada de Laplace de la función
f (t ) = sen ( t ) para 0 < t < π , con periodo T = π , que se muestra en la figura 3.11.5
Instituto Tecnológico de Chihuahua / C. Básicas
Amalia C. Aguirre Parres
3.11 Trasformada de Laplace de una función periódica
254
f(t)
2
1
t
π
2π
3π
Figura 3.11.5 f (t ) = sen ( t ) para 0 < t < π , con periodo T = π
De tal manera que la transformada de Laplace sería aplicando (1)
L { f (t )} =
(
1
1− e
{) ∫ e
π
− s (π )
0
− st
 sen ( t )  dt
}
(9)
Aplicando la fórmula de la integral
∫
e au sen ( bu ) du =
e au
 asen ( bu ) − b cos ( bu ) 
a 2 + b2 
(10)
Por lo que
L { f (t )} =
 e − st

 − s sen ( t ) − cos ( t )  
−π s  2
(1 − e )  s + 1

1
π
(11)
0
Sustituyendo límites de la integral en (11)

   e −π s
 
  e − s( 0)
1

s
sen
cos
s
sen
0
cos
0
π
π

−
−

−

−
−

L { f (t )} = 
(
)
(
)
(
)
(
)








 
2
2
 (1 − e −π s )    s + 1
  s + 1

Instituto Tecnológico de Chihuahua / C. Básicas
Amalia C. Aguirre Parres
3.11 Trasformada de Laplace de una función periódica
255
Simplificando

   e −π s
  1
1


1
1
+
−
−
L { f (t )} = 
[
]
[
]






2
2

 (1 − e −π s )    s + 1
 s +1
(12)
En MathCad la evaluación de la integral (9)
1
1
e
π .s
.
π
e
0
s t.
1
sin ( t ) d t
s
2
exp( π . s )
1 .( 1
exp( π . s ) )

  e −π s
1
1 

 2
+ 2
Reacomodando L { f (t )} =
,
−π s
 (1 − e )   s + 1 s + 1 
Simplificando
−π s
1  (1 + e ) 


L { f (t )} = 2
s + 1  (1 − e −π s ) 


Instituto Tecnológico de Chihuahua / C. Básicas
(13)
Amalia C. Aguirre Parres