Ejercicio 1

Introducción a la Economía I – Cátedra a Distancia
Unidad 9
Ejercicio 1
Sabemos que en un modelo de economía cerrada y sin gobierno, el ingreso de las
familias se aplica en el consumo de bienes o se ahorra:
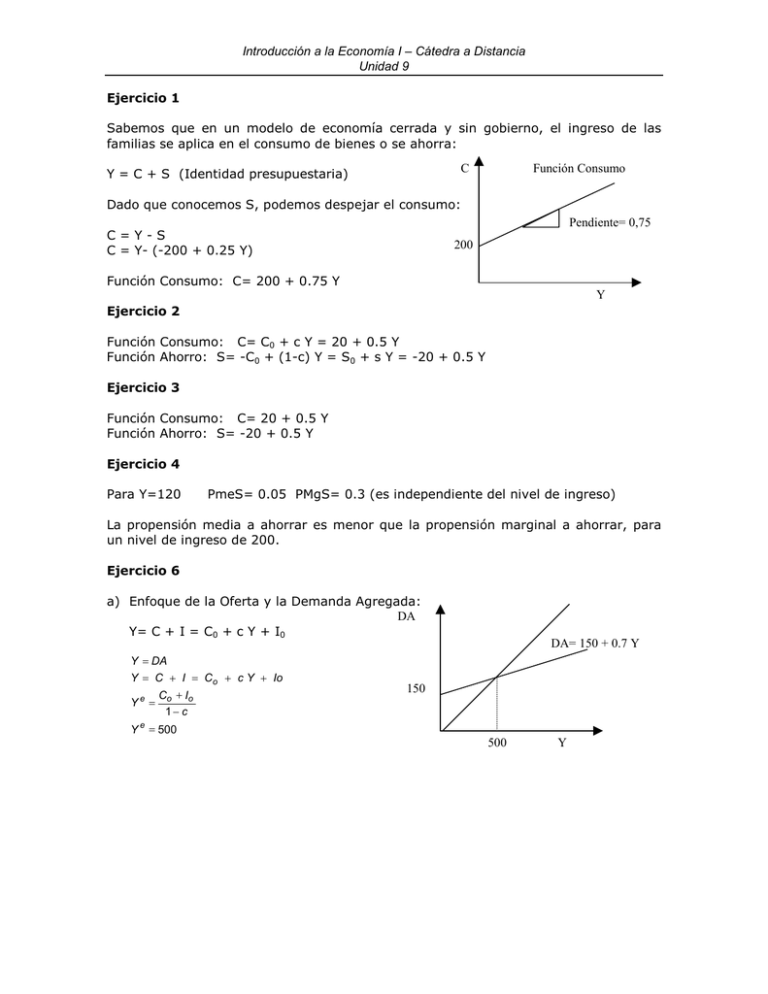
Función Consumo
C
Y = C + S (Identidad presupuestaria)
Dado que conocemos S, podemos despejar el consumo:
Pendiente= 0,75
C=Y-S
C = Y- (-200 + 0.25 Y)
200
Función Consumo: C= 200 + 0.75 Y
Y
Ejercicio 2
Función Consumo: C= C0 + c Y = 20 + 0.5 Y
Función Ahorro: S= -C0 + (1-c) Y = S0 + s Y = -20 + 0.5 Y
Ejercicio 3
Función Consumo: C= 20 + 0.5 Y
Función Ahorro: S= -20 + 0.5 Y
Ejercicio 4
Para Y=120
PmeS= 0.05 PMgS= 0.3 (es independiente del nivel de ingreso)
La propensión media a ahorrar es menor que la propensión marginal a ahorrar, para
un nivel de ingreso de 200.
Ejercicio 6
a) Enfoque de la Oferta y la Demanda Agregada:
DA
Y= C + I = C0 + c Y + I0
DA= 150 + 0.7 Y
Y = DA
Y = C + I = Co + c Y + Io
Ye =
Co + I o
1− c
150
Y e = 500
500
Y
Introducción a la Economía I – Cátedra a Distancia
Unidad 9
Enfoque de filtraciones y gastos compensatorios
S, I
S =I
S0 + s Y = I0
S= -100 + 0,3 Y
Y = 500
e
Io= 50
c) S= 20
500
Y
-100
Ejercicio 7
DA= OA
DA
a) Ye= 17.000
Exceso de Oferta = VE (+)
c) OA-DA = VE
20.000 – [3400 + 0.8 (20.000)]= VE
600 = VE
19.400
DA
3400
DA= 3400 + 0.8 Y
17.000
20.000
Y
S = Io + VE
-3000 + 0.2 (20.000) – 400 = VE
600= VE
Filtraciones = Gastos Compensatorios
S= -3000+ 0,2 Y
S, I
Ahorro planeado – Inversión planeada = VE
Io= 400
17.000 20.000
Y
Ejercicio 8
De acuerdo al enunciado, los datos disponibles son los siguientes: Se trata de una economía
cerrada, sin sector público en la que
Co = 180; Io = 200; si Y = 600 el S = 0 (C = Y).
Introducción a la Economía I – Cátedra a Distancia
Unidad 9
Se nos pide:
Determinar la función consumo correspondiente a dicha economía.
Trabajamos con una función consumo lineal, que puede representarse a través de una ecuación
del tipo:
C = Co + c Y
El consumo autónomo (Co) es un dato, pero no conocemos el valor de la propensión marginal a
consumir (PMgC) representada por “c”. Sabemos que la PMgC es el cambio en el consumo por
cada unidad monetaria que varíe el ingreso:
c = ∆C / ∆ Y, para calcularla podemos expresar la función consumo a través de
una tabla, según los datos conocidos:
Y
0
600
C
180
600
El consumo autónomo es el consumo para un nivel de ingreso nulo que, en este caso es igual a
180. Sabemos que cuando el ingreso es de 600, el ahorro es igual a cero, y dado que el ingreso
es igual al consumo más el ahorro, entonces si el ahorro es cero el consumo es igual al ingreso.
Dados dos niveles de ingreso y sus correspondientes consumos (variables medidas en unidades
monetarias), podemos calcular la PMgC (que es constante para el caso de funciones de consumo
lineales, debido a que es la pendiente de la función).
PMgC = ∆C / ∆ Y
c = 420 / 600
c = 0,70
Esto significa que el consumo varía en $ 0,70 por cada unidad monetaria en que varía el ingreso.
Los $0,30 restantes se destinan a ahorro (la propensión marginal a ahorrar –PMgS-, en este
caso es igual a 0,30).
Entonces,
C = 180 + 0,70 Y
Calcular el ingreso de equilibrio.
Si aplicamos la fórmula de cálculo (derivada de cualquiera de las condiciones que debe cumplir
el ingreso para ser de equilibrio),
Ye = Co + Io
1–c
a la suma de los componentes autónomos de la demanda agregada, se los puede sumar ya que
están expresados en unidades monetarias, obteniendo el gasto agregado autónomo (o demanda
agregada autónoma).
Ye
=
GAo / (1 – c)
Ye = 380 / 0,30
Ye = $1.266,67
Calcular la PMeS (propensión media a ahorrar), para el ingreso de equilibrio.
Definimos la PMeS como la relación entre el ahorro de las familias con respecto al nivel de
ingreso de la economía y mide la proporción del ingreso que se destina a ahorro.
PMeS = S / Y,
Al ahorro correspondiente al ingreso de equilibrio lo podemos calcular como:
S=Y–C
Introducción a la Economía I – Cátedra a Distancia
Unidad 9
S = 1.266,67 – (180 + 0,70 . 1.266,67)
S = 1.266.67 - 1.066,67
S = $200;
idéntico resultado se obtiene aplicando la ecuación correspondiente a la función ahorro:
S = - Co + (1 – c) Y;
S = - 180 + 0,30 . 1.266,67
S = - 180 + 380
S = $200
Calcular la variación de existencias para un ingreso de 1.400 (por los dos métodos conocidos).
Ya hemos calculado el ingreso de equilibrio por lo tanto sabemos que si Y = 1.400 > 1.266,67 y
existirá una acumulación de stocks no deseada (variación de existencias no planeadas positiva,
VE>0). El monto al que asciende la variación de existencias puede obtenerse por dos métodos:
a) VE = OA – DAp
b) VE = Filtraciones – Gastos Compensatorios
VE =
S
-
Io
Aplicando el método a), debemos obtener la demanda agregada planeada para Y = 1.400.
DAp = C + Io, reemplazando al C por su ecuación:
DAp = Co + cY + Io
DAp = Co + Io + cY
DAp = GAo + cY; siendo ésta la función DAp. En este caso se trata de una
función lineal, con pendiente positiva e igual a la PMgC (c), y cuya ordenada al origen (la DAp
para un Y = 0) igual a la sumatoria de los componentes autónomos de la demanda agregada
planeada. Reemplazando en la función por los datos del ejercicio:
caso en que
Y = 1.400;
DAp = 380 + 0,70 Y (función DAp para cualquier nivel de ingreso) y para el
DAp = 380 + 0,70 . 1400
producto;
DAp = 1.360
VE = OA – DAp, siendo la oferta agregada igual al nivel de ingreso o
VE = 1.400 – 1.360
VE = $40.
Aplicando el método b), debemos calcular el ahorro de las familias correspondiente a Y = 1.400,
para lo cual podemos aplicar la ecuación correspondiente:
S = - 180 + 0,30 . 1400
S = 240
VE = S – Io
Introducción a la Economía I – Cátedra a Distancia
Unidad 9
VE = 240 – 40
VE = 40
Observamos que el valor obtenido es el mismo cualquiera sea el método adoptado.
Si bien no es una consigna de este ejercicio, vamos a aprovechar lo hecho hasta ahora para
calcular la inversión y la demanda agregada realizadas.
La inversión realizada es igual a la inversión planeada más la inversión no planeada (variación
de existencias), entonces:
Irealizada = Io + VE
Irealizada = 200 + 40
Irealizada = 240
Comparando el valor de la inversión realizada y el ahorro, observamos que son iguales. La
igualdad entre ahorro e inversión realizada se da para todo nivel de ingreso; mientras que la
igualdad entre ahorro e inversión planeada se da sólo para el ingreso de equilibrio.
S = Irealizada para todo Y
S = Io sólo para Y = Ye
Una vez conocida la inversión realizada podemos obtener la demanda agregada realizada ya que
ésta es igual al consumo más la inversión realizada
DA realizada = C + Io + VE
DA realizada = C + Irealizada, o también
DA realizada = DAp + VE
DA realizada = 1.360 + 40
DA realizada = 1.400
Comparando la demanda agregada realizada con la oferta agregada o ingreso, observamos que
ambas son iguales.
La igualdad entre demanda agregada realizada y oferta agregada se da para todo nivel
de ingreso; mientras que la igualdad entre oferta agregada y demanda agregada
planeada se da sólo para el ingreso de equilibrio.
OA = DA realizada; para todo Y
DA
OA = DAp; sólo para Y = Ye
Exceso de Oferta = VE (+)
DA
380
DA = 380 + 0.7 Y
1266,7
1400
Y
Introducción a la Economía I – Cátedra a Distancia
Unidad 9
Ejercicio 9
a) S + T = I + G
S0 + s Y + T0 = I0 + G0
Ye= 780
b) Se debe verificar la identidad OA= DA
Y = 150 + 0.7 ( Y – 80) + 60 + 80
Reemplazando a Y por su valor obtenido en a) llegamos a la identidad
780 = 780
c) VE= -84 (Exceso de demanda)
d) T’= G’= 100 ; Ye= 800; El ingreso ha variado en la misma magnitud en que varió
el gasto (= variación en impuestos= 20).
Ejercicio 10
Suponga una economía con la siguiente información:
C = 100 + 0,80 Yd
Yd = Y – To
To = 200 ; Io = 200; Go = 200
De acuerdo con los datos del enunciado, se supone una economía cerrada con sector público. La
intervención del sector público se manifiesta a través del cobro de impuestos (T) y la realización
del gasto (Go). Ambos factores (impuestos y gastos) afectan la demanda agregada de la
economía. En el caso del gasto del gobierno, resulta obvio que es un componente del gasto
agregado de la economía. En el caso de los impuestos, éstos afectan la demanda agregada a
través del consumo de las familias. Como sabemos, la parte del ingreso que las familias pueden
destinar a consumo o a ahorro, es el ingreso disponible. Dados los supuestos de este modelo,
enunciados más arriba, la diferencia entre ingreso nacional y disponible son los impuestos.
Es decir que una parte del ingreso que las familias hubieran destinado a consumo o a ahorro,
deberán destinarla a pagar impuestos. Con respecto a la situación “sin impuestos”, es decir
cuando tanto el consumo como el ahorro eran función del ingreso nacional, ambos se verán
reducidos. La reducción en el consumo dependerá del monto del impuesto y de la propensión
marginal a consumir. Sólo la proporción que representa la PMgC, hubiera sido la parte del
impuesto que se hubiera destinado a consumo. Del mismo modo, la reducción en el ahorro será
igual a la parte del tributo que se hubiera ahorrado, es decir que depende no sólo del monto del
impuesto sino también de la propensión marginal a ahorrar.
Así si To = 200, PMgC (c) = 0,80; de los $200 que se destinan a pagar impuestos $160 se
hubieran gastado en bienes de consumo; el resto, $40, no se hubieran consumido sino que se
hubieran ahorrado (PmgS. To = 0,20 . 200 =$40).
Resolveremos los items de este ejercicio algebraicamente, donde se nos pide encontrar:
a) La función ahorro.
b)
A partir de la función consumo dada deducimos la correspondiente función ahorro:
Introducción a la Economía I – Cátedra a Distancia
Unidad 9
S
S
S
S
S
=
=
=
=
=
-
Co
100
100
100
140
+PmgS Yd
+ 0,2 (Y – T)
+ 0,2 (Y – 200)
+ 0,2 Y – 40
+ 0,2 Y;
S (Y)
S
S(Yd)
500
700
Y
-100
- 140
La función ahorro queda expresada en función del ingreso nacional y no del ingreso disponible.
El impuesto, afecta la ordenada al origen de la función, que es menor que en la situación sin
impuestos, en cuyo caso el ahorro correspondiente a un ingreso igual a cero ( que, por ser
negativo, implica un desharro) hubiera sido igual a – 100.
En el gráfico hemos representado las funciones de ahorro correspondientes a la situación “antes”
y “después” del impuesto. La segunda se ha desplazado en $40 con respecto a la primera,
siendo ese monto la magnitud en que disminuyó el ahorro como consecuencia del impuesto.
c)
El ingreso de equilibrio.
Aplicando la fórmula correspondiente al ingreso de equilibrio, cuya deducción puede ser leída en
la bibliografía básica, obtenemos el mismo, de la siguiente manera:
Ye
GAo
= -----------------1–c
Co + Io + Go – cTo
Ye = ______________________ =
1–c
Ye =
Ye =
Ye =
100 + 200 + 200 – 0,8 . 200
____________________________=
0,20
340 / 0,20
$1.700
c) El valor del multiplicador.
El multiplicador del gasto público autónomo o el de la inversión autónoma es igual a:
k Go ó Io = 1 / 1 – c
k Go ó Io = 1 / 0,2
k Go ó Io = 5
Esto significa que por cada unidad monetaria que aumente Io o Go, el ingreso de equilibrio
aumentará 5 unidades monetarias. De las 5 unidades monetarias en que aumenta el ingreso de
equilibrio, 1 unidad se explica por el aumento en el componente autónomo de la demanda
agregada (Io ó Go); las 4 unidades restantes representan los efectos sucesivos de los aumentos
en el Ye sobre el consumo de las familias.
El multiplicador del impuesto autónomo es igual a:
k To = - c / 1 – c
k To = - 0,8 / 0,2
k To = - 4;
Introducción a la Economía I – Cátedra a Distancia
Unidad 9
En este caso el valor del multiplicador indica en cuántas unidades monetarias disminuye
(aumenta) el ingreso de equilibrio por cada unidad monetaria en que aumenta (disminuye) los
impuestos autónomos. Por cada $1 en que aumenta To, el ingreso disponible disminuye en $1 y
el consumo en $0,80; pero al disminuir el consumo disminuye el ingreso disponible lo que
ocasiona una nueva caída en el ingreso y así sucesivamente hasta llegar a $5 el efecto total
sobre el ingreso de equilibrio.
Vemos que la relación entre cambios en los impuestos autónomos y variación en el ingreso de
equilibrio es inversa. Esto es por los efectos que los impuestos tienen sobre la demanda
agregada a través del consumo.
d) ¿Qué sucedería si el valor del producto fuese de 2000?
e)
Este valor es mayor que el ingreso de equilibrio calculado en el punto b, (Ye= 1.700), por lo
tanto un Y=2.000 no corresponde a una situación de equilibrio, existiendo variación de
existencias no planeada positiva.
Como en el ejercicio 8, la variación de existencias no planeadas (o no deseadas) pueden
calcularse a través de los dos métodos planteados.
1.
V.E = OA – DAp
La oferta agregada es siempre igual al ingreso. Debemos calcular la Dap para Y= 2.000. Para
ello partimos de la ecuación correspondiente
DAp = Gao + c Y
DAp = 340 + 0,80 . 2.000
DAp = 1.940
VE
= 2.000 – 1940
VE
= 60
OA = Y
Dap
VE
OA
E
1700
340
0
1700
2000
Y
Gráficamente, la diferencia entre la recta de 45° (línea de puntos) y la curva de demanda
agregada, representa la variación de existencias, en este caso positiva e igual a 60 unidades
monetarias.
2. El ingreso de equilibrio cumple con la igualdad entre filtraciones y gastos compensatorios; si
la oferta agregada de la economía es mayor o menor que la demanda agregada planeada, el
ingreso no es de equilibrio y la igualdad mencionada no se cumple. En ese caso la diferencia
Introducción a la Economía I – Cátedra a Distancia
Unidad 9
entre filtraciones y gastos compensatorios es igual a la variación de existencias. En el
modelo de economía cerrada, con sector público, el ahorro de las familias y los impuestos
constituyen las filtraciones mientras que la inversión y el gasto público son los gastos
compensatorios.
Filtraciones = Gastos Compensatorios
Sf + T
=
Io + Go;
Haciendo un pasaje de términos y dado que la diferencia entre ingresos del gobierno (T) y sus
gastos (Go), constituyen el ahorro del sector, podemos expresar la igualdad anterior tal como
sigue:
Sf + (T – Go) =
SG
=
Sf +
Io
Io
Cuando el ingreso no es de equilibrio, esta igualdad no se verifica y la diferencia entre ambos
miembros constituye la variación de existencias.
En el caso planteado en el ejercicio, para un ingreso de 2.000,
Sf = - 140 + 0,2 . 2.000
Sf = 260; luego
260 + 200 > 200 + 200
260 + (200 – 200) – 200 = VE
60 = VE
Una vez calculada la variación de existencias para un Y = 2.000, podemos calcular la inversión y
la demanda agregada realizadas para dicho ingreso:
I realizada = Io + VE
I realizada = 200 + 60
I realizada = 260 = (SF + SG) = (ahorro de la economía)
DA realizada = C + Io + VE + Go; siendo Io + VE = Irealizada
Da realizada = DAp + VE
DA realizada = 1940 + 60
DA realizada = 2.000 = OA
f)
¿Qué podría hacer el gobierno para llevar el ingreso (de equilibrio) a 2.500?
En este caso, el gobierno debería aplicar una política fiscal expansiva, con el objetivo de
aumentar el nivel de actividad (producto) y consecuentemente de empleo en la economía. Para
ello el gobierno podrá:
Aumentar el gasto público autónomo (∆ Go),
•
•
Disminuir los impuestos autónomos (∇ To),
•
Aumentar el gasto público autónomo y los impuestos autónomos en un mismo monto
(∆Go = ∆ To), manteniendo el presupuesto equilibrado.
Partiendo de la situación de equilibrio, es decir de un Ye = 1.700; se pretende incrementarlo en
800.
Introducción a la Economía I – Cátedra a Distancia
Unidad 9
Un aumento en Go, provocará un aumento en igual magnitud en la demanda agregada planeada
de la economía y tendrá un efecto multiplicador sobre el consumo. No será necesario un
aumento del Go en 800, sino en menor magnitud. Dado que
∆Go ⇒ ∆Ye = kG ∆Go;
Reemplazando a ∆Ye y kG por los valores conocidos;
800 = 5∆Go ; despejando,
800/5 = 160
Este resultado significa que, un aumento de 160 unidades monetarias en el gasto público
permitirá lograr un aumento de 800 u.m. en el ingreso de equilibrio, correspondiendo 640 u.m a
los aumentos sucesivos sobre el nivel de consumo, debido al efecto multiplicador.
Si se opta por reducir impuestos autónomos, se logrará un aumento del ingreso de equilibrio
porque el ingreso disponible de las familias se verá incrementado en el mismo monto en que se
reduzcan los impuestos, aumentará el consumo y el ingreso, provocando también un efecto
multiplicador sobre el gasto de la economía.
∆Ye = kT ∆To;
800 = (-4) ∆To
800/(-4)= -200
Ello implica que, una reducción en los impuestos autónomos de 200 unidades monetarias
provocará, en primera instancia, un aumento en el consumo de las familias en 160 u.m; y
aumentos sucesivos sobre este mismo componente de la demanda agregada, hasta un monto
total a 800 u.m.
Finalmente el gobierno, puede desear no incurrir o no aumentar el déficit de su presupuesto
(T- G), financiando un aumento en el gasto público con un incremento de igual monto en los
impuestos, en este caso, y como demostramos más arriba, operaría el multiplicador del
presupuesto equilibrado, que asume un valor igual a uno, en el modelo con el que estamos
trabajando. Si el multiplicador conjunto (del aumento en Go y en To) es la unidad, entonces
para aumentar el ingreso de equilibrio en 800 u.m se deberá aumentar el gasto público y los
impuestos autónomos en 800 unidades monetarias.
∆Go = ∆To = ∆Ye;
800 = 800 = 800
Podemos corroborar este resultado, sumando los efectos que ambas medidas tienen sobre el Ye.
∆Go⇒ ∆ Ye = 5 . 800
∆Go⇒ ∆ Ye = 4.000 u.m
∆To⇒ ∇ Ye = -4. 8.000
∆To⇒ ∇ Ye = - 3.200; sumando ambos efectos:
∆ Ye = 4.000 – 3.200
∆ Ye = 800
f) ¿Cuál sería el ingreso de equilibrio si T = 200 + 0,1 Y?
La ecuación planteada para los impuestos supone la existencia de impuestos autónomos (To) por
un valor fijo de 200 unidades monetarias y un impuesto proporcional sobre el nivel de ingreso
(tY), siendo la alícuota impositiva (t) del 10% del ingreso.
Introducción a la Economía I – Cátedra a Distancia
Unidad 9
En este caso el ingreso disponible de las familias es igual a:
YD = Y – T
y el consumo:
YD = Y – (To + t Y)
C = f (YD )
C = Co + c {Y - (To + t Y)}
Operando algebraicamente, se llega a una expresión para la función consumo tal como:
C = Co – cTo + c (1 – t) Y; siendo (Co – cTo) la ordenada al
origen y c (1 –t) la pendiente de la función.
Podremos obtener la función ahorro correspondiente, a partir de la diferencia entre ingreso
disponible y consumo. Es decir que en este caso las familias destinan su ingreso a impuestos,
ahorro y consumo. La expresión correspondiente a la función ahorro, es la siguiente:
S = f (YD )
S=Y–T–C
S = YD - C
S = - Co – (1 – c) To + (1 – c) (1 – t) Y
Siendo {- Co – (1 – c) To}, la ordenada al origen y (1 – c) (1 – t) la pendiente de la función
ahorro.
Se puede deducir la fórmula para el nivel de ingreso que cumple las dos condiciones de
equilibrio,
Ye = GAo / 1 – c (1 – t)
Ye = GAo / 1 – c + c t;
Reemplazando por los datos del ejercicio:
Ye = 340 / 1 – 0,80 + 0,80 . 0,10
Ye = 340 / 0,28
Ye = 1.214,28 u.m
El valor del ingreso de equilibrio obtenido es menor que el calculado en a); esto se debe a la
incorporación del impuesto proporcional que al disminuir el ingreso disponible provoca una
reducción en el consumo de las familias y por lo tanto en el producto de la economía.
La verificación de que el valor obtenido es de equilibrio, consiste en comprobar que se cumplan
ambas condiciones;
O.A = D.Ap y
S + T = Io + Go, ó (SF + S G = Io)
D.Ap = C (YD ) + Io + Go
D.Ap = GAo + c (1 – t) Y
D.Ap = 340 + 0,72 Y
D.Ap = 340 + 0,72 . 1.214,28
Introducción a la Economía I – Cátedra a Distancia
Unidad 9
D.Ap = 340 + 874,28
D.Ap = 1.214,28;
El valor obtenido para D.Ap es igual al valor del Ye, con lo cual se verifica una de las condiciones
de equilibrio.
Comprobemos ahora la segunda condición:
S + T = Io + Go, ó (SF + S G = Io):
SF = - 100 + 0,20 (1.214,28 – 200 - 0,10 . 1.214,28)
SF = - 100 + 0,20 . 892,86
SF = 78,58
SF + T = Io
78,58 + 321,42 = 400;
Esta condición también puede expresarse a través de la igualdad entre ahorro de la economía e
inversión planeada:
78,58 + 121,42 = 200
200 = 200;
Quedando verificadas ambas condiciones de equilibrio.
g) ¿Cuál sería el ingreso de equilibrio si X = 300 y M = 0,10 Y?
En este apartado suponemos una economía abierta. Se incorpora un nuevo componente de la
demanda agregada autónoma al incluir a la demanda externa de bienes producidos en el país.
Se supone que las exportaciones son independientes del nivel de ingreso de la economía, por lo
tanto son autónomas; mientras que las importaciones dependen del nivel de actividad de la
economía y son un componente de la oferta agregada de la economía.
La disponibilidad interna de bienes incluye lo que se produce en el país (Y) más los bienes
importados (M = mY), que si bien forman parte de la oferta agregada (OA), no son un
componente del ingreso o producto de la economía. En la ecuación de importaciones observamos
que éstas constituyen una proporción “m” del ingreso, siendo “m” la propensión marginal a
importar y es igual al cociente entre la variación en las importaciones y la variación en el ingreso
(m = ∆ M / ∆ Y), que se interpreta como la variación en las importaciones por cada unidad
monetaria en que varíe el ingreso.
Las exportaciones son un componente de la demanda agregada autónoma de la economía, por lo
tanto un cambio en ellas provoca una variación en el ingreso de equilibrio; mientras que las
importaciones son una filtración más que se agrega a las ya existentes (impuestos + ahorro),
porque parte del ingreso que obtienen las familias será gastado en bienes producidos en el resto
del mundo.
Partiendo de las condiciones que debe cumplir el ingreso para ser de equilibrio, se puede derivar
la fórmula para calcularlo:
Ye = GAo / 1-c (1 – t) + m;
Reemplazando por los valores del ejercicio y suponiendo que los impuestos son sólo autónomos:
Ye= 640 / 1 – 0,80 + 0,10
El GAo aumentó en 300 unidades monetarias, con respecto al caso de economía cerrada, por la
incorporación de las exportaciones autónomas.
Ye = 2.133,33
El valor obtenido es mayor que el correspondiente al caso de una economía cerrada. Esto no
siempre es así ya que, el efecto de la apertura de la economía sobre el ingreso de equilibrio
depende de las exportaciones y de las importaciones, es decir del saldo de la balanza comercial.
Introducción a la Economía I – Cátedra a Distancia
Unidad 9
En este caso las exportaciones superan a las importaciones, es por esta causa que el ingreso de
equilibrio es mayor que en el caso de economía cerrada.
Como ejercitación, puede calcular el ingreso de equilibrio, suponiendo la ecuación impositiva del
apartado f).
Comprobaremos que el ingreso obtenido es de equilibrio, verificando que cumpla con las dos
condiciones conocidas.
O.A = D.Ap
D.Ap = GAo + c Y
D.Ap = 640 + 0,80 . 2.133,33
D.Ap = 2.346,40 u.m.
O.A = Y + 0,10 Y
O.A = 2.133,33 + 0,10 . 2.133,33
O.A = 2.346,66 u.m, valor que difiere insignificativamente
respecto al de la demanda agregada planeada por una cuestión de redondeo en los decimales.
La otra condición que debe cumplir el ingreso de equilibrio,
Filtraciones = Gastos Compensatorios
SF + T + M = Io + Go + Xo (*)
Siendo el ahorro de las familias:
SF = - 140 + 0,20 . 2.133,33
SF
condición de equilibrio (*):
=
286,67; entonces reemplazando en la
286,67 + 200 + 213,33 = 200+ 200 + 300
700 = 700
Verificándose la igualdad. También se puede plantear esta condición como:
Ahorro de la economía = Inversión
El ahorro de la economía comprende el ahorro de las familias, del gobierno y del sector externo,
definiendo a este último como la diferencia entre el valor de las importaciones y el de las
exportaciones. Entonces:
SF + (T – Go) + (M – Xo) = Io
286,67 +
0
-
86,67 = 200 u.m.
Recomendamos que compruebe ambas condiciones de equilibrio para el caso de economía
abierta con impuestos autónomos y proporcionales.
h) ¿Cuál es el valor del multiplicador en los casos de (f), (g) y (f y g)?
Para el caso descripto por el apartado (f) el multiplicador es igual a:
1
-c
k´= ---------------------; en el caso del multiplicador de To; k´ = ---------------------1 – c (1 – t )
1 – c (1 – t)
Introducción a la Economía I – Cátedra a Distancia
Unidad 9
El multiplicador del apartado (h), correspondiente a una economía abierta con impuestos
autónomos:
1
-c
k´= ---------------------; en el caso del multiplicador de To; k´ = ---------------------1–c+m
1–c +m
Finalmente, el multiplicador para una economía abierta con impuestos proporcionales y
autónomos:
1
-c
k´= ---------------------; en el caso del multiplicador de To; k´ = ---------------------1 – c (1 – t ) + m
1 – c (1 – t) + m
¿Podría Ud. Explicar por qué el multiplicador para una economía abierta es menor que el de una
economía cerrada?
i) Verifique por el método de oferta global igual a demanda global el ingreso de (g).
Esta consigna fue respondida en el apartado (g).
Ejercicio 11
a) Ye =
100 + 50 + 200
= 875
1 − 0.8(0.75)
k = 2.5
b) Superávit del Gobierno (SG) = T – G
SG = 0.25(875)-200 = 18.75 ! Como SG> 0, el Gobierno es superavitario.
c)
∆ Ye = k∆ Io
∆ Ye = 2.5 * 50 = 125
Ye' = 875 + 125 = 1000
SG' = 0.25(1000) − 200 = 50
Introducción a la Economía I – Cátedra a Distancia
Unidad 9
Ejercicio 12
∆ Ye = 200
1
=5
1 - 0.8
Aumento del Gasto Público :
k=
200
= 40
5
Reducción de impuestos autónomos :
∆ Ye = k∆ Go ⇒ ∆ Go =
∆ Ye = −c k ∆ To ⇒ ∆ To = −
200
= −50
( −0.8)5
(Política fiscal de gasto expansiva)
(Política fiscal tributaria expansiva)
Aumento del Gasto Público financiado con un incremento en los Impuestos autónomos :
∆Ye = k(∆( o − c∆∆o )
⇒ ∆ Go = ∆ To = 200
donde ∆ Go = ∆ To
(Política fiscal de presupuesto equilibrad o. Es expansiva. )
Todas estas son políticas fiscales, es decir que utilizan instrumentos que el gobierno
puede manejar directamente, por medio de los elementos que componen el
presupuesto público.
Hay otras variables macroeconómicas que pueden cambiar y llevar al ingreso de
equilibrio de su nivel de 1000 al nivel de pleno empleo de 1200, las cuales no pueden
ser directamente controladas por el Gobierno (no son herramientas de política fiscal).
Ellas son:
Aumento en la Inversión autónoma:
200
∆ Ye = k∆ Io ⇒ ∆ Io =
= 40
5
Aumento en el Consumo autónomo:
200
∆ Ye = k∆ Co ⇒ ∆ Co =
= 40
5
Ejercicio 13
∆ Ye = 500
1
k=
= 3.57
1 - 0.8(1 - 0.10)
Aumento del Gasto Público :
500
∆ Ye = k∆ Go ⇒ ∆ Go =
= 140
3.57
Ejercicio 14
El Gobierno quiere reducir el gasto y disminuir los impuestos de manera que ∆ Ye = 0
Entonces:
Reducción del Gasto Público con reducción en los Impuestos autónomos :
∆ Ye = 0 = k(∆ Go − c∆ To )
1
(-100 - 0.8∆ To ) ⇒ −100 = 0.8∆ To ∴ ∆ To = - 125
1 − 0.8
Es decir que deberá reducir los impuestos autónomos en 125.
0=
Introducción a la Economía I – Cátedra a Distancia
Unidad 9
Ejercicio 15
a)
1

(10) = 1.25 * 10 = 12.5
∆Ye =
∆ Go = 10 ⇒ 
1 − 0.4 + 0.2
∆BC = ∆X − ∆M = 0 − 0.2 * 12.5 = −2.5

Es decir, se incrementa el ingreso de equilibrio y se genera un déficit en la balanza
comercial.
b)
1

(-10) = 1.25 * (-10) = −12.5
∆ Ye =
∆ Xo = −10 ⇒ 
1 − 0.4 + 0.2
∆ BC = ∆ X − ∆ M = −10 − 0.2 * (-12.5) = −7.5

Es decir, se reduce el ingreso de equilibrio y se genera un déficit en la balanza
comercial.
c)
1

(-10) = 1.25 * (-10) = −12.5
∆ Ye =
∆I o = −10 ⇒ 
1 − 0.4 + 0.2
∆ BC = ∆ X − ∆ M = 0 - 0.2 * (-12.5) = -2.5

Es decir, se reduce el ingreso de equilibrio y se genera un déficit en la balanza
comercial.
Compare entre los distintos casos planteados y extraiga conclusiones de las diferencias
encontradas.
Ejercicio 16
a)
Ye = 1250
Ype − Ye = 2000 − 1250 = 750
A esta economía le faltan 750 para llegar a su nivel de pleno empleo.
∆ Ye = 750 =
b)
∆ Ye =
1
∆ Io ⇒ ∆ Io = 150
0.2
1
∆ Io = 5 * 150 = 750
0.2
Ye' = 2750
El aumento del ingreso en este caso es también de 750. Pero hay que tener en cuenta
que en este caso la economía se encontraba inicialmente en su nivel de pleno empleo,
por lo que se ha llevado al equilibrio del ingreso
Introducción a la Economía I – Cátedra a Distancia
Unidad 9
Ejercicio 17
a)
Ye =
20 + 50
= 140
1 - 0.5
Y=OA
b) Demanda planeada
D
DA
DA = 20 + 50 + 0.5Y
DA = 70 + 0.5Y
70
Si Y=60
DA = 20 + 50 + 0.5 * 60
DA = 100
60
c)
Hay un exceso de demanda
VE = Y − DA
VE = 60 − 100 = −40
d)
Demanda realizada = 60
Oferta realizada = 60
e)
S = -20+0.5*60 = 10
Io = 50
(Inversión planeada)
VE + Io = -40 + 50 = 10
(Inversión realizada)
S
S, I
50
Io
10
60
140
Y
140
Y
Introducción a la Economía I – Cátedra a Distancia
Unidad 9
f)
Los productores, al observar la desacumulación de stocks no deseada que están
teniendo, reaccionarán incrementando su producción para satisfacer la demanda
excedente.
Ejercicio 18
A
200
200
0.3
300
100
2100
1600
-200
-
C0
I0
S
G
T0
X
m
Ye
C
T-G
X-M
B
200
200
0.3
300
100
170
0.12
1904.76
1463.3
-200
-58.6
C
200
200
0.3
300
300
170
0.12
1571.4
1300
0
-18.6
Ejercicio 19
Una situación de equilibrio en el mercado del producto no se corresponde
necesariamente con el pleno empleo. Este caso se muestra en la siguiente figura, en la
que se muestra el caso en que existe desempleo:
Y=OA
D
DA
GA
Ye
Ype
Y
Para llevar el nivel de equilibrio del ingreso hacia su valor de pleno empleo, el Gobierno
puede alterar cualquiera de los instrumentos que tiene a su alcance, sea el Gasto
Público, los Impuestos autónomos o la alícuota impositiva proporcional al ingreso. En
los dos últimos casos el Gobierno debería reducir el valor de esas variables (reducir To
o t), si lo que desea es aumentar el valor del ingreso de equilibrio, o bien debería
aumentar el nivel de Go bajo ese mismo propósito. En este modelo estas medidas son
siempre efectivas para lograr el objetivo de pleno empleo.
Introducción a la Economía I – Cátedra a Distancia
Unidad 9
Ejercicio 20
El multiplicador en una economía cerrada y sin gobierno queda expresado de la
siguiente manera:
k=
1
(1)
1− c
a) En una economía con una alta PMgC este multiplicador tenderá a ser alto. ¿Cómo
se explica este resultado en términos económicos?.
Imaginemos dos casos
extremos. El primero en el que la PMgC sea cercana a 0 y otro caso en el que la
PMgC sea cercana a 1. Supongamos también que aumenta en 1 unidad el Gasto
autónomo de la economía y por lo tanto la demanda agregada también se
incrementa en 1 unidad. Esto genera un desajuste en la economía, por lo que los
productores deberán cubrir esta demanda excedente incrementando la oferta de la
economía. En un primer momento el ingreso aumentará en la misma magnitud en
que ha aumentado el Gasto Autónomo (=1). La Familias verán entonces
incrementado su ingreso en una unidad.
•
•
Si consideramos el primer caso extremo (c ≅ 0), las familias decidirán ahorrar todo
el ingreso adicional. Por lo tanto el consumo, y por ende la demanda agregada no
se verán alterados. De este modo la economía retorna al equilibrio. El incremento
en el gasto autónomo no ha tenido efectos propagadores sobre la economía dado
que las familias ahorran todo su ingreso adicional. El multiplicador de la economía
es entonces bajo, en este caso cercano a uno, como puede deducirse de la
ecuación (1).
Si consideramos el segundo caso extremo (c ≅ 1), ante el aumento en 1 unidad de
su ingreso las familias decidirán gastar todo este ingreso adicional. Por lo tanto
incrementarán su consumo en una unidad, elevándose consecuentemente la
demanda agregada de la economía. Este nuevo exceso de demanda deberá ser
cubierto por los productores. Esto llevará a un nuevo incremento en el ingreso de la
economía, en el consumo (dado que las familias consumen todo su ingreso
adicional) y en la demanda agregada, generándose nuevamente un exceso de
demanda. Este proceso continuará, bajo los supuestos del modelo, y el ingreso se
seguirá expandiendo. El incremento inicial del gasto autónomo ha tenido efectos
propagadores sobre la economía que se mantienen en el tiempo. En efecto,
podemos deducir de la ecuación (1) para una PMgC cercana a 1, el multiplicador
adoptará un valor alto, tendiendo a infinito cuando sea igual a 1.
b) El multiplicador adoptará valores cercanos a 1 (la explicación es la misma que la
del inciso a), el primer caso extremo).
Introducción a la Economía I – Cátedra a Distancia
Unidad 9