Se trata de refrentar un disco macizo de 300 mm de diámetro en un
Anuncio

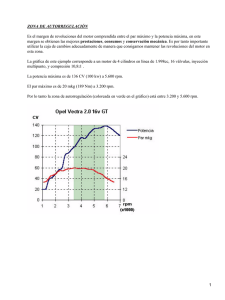
Universidad de Navarra Nafarroako Unibertsitatea Escuela Superior de Ingenieros Ingeniarien Goi Mailako Eskola ASIGNATURA GAIA: TECNOLOGÍAS DE FABRICACIÓN TIEMPO: 1.5 HORA CURSO KURTSOA: 5º FECHA DATA: 19.09.01 P1_SEP_01 Se trata de refrentar un disco macizo de 300 mm de diámetro en un torno CNC. La característica PN correspondiente al motor del husillo principal (cabezal) aparece en la figura. Su rendimiento es del 80%. La profundidad de pasada de la operación es de 10 mm y la presión específica de la pieza es de 2500 N/mm2. Se pide: 1) El avance por vuelta, sabiendo que se mantiene constante durante el refrentado, y el tiempo de la operación (tomar creces nulas). Además de la potencia, el proceso está sujeto a las siguientes restricciones: • • • Se trabajará a velocidad de corte constante de 130 m/min, siempre que sea posible. El tiempo de refrentado debe ser mínimo. La rugosidad media Ra debe ser menor que 5 µm. Se dispone de cuchillas con radios de punta r (0.4, 0.8, 1.2, 2.4) mm. El torno tiene una gama continua de velocidades de avance entre 0 y 2000 mm/min. 2) Dibujar un esquema en el que se representen las gráficas: VC-r, PC-r, N-r, Zw-r y Vf-r correspondientes a la operación siendo r el radio actual de la pieza (0≤ r ≤ 150 mm). 3) Los ángulos de la herramienta son: Kr=90º, K´r=5º, γf=5º y αf=5º. a) Decir a partir de qué diámetro talonaría el filo principal. b) Ilustrar la respuesta con un esquema claro en el que se representen la interacción entre la herramienta y la pieza. Potencia del motor del husillo principal 30 25 P (kW) 20 15 10 5 0 0 200 400 600 800 1000 N (rpm) Puntuación: 1): 1.5, 2): 0.5, 3):0.5 Resolución 1200 1400 1600 1800 2000 Como el refrentado es hasta el centro (d=0) no va a ser posible hacerlo todo a VC constante. Habrá dos tramos: Tramo 1: Desde ∅300 mm hasta ∅d* VC 130 ⋅10 3 mm / min ∗ siendo d = = = 20.7 mm π ⋅ N MÁX π ⋅ 2000 rpm Tramo 2: Desde ∅20.7 mm hasta el centro. El tiempo de operación se expresa como: t op = t 1 + t 2 Cálculo de t1: En el cálculo del tiempo correspondiente al primer tramo, como la velocidad de giro N es variable y af, constante, la velocidad de avance VX es variable. Por tanto, la expresión del tiempo de operación en el primer tramo se expresa como: dt 1 = − dr dr =− =− VX af ⋅ N 2π dr (− r ⋅ dr ) = VC a f ⋅ VC af ⋅ 2πr Integrando entre D=300 mm y d=20.7 mm, queda: t1 = 2π a f ⋅ VC d∗ 2 D 2 ∫ D 2π r 2 2 − r ⋅ dr = a f ⋅ VC 2 d∗ 2 Cálculo de t2: en esta zona, 0 ≤ r ≤ 20.7 mm , y como N=2000 rpm y af, constante, la velocidad de avance también es constante. Por tanto, d∗ t2 = 2 af ⋅ N El tiempo de operación top será mínimo cuando t1 y t2 lo sean, y como sólo dependen de af, top será mínimo cuando af sea máximo. Cálculo del valor de af compatible con las restricciones. • Restricción de rugosidad: a 2 Ra = f a f = 32 ⋅ r ⋅ R a 32 ⋅ r Para que af sea máximo, r debe serlo también. Por ello, se toma r=2.4 mm. Como Ra<5µm, entonces, • a f < 32 ⋅ 2.4 mm ⋅ 5 ⋅ 10 −3 mm = 0.62 mm Restricción de potencia de corte PC PC = p S ⋅ A C ⋅ VC La potencia de corte máxima se dará durante el tramo 1 ya que durante el tramo 2, VC< 130 m/min y los demás parámetros son iguales. Además para D=300 mm, la velocidad de giro es: N = 130 ⋅ 10 3 mm / min = 137.93 rpm π ⋅ 300 mm y para N< 200 rpm, la potencia disponible es menor de 25x0.8 kW. En consecuencia, para D=300 mm: • • La potencia necesaria es máxima. La potencia disponible es mínima. Por tanto, si la máquina puede comenzar la operación en D=300 mm, la terminará sin problemas de potencia. Así, se estudia la potencia necesaria en D=300 mm y compararla con la potencia disponible. Potencia disponible a 137.9 rpm Pdisp = 0.8 ⋅ 25 ⋅ 137.9 = 13.79 kW 200 N m 1 min ⋅ a mm ⋅ 10 mm ⋅ 130 = 54167 ⋅ a f ( W ) f min 60 s mm 2 Por tanto, 54167 ⋅ a f ≤ 13.79 ⋅10 3 de donde, a f ≤ 0.255 mm , que es más restrictiva que el debido a Potencia de corte: PC = 2500 la Ra. • Restricción de VX: VX = a f ⋅ N Tramo 2: N=2000 rpm → VX = 0.255 mm ⋅ 2000 rpm = 510 mm , que está dentro de la gama de min velocidades de avance disponibles en la máquina. Tramo 1: La velocidad de avance varía desde 510 mm/min para d*=20.7 mm hasta VX=0.255·137,93=35.17 mm/min para D=300 mm, que también está dentro de la gama. Por tanto: a f = 0.255 mm . Sustituyendo en las expresiones anteriores: 300 2 20.7 2 π 2 t1 = − mm = 2.12 min mm ⋅ 0.255 mm 2 2 130 ⋅ 10 3 min 20.7 2 t2 = = 0.02 min 0.255 ⋅ 2000 El tiempo de operación vale: t op = 2.14 min 2) 140 350 130 m/min 100 250 Zw (cm /min) 300 Vc (m/min) 120 200 3 80 331 cm3/min 60 150 40 100 20 50 0 0 0 10.35 30 60 90 120 0 10.35 150 30 60 90 120 150 Radio (mm) Radio (mm) 600 16 13.79 kW 14 500 400 10 Vf (mm/min) Potencia (kW) 12 8 6 300 200 4 100 2 34.5 mm/min 0 0 0 10.35 30 60 90 120 150 0 10.35 30 60 90 120 Radio (mm) Radio (mm) 2500 N (rpm) 2000 1500 1000 500 137.93 rpm 0 0 10.35 30 60 90 120 150 Radio (mm) 3) Si η=α, la herramienta talona. γ = 5º HERRAMIENTA η α=5º η VC=πdN tag η = Vf a ⋅N a = f = f = tag 5º VC π ⋅ d ⋅ N π ⋅ d Vf El diámetro a partir del cual la herramienta talona es: d = 0.25 = 0.91 mm π ⋅ tag 5º 150