Integración Aproximada

1
Integración Aproximada
Método del Rectángulo
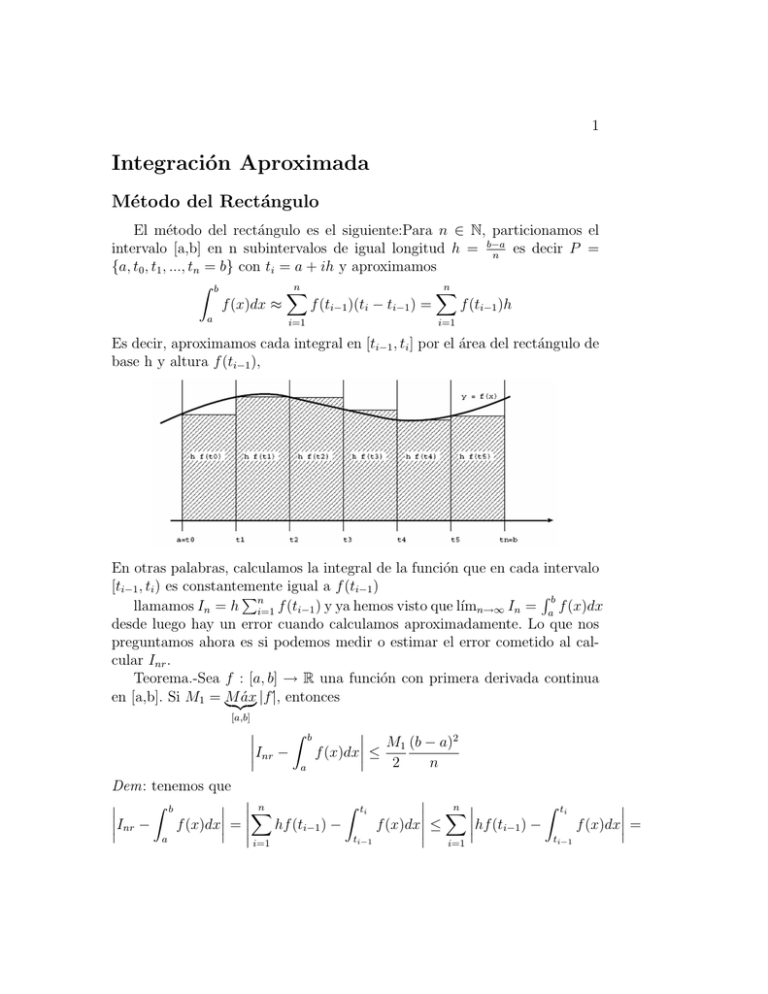
El método del rectángulo es el siguiente:Para n ∈ N, particionamos el
intervalo [a,b] en n subintervalos de igual longitud h = b−a
es decir P =
n
{a, t0 , t1 , ..., tn = b} con ti = a + ih y aproximamos
Z b
n
n
X
X
f (x)dx ≈
f (ti−1 )(ti − ti−1 ) =
f (ti−1 )h
a
i=1
i=1
Es decir, aproximamos cada integral en [ti−1 , ti ] por el área del rectángulo de
base h y altura f (ti−1 ),
En otras palabras, calculamos la integral de la función que en cada intervalo
[ti−1 , ti ) es constantemente igual a f (ti−1 )
Rb
P
llamamos In = h ni=1 f (ti−1 ) y ya hemos visto que lı́mn→∞ In = a f (x)dx
desde luego hay un error cuando calculamos aproximadamente. Lo que nos
preguntamos ahora es si podemos medir o estimar el error cometido al calcular Inr .
Teorema.-Sea f : [a, b] → R una función con primera derivada continua
en [a,b]. Si M1 = M
| {záx} |f´|, entonces
[a,b]
Z b
M1 (b − a)2
Inr −
≤
f
(x)dx
2
n
a
Dem: tenemos que
n
Z b
Z ti
Z ti
n X
X
Inr −
=
hf (ti−1 ) −
=
f
(x)dx
hf
(t
)
−
f
(x)dx
≤
f
(x)dx
i−1
a
ti−1
ti−1
i=1
i=1
2
n Z
X
i=1
ti
ti
Z
f (ti−1 )dx −
ti−1
ti−1
n Z
X
n Z
X
f (x)dx =
i=1
ti
ti−1
(f (ti−1 ) − f (x))dx ≤
ti
|f (ti−1 ) − f (x)| dx
ti−1
i=1
Por el teorema fundamental del cálculo
Z
x
f (x) − f (ti−1 ) =
f 0 (t)dt
ti−1
por lo tanto
Z
|f (x) − f (ti−1 )| dx ≤
ti
Z
M1 (x − ti−1 ) dx = M1
| {z }
ti−1
u=x−ti−1
du=dx
Por tanto
Z b
n Z
X
Inr −
f (x)dx ≤
a
i=1
udu = M1
0
|{z}
u2 h
h2
|0 = M1
2
2
x=ti−1 ⇒u=0
x=ti ⇒u=h
ti
|f (ti−1 ) − f (x)| dx ≤
ti−1
h
n
X
i=1
M1
h2
h2
= nM1 =
2
2
(b − a)2
M1 (b − a)2
=
2n2
2
n
Observación. Si conocemos una cota para M1 , entonces podemos saber cuál
es el valor de n que debe tomarse para calcular la integral aproximada con
un error dado.
R2
2
Ejemplo 1. Supongamos que queremos calcular aproximadamente 0 e−x dx
con un error menor a 0.1
2
2
tenemos que f (x) = e−x por tanto f 0 (x) = −2xe−x y deducimos que
|f 0 (x)| ≤ 4 para x ∈ [0, 2] por tanto para n ∈ (N )
Z 2
4 22
8
2
−x
Inr −
≤
e
dx
2n =n
0
nM1
y para asegurar un valor < 0,1
8
8
< 0,1 ⇒
< n ⇒ 80 < n
n
0,1
Para n=80 la fórmula nos da Inr = 0,89435
3
Método del Trapecio
La regla del trapecio es la siguiente: Para n ∈ N particionamos (de la
misma manera que antes)P = {a = to , t1 , ..., tn = b} con ti = a + ih y
aproximamos
Z
b
f (x)dx ≈ Int =
a
n
X
f (ti−1 ) + f (ti )
i=1
2
(ti − ti−1 )
Es decir, aproximamos cada integral en [ti−1 , ti ] por el área del trapecio de
altura h y bases f (ti−1 ) y f (ti )
En otras palabras, calculamos la integral de la función que en cada intervalo
[ti−1 , ti ) es lineal y coincide con f en ti−1 y en ti
Teorema (Estimación del error de la regla del trapecio). Sea f : [a, b] → R
una función con segunda derivada continua en [a,b]. Si M2 = M áx[a,b] |f 00 |,
entonces
Z b
3
Int −
≤ M2 (b − a)
f
(x)dx
n2
a
Dem Tenemos que
n
Z b
Z
X f (ti−1 ) + f (ti )
Int −
f (x)dx = h
−
2
a
=
Z ti
n X
f (ti−1 ) + f (ti )
f (x)dx ≤
−
f
(x)dx
h
2
ti−1
ti−1
i=1
n Z ti
X
i=1
ti−1
ti
i=1
ti
dx −
f (x)dx
ti−1
(f (ti−1 ,f (ti ))
Z
Li
f uncion
lineal
L (x)
| i{z }
que
pasa
por
4
n Z
X
=
i=1
ti
ti−1
n Z
X
Li (x) − f (x)dx ≤
i=1
ti
|Li (x) − f (x)| dx
ti−1
Intentemos ahora acotar cada uno de estos términos. Para ello consideremos
un intervalo [ti−1 , ti ] de la partición, y definamos la función g(x) = Li (x) −
f (x) , que se anula en x = ti−1 y en x = ti y por el teorema de Rolle existe
ξi ∈ (ti−1 , ti ) tal que g 0 (ξi ) = L0i (ξi ) − f 0 (ξi ) = 0. El teorema fundamental del
cálculo nos dice que si x ∈ (ti−1 , ti ), entonces
Z x
Z x
00
0
0
g 00 (t)dt
g (t)dt =
g (x) = g (ξi ) +
ξi
ξi
como Li es lineal, g 00 (t) = L00i (t) − f 00 (t) = −f 00 (t) para t ∈ (ti−1 , ti ). por lo
tanto
Z x
Z x
0
00
00
|g (x)| = g (t)dt = f (t)dt ≤ |x − ξi | M2 ≤ hM2
ξi
ξi
Esto implica que para s ∈ (ti−1 , ti )
Z s
Z s
0
|g(s)| = |g(s) − g(ti − 1)| = g (x)dx ≤
|g 0 (s)| dx ≤ M2 h(s−ti−1 ) ≤ M2 h2
ti
ti
finalmente por lo anterior y del hecho de que g(x) = Li (x) − f (x) se sigue
que
Z ti
Z ti
|g(x)| dx ≤ M2 h2 h = M2 h3
|Li (x) − f (x)| dx =
ti−1
ti−1
concluimos entonces que
Z b
ti Z
X
Int −
f (x)dx ≤
a
ti−1
ti
ti−1
|Li (x) − f (x)| dx ≤ nM2 h3 = M2 n
(b − a)3
(b − a)3
=
M
2
n3
n2