7 – ANTITRASLACIÓN 7.1 – DEFINICIÓN Dada una recta e y dos

UNIDAD 2
CONCEPTOS REQUERIDOS –2b
7 – ANTITRASLACIÓN
7.1 – DEFINICIÓN
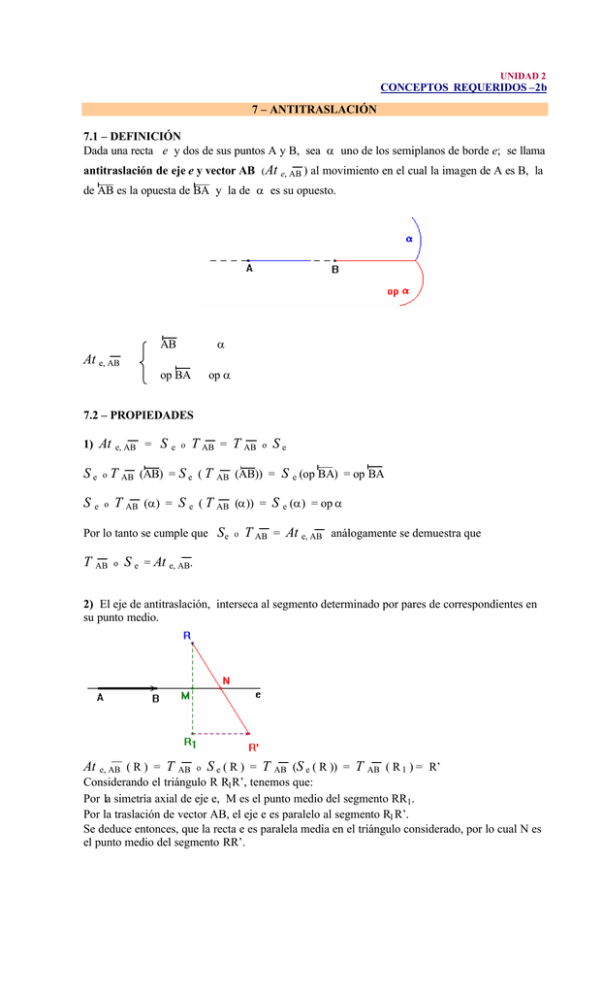
Dada una recta e y dos de sus puntos A y B, sea α uno de los semiplanos de borde e; se llama
antitraslación de eje e y vector AB ( At e, AB ) al movimiento en el cual la imagen de A es B, la
de AB es la opuesta de BA y la de α es su opuesto.
α
AB
At e, AB
op α
op BA
7.2 – PROPIEDADES
1) At
e, AB
= S
e o
T AB = T AB
o
Se
S e o T AB (AB) = S e ( T AB (AB)) = S e (op BA) = op BA
Se
o
T AB (α) = S e ( T AB (α)) = S e (α) = op α
Por lo tanto se cumple que S e
T AB
o
o
T AB = At e, AB análogamente se demuestra que
S e = At e, AB.
2) El eje de antitraslación, interseca al segmento determinado por pares de correspondientes en
su punto medio.
At e, AB ( R ) = T AB
o
S e ( R ) = T AB (S e ( R )) = T AB ( R 1 ) = R’
Considerando el triángulo R R1R’, tenemos que:
Por la simetría axial de eje e, M es el punto medio del segmento RR1.
Por la traslación de vector AB, el eje e es paralelo al segmento R1 R’.
Se deduce entonces, que la recta e es paralela media en el triángulo considerado, por lo cual N es
el punto medio del segmento RR’.
3) El eje de antitraslación, es paralelo a la bisectriz del ángulo que determinan dos semiplanos
correspondientes, de borde no paralelo al eje.
En la figura adjunta se ha construido las imágenes de la recta r y del semiplano ω en At e, AB.
La semirrecta Qz es la bisectriz del ángulo ω ∩ ω’.
Para demostrar que el eje e es paralelo a la semirrecta Qz, justificaremos que los ángulos α y β
son congruentes.
At e, AB (β) = β’
⇒ β =c β’
Por ser opuestos por el vértice, los ángulos OO’Q y β’ son congruentes, por lo cual también lo
son los ángulos OO’Q y β.
El ángulo ω ∩ ω’ es externo en el triángulo OO’Q por lo que es igual a la suma de OO’Q y β o
sea que ω ∩ ω’ =c 2β.
La semirrecta Qz es la bisectriz del ángulo ω ∩ ω’, entonces ω ∩ ω’ = 2α.
De las dos últimas relaciones obtenidas se deduce que 2α =c 2β y por lo tanto que α =c β.
8 – TEOREMA FUNDAMENTAL DE LAS ISOMETRÍAS.
Las únicas isometrías del plano son: la identidad, las simetrías axiales, las simetrías
centrales, las traslaciones, las rotaciones y las antitraslaciones.
Recordemos que el axioma de Determinación de las isometrías dice:
Dados dos puntos O y O’, dos semirrectas con origenes en ellos Os y O’s’ y dos semiplanos
de borde dichas semirrectas α y β, existe y es única la isometría M tal que:
M(O) = O’
M(Os) = O’s’
M(α) = β
Teniendo en cuenta este axioma, si consideramos dos semirrectas Os y O's', cualquiera sea
su posición siempre existen dos isometrías, una directa y otra indirecta que hacen corresponder
Os con O's'. Utilizando las propiedades estudiadas, comprobaremos que para las distintas
posiciones que pueden ocupar estas 2 semirrectas, las dos isometrías que transforman la 1ª en la
2ª son dos de las antes mencionadas.
Encontraremos en cada caso dos isometrías, una directa y otra indirecta, en las cuales la
imagen de la semirrecta Os sea la O's':
1) Os = O's'
Isometría directa:
contenida en x
I
Isometría indirecta: S x
2) O's' = op Os
Isometría directa:
contenidas en x
CO
Isometría indirecta: S r
r es la perpendicular a x en O.
3) O's' ⊂ Os
Isometría directa:
T OO’
At x, OO’
Isometría indirecta:
4) Os y O's'
Isometría directa:
contenidas en x
contenidas en x
CM
M es el punto medio del segmento OO’.
Isometría indirecta: S z
z es la mediatriz del segmento OO’.
5) x || y
OO' ⊥ x
Isometría directa:
T OO’
Isometría indirecta: S z
z es la mediatriz del segmento OO’.
6) x || y
OO' ⊥ x
Isometría directa: C M
M es el punto medio del segmento OO’.
Isometría indirecta:
At OO’, OO’
7) x || y
Isometría directa:
T OO’
Isometría indirecta: At m, PO’
m es la paralela media entre x e y y P la proyección ortogonal de O sobre y.
8) x || y
Isometría directa: C M
M es el punto medio del segmento OO’.
Isometría indirecta:
At r, OP
r es la perpendicular a x por M y P la proyección ortogonal de O sobre y.
9) x ∩ y = { Q } x e y forman ángulos α y β. OQ = O'Q
Isometría directa:
R Q, – α
Isometría indirecta: S z
z es la mediatriz del segmento OO’.
10) x ∩ y = { Q } x e y forman ángulos α y β. OQ ≠ O'Q
Isometría directa: R C, α
El punto C es la intersección de la mediatriz del segmento OO’ con la bisectriz del ángulo β.
Observación:
β es el ángulo determinado por dos semiplanos correspondientes y α el determinado por un
semiplano y el opuesto de su imagen.
También se puede determinar el centro de rotación con este procedimiento:
Elegir un punto P en la semirrecta Os, hallar su imagen P’, que pertenecerá a la semirrecta O’s’
de modo que d(O’, P’) = d(O,P) y lue go construir C como punto de intersección de las
mediatrices de los segmentos OO’ y PP’.
Isometría indirecta: At e, SO’
El eje e es la paralela a la bisectriz del ángulo α por el punto medio del segmento OO’ y S es el
simétrico de O respecto a e.
Se trazó la bisectriz del ángulo α, puesto que este ángulo está determinado por un semiplano y su
correspondiente en la antitraslación.
Otra forma de construir el eje de antitraslación:
Elegir un punto P en la semirrecta Os, hallar su imagen P’, que pertenecerá a la semirrecta O’s’
de modo que d(O’, P’) = d(O,P) y determinar el eje con los puntos medios de los segmentos
OO’ y PP’.
9 – COMPOSICIÓN DE ISOMETRÍAS
9.1 – COMPOSICIÓN DE
DOS SIMETRÍAS AXIALES
1) Ejes coincidentes
a= b
Sb
o
Sa =
I
2) Ejes disjuntos
3) Ejes secantes
a∩ b=φ
a∩b={O}
T 2OP
El producto de dos simetrías axiales de ejes
paralelos disjuntos, es la traslación cuyo
vector tiene dirección perpendicular a la de los
ejes, sentido del primer al segundo eje y
módulo igual al doble de la distancia entre
ellos.
R O, +2α =
El producto de dos simetrías axiales de ejes
secantes, es la rotación cuyo centro es el
punto de intersección de los ejes, el ángulo es
el doble del que ellos forman y el sentido, el
que va del primer al segundo eje en el ángulo
considerado
R O, – 2β
4) Ejes perpendiculares a ⊥ b
El producto de dos simetrías axiales de ejes
coincidentes, es la identidad.
CO
El producto de dos simetrías axiales de ejes
perpendiculares, es la simetría central con
centro en el punto de corte de ambos ejes.
JUSTIFICACIONES.
En los cuatro casos considerados la composición debe ser una isometría directa.
1) La simetría axial es un movimiento involutivo. Propiedad de la simetría axial.
2) Veamos cual es la imagen de la semirrecta OP:
S b o S a (OP) = S b (S a (OP)) = S b (op OP) = op O’O
Observando que OP = OO’ resulta que S b o S a es la isometría directa en la cual la imagen de la
semirrecta OO’ es la opuesta de O’O, por lo tanto es la traslación de vector OO’, que es lo
mismo que decir de vector 2OP.
3) Consideremos la semirrecta Ox contenida en la recta a.
S b o S a (Ox) = S b (S a (Ox)) = S b (Ox) = Oy
S b o S a es la isometría directa en la cual la imagen de la semirrecta Ox es Oy tal que el ángulo
xOy mide α + α’ = 2α, por lo tanto es la rotación de centro O, ángulo 2α y sentido antihorario.
4) Es un caso particular del anterior considerando α = 90º.
9.2 – COMPOSICIÓN DE
DOS TRASLACIONES
T CD o TAB =
T AB+CD
El producto de dos traslaciones, es la
traslación cuyo vector es la suma de los
vectores de aquellas.
JUSTIFICACIÓN.
Se trata de la composición de dos movimientos directos, por lo cual el producto también será un
movimiento directo.
Efectuada la suma de los vectores AB y CD, consideramos la semirrecta AS. Su imagen en TAB
será una semirrecta Bx de igual dirección y sentido que AS.
En TCD la imagen de Bx será una semirrecta de origen S que tendrá igual dirección y sentido que
Bx y por lo anterior, que AS. Resulta entonces que TCD (Bx) = op SA.
Resumiendo:
T CD o TAB (AS) = T CD (TAB (AS)) = T CD (Bx) = op SA.
T CD o TAB es la isometría directa en la cual la imagen de la semirrecta AS es la semirrecta
opuesta de SA, por lo tanto T CD o TAB = TAS = TAB + CD .
9.3 – DESCOMPOSICIÓN DE
UNA ANTITRASLACIÓN
At
e, AB =
TAB o S e =
S e o TAB =
C O oS x
S y o CQ
La antitraslación de eje e y vector AB es el
producto de la simetría axial de eje e por la
traslación de vector AB. Este producto es
conmutativo.
La antitraslación de eje e y vector AB es el
producto de la simetría central de centro O por
la simetría axial de eje x. Siendo O un punto
de e, x perpendicular a e y la distancia de O
al eje x es la mitad del módulo del vector.
La antitraslación de eje e y vector AB es el
producto de la simetría axial de eje y por la
simetría central de centro Q. Siendo y perpendicular a e, Q un punto de e, y la distancia
de y a Q es la mitad del módulo del vector.
JUSTIFICACIONES.
Surgen de la primera propiedad de antitraslación y de estudiado en los ítemes anteriores.