En la figura, el plano inclinado un ángulo no tiene

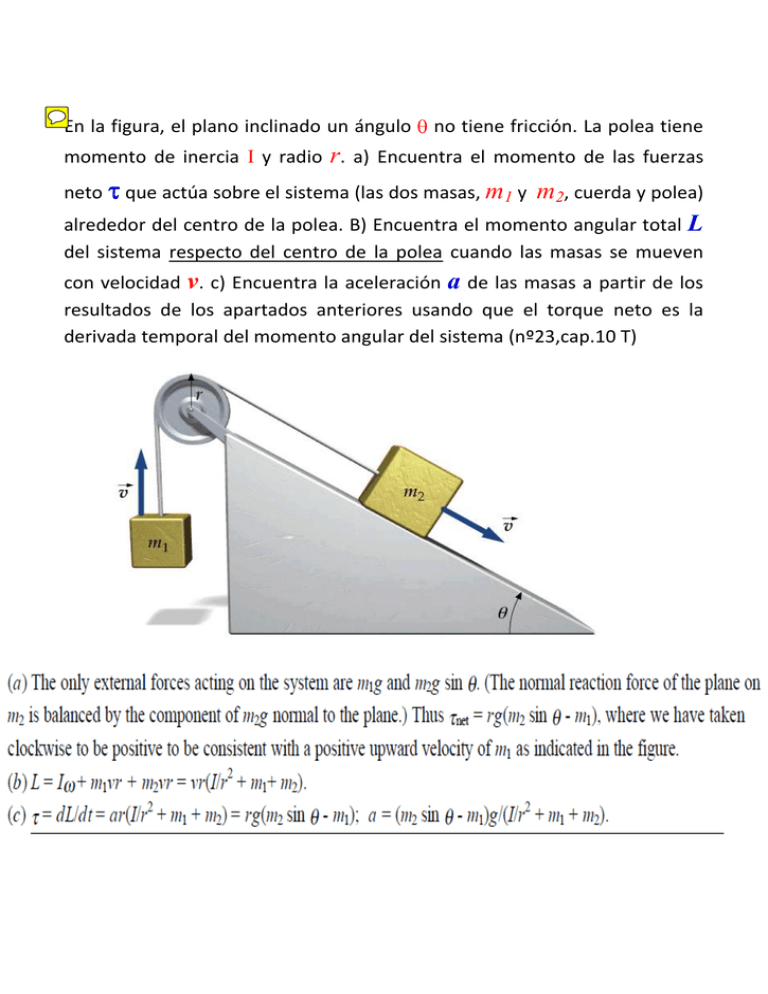
En la figura, el plano inclinado un ángulo
no tiene fricción. La polea tiene
momento de inercia I y radio r. a) Encuentra el momento de las fuerzas
m2, cuerda y polea)
alrededor del centro de la polea. B) Encuentra el momento angular total L
neto
que actúa sobre el sistema (las dos masas, m1 y
del sistema respecto del centro de la polea cuando las masas se mueven
con velocidad v. c) Encuentra la aceleración a de las masas a partir de los
resultados de los apartados anteriores usando que el torque neto es la
derivada temporal del momento angular del sistema (nº23,cap.10 T)
La figura muestra una
varilla de longitud L y
masa M y una bolita de
masilla de masa m. El
sistema se apoya en una
mesa
horizontal
sin
rozamiento. La bolita se
mueve a la derecha con
velocidad v, golpea la
varilla a distancia d del CM
y se queda pegada a ella
en ese punto. Encuentra la
velocidad del CM del sistema y la velocidad angular del sistema respecto del
CM. (nº50,cap.10 T)
2.- Una barra homogénea de longitud L y masa m está sujeta a una pared mediante una
articulación sin rozamiento (en el punto O) y una cuerda sujeta en su extremo (ver figura).
Determinar:
a) Dibujar las fuerzas que actúan sobre la barra y expresar
las ecuaciones para que el sistema esté en equilibrio.
b) Las componentes de la reacción en la articulación y la
tensión de la cuerda.
En un determinado momento se corta la cuerda:
c) Determinar la aceleración angular de la barra justo en el
momento de cortar la cuerda.
d) Utilizando razonamientos energéticos, determinar la velocidad angular de la barra
cuando llega a la posición vertical.
Datos: I0 = 30º, E = 45º, g = 10 ms-2, L = 4 m, m= 50 kg ; ICM = (1/12) m L2.
a) b)
c)
d)
2.- Un listón homogéneo de longitud L = 2 m y masa m = 1 kg está clavado en
la pared por su punto medio (O), de forma que puede girar libremente en torno
a ese punto. Sobre él se aplican las fuerzas F1 = F2 = 4 N y F3 = 6 N, según la
figura.
Dato: I CM = (1/12) m L2
a) Determinar el valor de d para que el listón esté en equilibrio estático, así
como el valor de la normal en el punto O.
b) Si se duplica el módulo de F3 y d = 0.75 m, determinar la aceleración
angular Į del listón en función del ángulo ș que barre, suponiendo que
las fuerzas son siempre verticales.
3.- El sistema de la figura está formado por dos masas m1 y m2 unidas por una cuerda
inextensible mediante una polea de masa M y radio R. Entre m1 y el plano inclinado el
coeficiente de rozamiento cinético es P y entre el plano horizontal y m2 no hay rozamiento.
Inicialmente el sistema se encuentra en reposo y se suelta, moviéndose como se indica
en la figura.
a) Para cada elemento del sistema dibujar
las fuerzas que actúan y expresar las
ecuaciones del movimiento.
b) Calcular la aceleración de los bloques y
las tensiones en la cuerda.
c) Cuando los bloques llevan una
velocidad de v = 0.6 m/s, calcular el
momento angular de la polea con
respecto al CM, su energía de rotación
y la energía total del sistema.
Datos: m1 = 5 kg ; m2 = 0.3 kg ; E = 30o ; P = 0.2 ; M = 2 kg ; R = 0.3 m ; Momento de
inercia de la polea I CM = (1/2) MR2 . Tomar g = 10 m/s2
a)
b)
c)
1.- Una esfera homogénea de masa m y radio R rueda sin deslizar por un plano inclinado
con un ángulo ȕ.Datos: ȕ = 30o; m = 0.5 kg; R = 15 cm; L = 2.5 m; ICM =(2/5) mR 2.
Tomar g = 10 m/s2
a) Dibujar las fuerzas que actúan sobre la esfera y
expresar las ecuaciones de la dinámica de rotación y
de traslación.
b) Calcular la aceleración del centro de masas, la
aceleración angular con respecto al centro de masas
y la fuerza de rozamiento.
c) Si inicialmente se encontraba en reposo, calcular la
velocidad del CM y la velocidad angular de rotación
cuando ha rodado por el plano una longitud L.
a)
b)
c)