1 TEMA 2.- LA CAPITALIZACIÓN COMPUESTA. ( )

TEMA 2.- LA CAPITALIZACIÓN COMPUESTA.
Objetivo: Formalizar la ley de capitalización compuesta y estudiar sus magnitudes derivadas.
1. EXPRESIÓN ANALÍTICA Y REPRESENTACIÓN GRÁFICA.
La ley financiera de capitalización compuesta tiene la siguiente expresión analítica:
L(t; t n ) = (1 + i) t n − t = e k (t n − t ) , con i > 0, y k > 0 , de forma que: k = loge (1+i)= ln(1+i)
[1.]
Las expresiones anteriores pueden escribirse como función de n ( n ∈ R ) , siendo n=tn –t; así:
L(n) = (1+i)n = ek n
[2.]
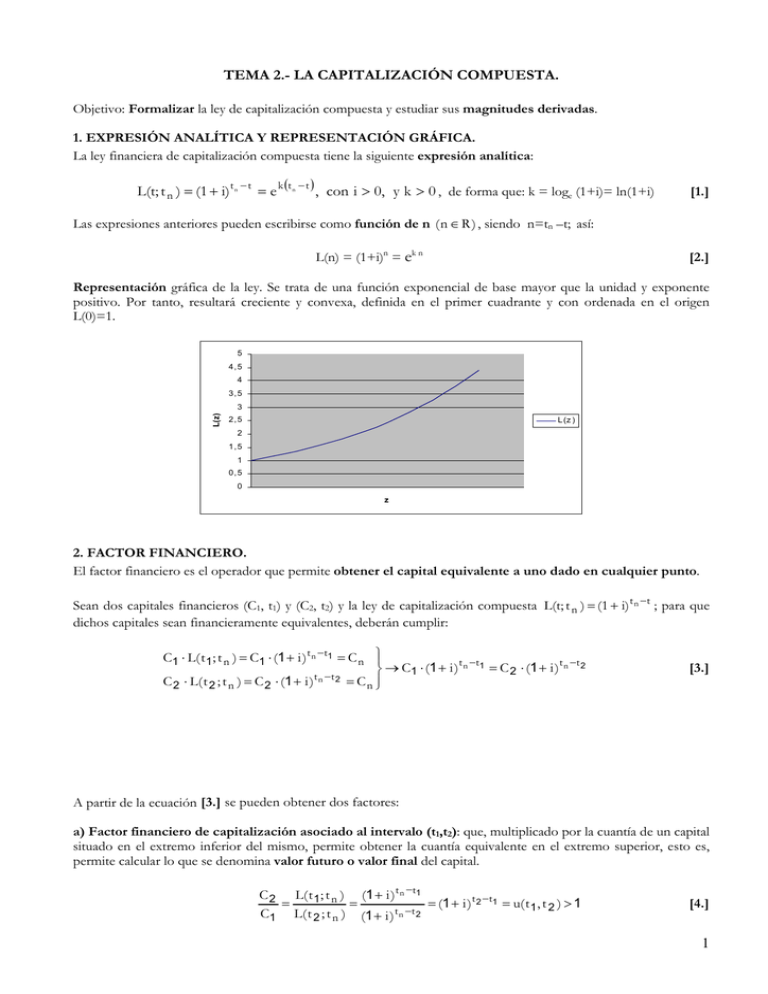
Representación gráfica de la ley. Se trata de una función exponencial de base mayor que la unidad y exponente
positivo. Por tanto, resultará creciente y convexa, definida en el primer cuadrante y con ordenada en el origen
L(0)=1.
5
4,5
4
3,5
L(z)
3
2,5
L (z )
2
1,5
1
0,5
0
z
2. FACTOR FINANCIERO.
El factor financiero es el operador que permite obtener el capital equivalente a uno dado en cualquier punto.
Sean dos capitales financieros (C1, t1) y (C2, t2) y la ley de capitalización compuesta L(t; t n ) = (1 + i) t n −t ; para que
dichos capitales sean financieramente equivalentes, deberán cumplir:
C1 ⋅ L( t 1; t n ) = C1 ⋅ (1 + i ) t n −t1 = C n 
t −t
t −t
 → C1 ⋅ (1 + i ) n 1 = C 2 ⋅ (1 + i ) n 2
t n −t 2
C 2 ⋅ L( t 2 ; t n ) = C 2 ⋅ (1 + i )
= C n 
[3.]
A partir de la ecuación [3.] se pueden obtener dos factores:
a) Factor financiero de capitalización asociado al intervalo (t1,t2): que, multiplicado por la cuantía de un capital
situado en el extremo inferior del mismo, permite obtener la cuantía equivalente en el extremo superior, esto es,
permite calcular lo que se denomina valor futuro o valor final del capital.
C 2 L( t 1; t n ) (1 + i ) t n −t1
=
=
= (1 + i ) t 2 −t1 = u( t 1 , t 2 ) > 1
C1 L( t 2 ; t n ) (1 + i ) t n −t 2
[4.]
1
de forma que:
C 2 = C1 ⋅ u( t 1 , t 2 ) = C1 ⋅ (1 + i ) t 2−t1
[5.]
Si se considera una cuantía unitaria, el factor de capitalización puede interpretarse como la cuantía equivalente en t2
a una unidad de cuantía situada en t1.
En el caso de la capitalización compuesta la expresión del factor de capitalización coincide con la de la ley.
Sin embargo, esto no sucede cuando se trabaja con otras leyes.
b) Factor financiero de actualización, o contracapitalización, asociado al intervalo (t1,t2): que, multiplicado
por la cuantía de un capital situado en el extremo superior del mismo, permite obtener la cuantía equivalente en el
extremo inferior, o lo que se denomina valor actual o valor inicial.
C1 L( t 2 ; t n ) (1 + i ) t n −t 2
=
=
= (1 + i ) t1−t 2 = (1 + i ) − ( t 2 −t1 ) = u * ( t 1 , t 2 ); con 0 < u * ( t 1 , t 2 ) < 1
C 2 L( t 1; t n ) (1 + i ) t n −t1
[6.]
de forma que:
verificándose:
C1 = C 2 ⋅ u * (t 1 , t 2 ) = C 2 ⋅ (1 + i)t1 - t 2 = C 2 ⋅ (1 + i)-(t 2 - t 1 )
u( t 1 , t 2 ) =
1
u * ( t1, t 2 )
[7.]
[8.]
Si se considera una cuantía unitaria, el factor de actualización puede interpretarse como el capital equivalente, en
t1 , a una unidad de capital situada en t2.
Representación gráfica.
Problema 1: Obténgase el valor equivalente dentro de dos años, a 1000 euros disponibles hoy, si se valora en
capitalización compuesta al 5% efectivo anual.
Problema 2: Obténgase el valor actual de 1000 euros disponibles dentro de dos años y medio, si se valora en
capitalización compuesta al 3% semestral.
Los factores financieros verifican la propiedad multiplicativa para intervalos consecutivos. Supuesto t1< t2< t3, se
verifica:
u ( t 1, t 2 ) ⋅ u ( t 2 , t 3 ) = u ( t 1, t 3 )
[9.]
ya que:
L( t 1 ; t n ) L( t 2 ; t n ) L ( t 1 ; t n )
.
=
= u( t 1 , t 3 )
L ( t 2 ; t n ) L( t 3 ; t n ) L ( t 3 ; t n )
[10.]
Obviamente, también se cumple:
u * ( t 1, t 2 ) ⋅ u * ( t 2 , t 3 ) = u * ( t 1, t 3 )
[11.]
2
Caso de que los tipos de interés aplicables a los distintos períodos no sean iguales. Si se representa por
{i 1 , i 2 ,..., i n } los tipos de interés vigentes en cada uno de los subperiodos {( t 0 , t 1 )( t 1 , t 2 )....( t n −1 , t n )} en los que
se ha dividido un horizonte temporal (t0 ,tn ), entonces:
n
n
h =1
h =1
u(t 0 , t n ) = ∏ (1 + i h ) , con lo que: C n = C 0 ⋅ u(t 0 , t n ) = C 0 ⋅ ∏ (1 + i h )
n
[12.]
n
u * (t 0 , t n ) = ∏ (1 + i h ) −1 , con lo que: C 0 = C n ⋅ u * (t 0 , t n ) = C n ⋅ ∏ (1 + i h )− 1
h =1
[13.]
h =1
Problema 3: Obténgase el valor equivalente, dentro de tres años, a 1000 euros disponibles hoy, si se valora en
capitalización compuesta con los siguientes tipos de interés anuales : i1=4,50%; i2=5,00%; i3=5,25%.
Problema 4: Obténgase el valor actual de 2000 euros disponibles dentro de dos años, si los tipos de interés anuales
son: i1=4,50%; i2= 5,00%.
3. RÉDITO
El rédito es el incremento de cuantía generado en el intervalo [t1,t2] por cada unidad de capital situada en t1:
r( t 1 , t 2 ) = u( t 1 , t 2 ) − 1 =
L( t 1 ; t n ) − L ( t 2 ; t n )
= (1 + i )( t 2 −t1 ) − 1
L( t 2 ; t n )
[14.]
Obsérvese que, a partir de la ecuación [14.], se puede obtener el interés asociado al intervalo (t1, t2):
[
]
I = C ⋅ r( t1, t 2 ) = C ⋅ (1+ i )( t 2 − t 1 ) − 1
[15.]
La información proporcionada por el rédito resulta insuficiente, ya que se refiere al incremento sufrido por cada
unidad de cuantía en el intervalo y resulta difícil la comparación de los resultados cuando los réditos se refieren a
intervalos de diferente amplitud. Para resolver este problema se introduce el concepto de tanto o tipo de interés.
4. TANTO O TIPO DE INTERÉS.
Se denomina tanto, o tipo de interés, del intervalo (t1,t2) al incremento de cuantía producido en dicho intervalo
por cada unidad de cuantía situada en t1 y por unidad de tiempo. Es decir, el tipo de interés será el rédito
dividido por la amplitud del intervalo. Así,
i ( t 1, t 2 ) =
u ( t 1, t 2 ) − 1
( t 2 − t1 )
=
L( t 1; t n ) − L( t 2 ; t n ) (1 + i ) t 2 −t1 − 1
=
L( t 2 ; t n ).( t 2 − t 1 )
( t 2 − t1 )
[16.]
Para el caso de intervalos unitarios (t, t+1), es decir, n =1, el tipo de interés tomará la expresión:
i( t , t + 1) =
(1 + i ) − 1
=i
1
[17.]
Por tanto, puede decirse que el parámetro i de la ley de capitalización compuesta representa el tipo de interés
para intervalos unitarios (en la práctica, generalmente el año).
3
4.1. Tipo de interés efectivo y tipo de interés nominal
El tipo de interés de la ecuación [17.] -que habitualmente se denomina tipo de interés efectivo- depende de la
unidad de tiempo con la que se esté trabajando. Mientras no se indique expresamente lo contrario, por i(t,t+1) se
entenderá el tipo de interés efectivo anual.
Es bastante usual que los períodos en los que se genera el interés sean de amplitud distinta al año. Aparecen así dos
nuevos conceptos, el de tipo de interés efectivo subperiodal y el tipo de interés nominal.
Diremos que i(m) es el tipo de interés efectivo subperiodal equivalente al tipo de interés efectivo anual i si se
verifica que:
(
)
(1 + i ) = 1 + i ( m ) m
[18.]
Así pues, el tipo de interés efectivo subperiodal equivalente al tipo de interés efectivo i, es aquel tipo de interés
constante al que deberíamos reinvertir una unidad monetaria durante m subperiodos consecutivos de
amplitud (1/m) para que en t+1 se genere una cuantía i por unidad de capital invertido en t.
Problema 5
Calcúlese el capital que se obtendría al final del año si se invirtieran 1000 euros al 5% anual o al 0,12272%
trimestral.
Por otro lado, si i(t,t+1) es el tipo de interés correspondiente al período unitario (t, t+1) y subdividimos dicho
periodo unitario en m subperiodos de amplitud (1/m), el tipo de interés nominal correspondiente a un intervalo
cualquiera de amplitud (1/m), y que denotaremos por j(m), será:
j( m ) = i( t , t +
1
m
i)
(
)
(1 +
−1
1
)=
= m (1 + i )1/ m − 1 = m ⋅ i ( m )
m
1/ m
[19.]
Es decir, el tipo de interés nominal no es más que la proyección aritmética anual del tipo de interés
correspondiente a (1/m) de año y sin considerar, por tanto, el efecto de la posible reinversión de los
intereses.
Nótese que el tipo nominal debe venir acompañado de una mención a la frecuencia de generación m de los
intereses. Así, se hablará de tanto o tipo nominal anual de frecuencia m o pagadero m veces al año.
De las expresiones anteriores se puede obtener la relación entre i, i(m) y j(m):
(1 + i ) = (1 + i ( m ) ) = (1 +
de forma que:
j( m ) m
)
m
j( m )
m
j
(
m
)
)m − 1
i = (1 + i ( m ) ) m − 1 = (1 +
m
i ( m ) = (1 + i )1/ m − 1 =
[20.]
[21.]
[22.]
A partir de estas relaciones, resulta obvio que con un mismo tanto nominal, el tanto efectivo será mayor cuanto
mayor sea el fraccionamiento
Problema 6:
Supongamos un título con un valor de 1000 euros que paga intereses al 12% nominal anual, obténgase el tipo de
interés efectivo anual, en los siguientes supuestos:
m=1, los intereses se pagan de una vez al final de año:
m=2, los intereses se pagan con periodicidad semestral
m=12 , pago de intereses mensuales.
4
5. Rentas. Valor financiero de una renta.
Se denomina renta a todo conjunto de capitales asociados cada uno de ellos a un intervalo de tiempo. Cada uno de
los capitales que constituyen la renta recibe la denominación de término y cada uno de los intervalos a los que se
asocian recibe la denominación de período.
Las rentas pueden clasificarse de acuerdo con diferentes criterios:
1) Según el momento en que vencen los términos en cada período:
• Rentas pospagables.
• Rentas prepagables.
En las rentas prepagables los términos vencen al principio de cada período, mientras que en las rentas pospagables
los términos vencen al final de cada período.
2) Según que la duración de la renta sea finita o infinita:
• Rentas temporales.
• Rentas perpetuas.
3) Según la cuantía de los términos que la componen
• Rentas constantes.
• Rentas variables.
Dentro de las rentas constantes, se encuentran las rentas unitarias, que son aquéllas en las que todos los términos
tienen una cuantía igual a la unidad.
Las rentas variables reciben diversas denominaciones dependiendo de la ley de variabilidad de los términos:
variables en progresión geométrica, aritmética, etc.
4) Según la amplitud de los periodos:
• Rentas discretas: con periodos de amplitud finita (mensual, trimestral, anual, etc.)
• Rentas continuas: periodos infinitesimales.
En la realidad económica existen múltiples ejemplos de renta: salarios, pagos de préstamos, alquileres, etc. Para
obtener el valor financiero de una renta bastará con sumar financieramente los términos que la componen.
Problema 7
Obténgase el valor final e inicial de la siguiente renta anual, pospagable de términos (12.000; 1), (20.000; 2), (16.500;
3), (1.200; 4), si se valora en capitalización compuesta con un tipo de interés efectivo anual del 2,75%, para los dos
primeros años y del 3% para el resto.
No obstante, dado que en muchas ocasiones los términos de la renta son constantes, o sujetos a una ley de
variabilidad conocida (por ejemplo progresión geométrica), y que el tipo de interés de la ley de capitalización
compuesta con que se valoran es también constante, se pueden obtener unas expresiones específicas de la suma
financiera que facilitan el cálculo. Obtendremos a continuación las utilizadas con mayor frecuencia.
6. Valoración de rentas en capitalización compuesta y a tipo de interés constante.
6.1 Renta constante, pospagable y temporal
La renta unitaria, pospagable y temporal (con n términos) definida por el conjunto de capitales
5
{(1, t1 )(1, t 2 ).....(1, t n )} y valorada con una ley de capitalización compuesta con un tipo de interés efectivo periodal
i tendrá la siguiente representación gráfica:
t0
1
1
....
1
1
t1
t2
.....
tn-1
tn
Su valor financiero en t0, valor inicial o actual, representado por ∂ n
∂n
i
con n ∈ N será:
n
i
= (1+ i )−1 + (1 + i )− 2 + ... + (1 + i ) − n = ∑ (1+ i )− s
s =1
[23.]
y dado que se trata de la suma de los términos de una progresión geométrica de primer término a 1 = (1 + i ) −1 ,
último a n = (1+ i )−n , y razón q = (1+ i ) −1 , se puede escribir como:
∂n i =
(1 + i )−1 − (1 + i )− n (1 + i )−1
1 − (1 + i )−1
=
1 − (1 + i )−n
i
De igual forma, su valor financiero en tn, valor final, representado por S
n i
[24.]
es:
n −1
S n i = 1+ (1+ i ) + (1+ i )2 + ... + (1+ i )n −1 = ∑ (1+ i )s
s =0
[25.]
y como nuevamente se trata de una suma de términos variables en progresión geométrica, esta vez creciente, se
puede escribir como:
Sn i =
Obsérvese que se verifica:
S n i = (1 + i )n .∂ n i
(1+ i )n − 1
i
[26.]
donde (1+i)n es el factor de capitalización del intervalo [t0 ,tn].
Cuando en lugar de una renta de cuantía unitaria se trate de una renta con términos de cuantía constante C, tal y
como la representada en el esquema:
t0
C
C
t1
t2
....
.....
C
C
tn-1
tn
Sus valores inicial y final serán respectivamente:
V0 = C ⋅ ∂ n i
[27.]
Vn = C ⋅ S n i
[28.]
verificándose igualmente la relación:
Vn = V0 ⋅ (1+ i )n
o la recíproca:
V0 = Vn ⋅ (1+ i ) −n
[29.]
6
Hay que recordar que el valor financiero de una renta es un capital financiero. Por tanto, una vez conocido éste en
un punto cualquiera para obtener su valor en un momento distinto bastará con multiplicar dicho valor por el
correspondiente factor de capitalización o de actualización.
Problema 8
Dada una renta pospagable de 5 años de duración y término anual constante de 12.000 euros, con origen el
15/02/03 y final el 15/02/08, obténgase su valor en los siguientes puntos:
a) t0=15/02/03
b) tn=15/02/08
c) tτ= 15/02/06
d) tτ’=15/05/10
e) tτ’’=15/01/00
si se valora en capitalización compuesta a un tipo de interés efectivo anual del 3,75%.
Problema 9 Dada una renta pospagable de términos mensuales de 1.000 euros, obténgase:
a) Su valor inicial y final si el tipo de interés de valoración es sucesivamente: 3%, 4%, 8% anual y la renta tiene 3
años de duración.
b) Su valor inicial y final si el tipo de interés de valoración es el 3% anual y la renta tiene sucesivamente, 1, 5, y 10
años de duración.
6.2. Renta constante, pospagable y perpetua.
El valor inicial de una renta unitaria pospagable y perpetua se obtendrá como el límite del valor actual de la
correspondiente renta unitaria temporal cuando n → ∞ . Así:
∂ ∞ i = limn→∞
1 − (1 + i ) − n 1
=
i
i
[30.]
Y en el caso de la renta perpetua con términos de cuantía constante C será:
V0 = C ⋅ ∂ ∞ i =
C
i
[31.]
Resulta obvio que el cálculo de los valores finales en las rentas perpetuas carece de sentido.
Ejemplo 10: Obténgase el valor actual de una renta perpetua de términos anuales de 3.000 euros y valorada al
2,75% anual.
6.3 Renta de términos variables en progresión geométrica, pospagable y temporal.
Sea la renta de términos ( C; t 1 )( C ⋅ q; t 2 )( C ⋅ q 2 ; t 3 )L( C ⋅ q n −1; t n )
esquema.
t0
C
C.q
C.q2 ....................................
t1
t2
t3
....................................
con q > 0 y representada por el siguiente
C.qn-2
C.qn-1
tn-1
tn
7
Teniendo en cuenta que nuevamente se trata de la suma de términos de una progresión geométrica, su valor actual,
asumiendo un tipo de interés constante i, será:
V0 = A ( C; q )n i = C(1 + i ) −1 + C ⋅ q(1+ i ) −2 + L + C ⋅ q n −1(1 + i ) −n =
[32.]
1 − q n (1 + i ) − n
=C
1+ i − q
En el caso particular de que q = (1+ i ) esta expresión nos conduce a una indeterminación, por lo que deberá
obtenerse directamente el valor actual de la renta:
A ( C; (1+ i ))n i = C(1 + i )−1 + C(1+ i )(1+ i ) −2 + L + C(1 + i )n −1(1+ i )n = C (1 + i ) −1 ⋅ n
[33.]
El valor final de una renta de este tipo en el caso general sería:
Vn = S( C; q )n i = C ⋅ q n −1 + C ⋅ q n − 2 (1 + i ) + L + C(1+ i )n −1 = C
(1+ i )n − q n
1+ i − q
[34.]
verificándose obviamente la relación:
S( C;q )n i = A ( C;q )n i ⋅ (1 + i )n
[35.]
En el caso particular de q = (1+ i ) , el valor final tendrá la siguiente expresión:
S( C; q )n i = C(1 + i )n −1 ⋅ n
[36.]
Problema 5
Obténgase el valor actual y final de una renta anual, pospagable, de 15 años de duración, y términos crecientes en
progresión geométrica un 2% anual, si se valora en capitalización compuesta con un tipo de interés del 5% efectivo
anual y el primer término tiene una cuantía de 1000 euros.
6.4 Renta de términos variables en progresión geométrica, pospagable y perpetua.
En el caso de la renta perpetua, su valor inicial se obtiene a través del límite de la renta temporal cuando el número
de términos “n” tiende a infinito. Así:
V0 = A
( C ; q )∞ i
= lim A ( C; q )n i
n →∞
n

 q 
1− 

 C

, si q < 1 + i
1
+
i



 lim C
= 1 + i - q

= n → ∞
1+ i - q
 ∞ , si q > 1 + i


 lim n C (1 + i) -1 = ∞ , si q = 1 + i
n →∞
[37.]
Por tanto, sólo tiene sentido la renta perpetua variable en progresión geométrica cuando q < 1 + i .
8
Problema 6
Obténgase los valores actuales de una renta pospagable, perpetua, variable en progresión geométrica de razón q
=1,025, cuyo primer término tiene una cuantía de 500 euros si se valora en capitalización compuesta al 3,75% y al
2,5% efectivo anual.
6.5 Renta pospagable con fraccionamiento aritmético uniforme.
El fraccionamiento aritmético de una renta consiste en dividir cada una de las cuantías de sus términos en “m”
subcuantías, tales que su suma aritmética sea la cuantía inicial, y descomponer cada período en “m” subperíodos,
asociando cada subcuantía a uno de los subperíodos.
El fraccionamiento aritmético de frecuencia “m” en una renta definida por “n” términos la transforma en otra renta
de “n x m” términos, siendo la suma aritmética de las cuantías igual en ambas rentas, pero no así su valor
financiero.
Cuando el fraccionamiento, tanto de cuantías como de períodos, se hace en partes iguales se denomina uniforme.
En este caso, las “m” subcuantías serán iguales entre sí e iguales a
CS
. Dada una renta cualquiera con el siguiente
m
esquema:
t0
C1
C2 ....................
Cs-1
t1
t2 .....................
ts-1
Cs ...................
Cn-1
ts .................... tn-1
Cn
tn
La renta fraccionada de frecuencia “m” con fraccionamiento uniforme es la que surge al descomponer cada cuantía
y cada período en “m” partes iguales, de tal forma que para un subperíodo cualquiera (s-1, s] se verifica lo siguiente:
CS
ts-1
ts
Cs/m
ts-1
t s −1 +
1
m
Cs/m ........................
t s −1 +
resultando m subperíodos de amplitud
2
.......
m
t s −1 +
Cs/m
(m − 1)
m
Cs/m
ts
1
.
m
Un ejemplo de renta fraccionada uniforme es el sueldo de un empleado que percibe mensualmente una retribución
anual de C euros, correspondiéndole cada mes una cuantía mensual de C/12 siendo cada mes 1/12 de año.
El valor financiero en ts de todos los términos del período de esta renta fraccionada en base a una ley de
capitalización compuesta con un tipo de interés efectivo i será:
2
( m −1) 
1

CS 
C (1+ i ) − 1
i
i
m
m
1 + (1 + i ) + (1 + i ) + L + (1 + i ) m  = S
=
=
[38.]
C′S =
C
C
S
S
1
 m
m 
j( m )
m ⋅ i( m )


(1 + i ) m − 1
9
La renta fraccionada es, por tanto, financieramente equivalente a otra renta sin fraccionar de términos:


i
 C S
, t S 
 j( m ) 
[39.]
El fraccionamiento uniforme en rentas pospagables de periodo unitario equivale a multiplicar las cuantías de sus
i
. Así, sus valores inicial y final adoptarán la siguiente forma:
j( m )
términos iniciales (sin fraccionar) por el factor
n
V0 = ∑ C S
S =1
n
Vn = ∑ C S
S =1
En consecuencia, el coeficiente
i
i
(1 + i )− s = C S
∂
j( m ) n i
j( m )
[40.]
i
i
S
(1 + i )n − s = C S
j( m ) n i
j( m )
[41.]
i
juega el papel de operador de transformación de la renta sin fraccionar en la
j( m )
correspondiente renta fraccionada. Las rentas fraccionadas se denotan habitualmente por un exponente “(m)”.
Así, se pueden plantear las siguientes relaciones para el caso de rentas unitarias:
i
⋅∂
j ( m) n i
i
=
⋅s
j ( m) n i
∂ (nmi ) =
[42.]
s (nmi )
[43.]
Obsérvese que i>j(m) siempre que y cuando m>1. Es asimismo importante tener en cuenta que en las rentas
fraccionadas todas las variables deben ir expresadas en términos anuales: tipo de interés efectivo anual, tanto
nominal anual, número de períodos anuales y cuantía anual
Para el caso de rentas de cuantía constante C se mantiene la misma relación:
i
⋅∂
j ( m) n i
i
=C⋅
⋅S
j ( m) n i
V0 = C ∂ (nmi ) = C ⋅
Vn = C S n( mi )
[44.]
[45.]
Y lo mismo ocurre para cualquier otro tipo de rentas (perpetuas, variables en progresión geométrica,...). En general,
tendríamos lo siguiente:
i
⋅ (Va ) n i
j ( m)
i
=
⋅ (V f ) n i
j ( m)
Valor inicial: (Va ) (nmi ) =
Valor final: (V f ) (nmi )
[46.]
[47.]
Problema 7
Obténgase el valor actual de las siguientes rentas sabiendo que se valoran en capitalización compuesta con un tipo de interés
efectivo anual del 4%.
a) Una renta de términos mensuales, pospagables, constantes durante el año y crecientes cada año un 1,5% acumulativo y 10
años de duración. La cuantía del primer término es de 500 euros.
b) Una renta de términos mensuales constantes de 900 euros de cuantía y 5 años de duración.
10