Análisis de conglomerados

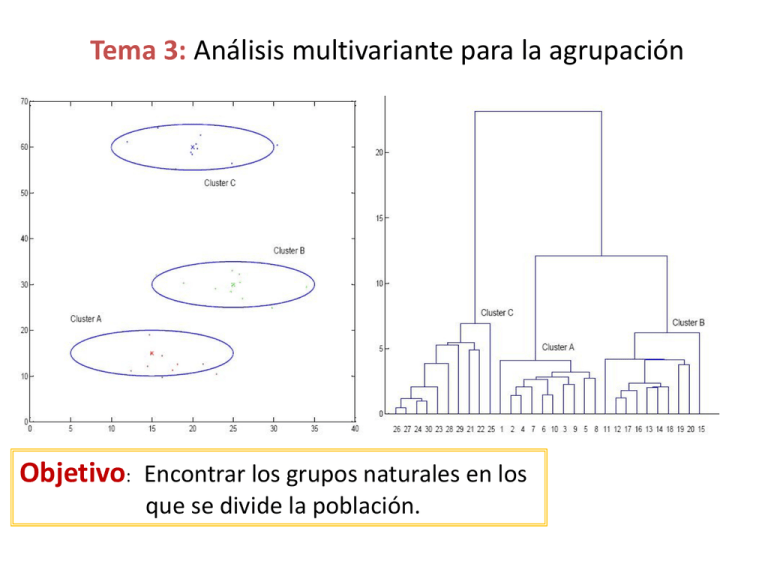
Tema 3: Análisis multivariante para la agrupación
Objetivo: Encontrar los grupos naturales en los
que se divide la población.
Ejemplo canónico en Biologia:
Taxonomía
Rosa doméstica
Reino:
Plantae (Plantas)
Grupo:
Tracteophyta (planta vascular)
Subgrupo: Pteropsida (planta de helechos y semillas)
Clase:
Dicotyledoneae
Orden:
Rosales
Familia: Rosaceae (Cerezas, ciruelo, espino, rosas y relativos
Género: Rosa
Especia: Galliea (Rosa domestica)
 La clasificicación procede de lo mas nátural a lo mas particular
 Demografía, Medio ambiente (vulnerabilidad de los acuíferos)
La técnica de subdividir una población en distintos
grupos se llama
Cluster Analysis
(Análisis de conglomerados)
¡Malas noticias! El análisis de conglomerados es
altamente empírico. Hay distintos métodos que pueden dar
lugar a muy diferentes grupos.
Además, como los grupos
Son desconocidos a priori es difícil juzgar los resultados
Problema de clasificación
Dada una matriz de datos X correspondiente a n individuos,
el problema consiste en asignar los n individuos a k grupos
siguiendo dos reglas
Regla I: Cada elemento se asigna a un único grupo
Regla II: Cada grupo es homogeneo internamente
¿Cómo medimos la homogeneidad de un grupo?
(similitudes)
Regla III: Distintos grupos son heterogeneos
(distancias)
Similitudes y distancias
Nota:
Para este problema se utiliza la noción de distancia Euclidea. La distancia
de Mahalanobis nos añadiría mas información pero como no sabemos los grupos no
conocemos las correspondientes matrices de varianzas covarianzas.
Matriz de
distancias
Nota II:
Dependiendo del problema nos interesa trabajar con las variables estandarizadas
o no (A veces interesa dar mas peso a las variables con magnitudes mas grandes) . En un
Problema real puede ser conveniente hacer ambas
Nota III:
No siempre lo mas conveniente es usar la distancia Euclidea
(Distancia de Manhattan, Minkowski..)
Nota IV:
Si las variables toman valores en los que las unidades son ficticias
(Variables cualitativas) nos interesa cambiar el concepto de distancia por
El de
Similitudes
Variables binarias (o dicotómicas)
X1
X2
X3
0
hombre
1
mujer
0
fumador
1
No fumador
0
sobrepeso
1
Sin sobrepeso
Similitudes
Supongamos dos observaciones de p-variables binarias
xi
[1,0,0,1,0,1] x j
[1, 0,1, 0, 0,1]
Definiciones
a=Número de veces que ambas observaciones tienen 1
b= Número de veces que la observación i tiene 1 y la j 0
c=Número de veces que la observación j tiene 0 y la i 1
d=Numero de veces que ambas tienen 0
Proporción de
coincidencias
Proporción de
apariciones
Matriz de similitudes
Métodos de agrupación
Métodos jerárquicos: Los grupos van creciendo de mas a menos homogéneos
Métodos no jerárquicos: Se forman grupos homogéneos, pero no se establecen
relaciones dentro de los grupos
Jerarquicos
Los que estudiaremos
De Aglomeración; Parten de elementos individuales y (usando similitudes o
distancias ) las van agregando a grupos
De división
; Parten del total como un único grupo y lo van dividiendo
sucesivamente hasta llegar a los elementos individuales
Descripción del metodo jerárquico de
aglomeración
Punto de Partida: La matriz de similitudes o matriz de distancias.
La matriz de similitudes
N=5
1- Comenzamos con n clusters con un solo elemento
2- Buscamos en la matriz de similitudes (distancias)
el par con mayor similitud (menor distancia) e.g U V
A (Agrostis tenuis) y F(Festuca Rubra)
3- Unimos los cluster es U y V formando uno nuevo UV. Y actualizamos la
Matriz ahora con N-1 clusteres.
4- Repetimos los pasos 2 y 3 hasta quedarnos con un único cluster
¿????
Se comparan
Los mas cerca
nos
Se comparan
Los
Mas lejanos
Se comparan
Los centroides
¡Distintos métodos dan lugar a distintos clusteres!
Park Grass con Encadenamiento simple o vecino mas próximo
=
¡AF y D son los mas cercanos!
Calculamos la nueva matriz de similitudes
Solo nos quedan 3 clusteres,
AFD, B y C
¡AFD y B son los mas cercanos!
Calculamos la nueva matriz de similitudes
Representanciones del algoritmo
jerárquico
I: Historial de Conglomeración
Parte Importante
II: Dendograma
Ejemplos tipos de maiz en venezuela
Variables demográficas
Otros métodos
Vecino mas lejano
Paso I: empezamos con la misma matriz que nos da el mismo cluster AF
Paso II: Ahora el cálculo de la distancia entre clusters es diferente!
Paso III: y asi seguimos --
Resultado
Método de centroides (distancias)
¡ La respuesta es diferente!
Problema:¿ Como decidir cuantos
grupos significativos hay?
Respuesta: Anova, A. Discriminante SENTIDO COMÚN (INFORMACIÓN
EXTERNA), SCDG
Respuesta: Se corta el dendograma en un lugar sensato de manera que los
Clusteres seleccionados tengan alguna significación.
Ejemplos tipos de maiz en venezuela
Métodos no jerarquicos (K-medias)
Paso I: Decidimos cuantos grupos queremos (K)
(despues veremos un criterio)
Paso II: Asignamos aleatoriamente n/K elementos a
cada grupo. Tenemos K grupos
K
1
i
Paso III: Hallamos el centro de cada grupo. Obtenemos
K centros x
i
Paso IV: Para cada elemento x_i hallamos su distancia
(Euclidea) a cada xk y le reasignamos al grupo
que la minimiza. Obtenemos K nuevos grupos
posiblemente distintos
2
Ki
Paso V=Paso III: Repetimos el proceso obteniendo nuevo
grupo
K
3
i
Paso V=Paso III: Repetimos el proceso hasta llegar a
una etapa j tal que
Ki
j
Ki
j 1
Criterio de homogeneidad : Suma del cuadrado de la
distancia entre los
Grupos (SCDG)
 Mide la homogeneidad entre los grupos (los grupos finales minimizan SCDG).
Metodo jerarquico de Ward.
 Criterio para decidir cuantos grupos
 Es un viejo conocido disfrazado
¿Cuántos grupos?
F>10
F<10
K+1 grupos seran mas homogeneos
No interesa hacer grupos mas pequeños
Tortugas I
Tortugas II
Cocodrilos
¿Qué clusters tienen interpretación?