Habilidades Matemáticas - UniversidadFinanciera.mx
Anuncio

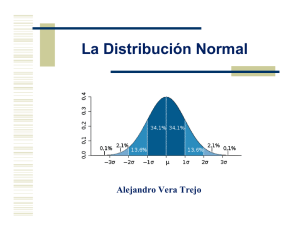
Habilidades Matemáticas Alejandro Vera La distribución normal Introducción Una de las herramientas de mayor uso en las empresas es la utilización de la curva normal para describir situaciones donde podemos recopilar datos. Esto nos permite tomar decisiones que vayan a la par con las metas y objetivos de la organización. En este módulo se describe la Distribución normal. Se utilizan ejemplos y ejercicios donde se enseña sobre la determinación de probabilidades y sus aplicaciones. Objetivo Identificar las propiedades de una distribución normal. Encontrar el área bajo una distribución normal estándar. Interpretar áreas bajo la curva normal de acuerdo a diferentes problemas y su aplicación al medio financiero. La distribución normal La distribución normal fue reconocida por primera vez por el francés Abraham de Moivre (1667-1754). Posteriormente, Carl Friedrich Gauss (1777-1855) realizó estudios más a fondo donde formula la ecuación de la curva conocida comúnmente, como la “Campana de Gauss". ¿Cuál es su Utilidad? Se utiliza muy a menudo porque hay muchas variables asociadas a fenómenos naturales que siguen el modelo de la normal. Caracteres morfológicos de individuos (personas, animales, plantas,...) de una especie, por ejemplo: tallas, pesos, diámetros, distancias, perímetros,... Caracteres fisiológicos, por ejemplo: efecto de una misma dosis de un fármaco, o de una misma cantidad de abono ¿Cuál es su Utilidad? Caracteres sociológicos, por ejemplo: consumo de cierto producto por un mismo grupo de individuos, puntuaciones de examen. Caracteres psicológicos, por ejemplo: cociente intelectual, grado de adaptación a un medio,... Comportamiento de los precios en el medio financiero, por ejemplo: los precios de las acciones, el tipo de cambio, la cotización de los metales. ¿Cuál es la función F(x)? ¿Cuál es la función F(x)? En la siguiente gráfica vemos la representación gráfica de la función de Z. ¿Cuáles son sus Propiedades? Es simétrica respecto a su Media. La moda y la mediana son ambas iguales a la media. Los puntos de inflexión de la curva se dan para x = μ − σ y x = μ + σ. En el intervalo [μ - σ, μ + σ] se encuentra comprendida, aproximadamente, el 68,26% de la distribución. En el intervalo [μ - 2σ, μ + 2σ] se encuentra, aproximadamente, el 95,44% de la distribución. Por su parte, en el intervalo [μ -3σ, μ + 3σ] se encuentra comprendida, aproximadamente, el 99,74% de la distribución. ¿Cuáles son sus Propiedades? ¿Qué es la estándar (σ )? desviación Compruebe el cambio de la distribución variando la desviación estándar ¿Qué es la media μ? Compruebe el cambio de la distribución variando la media Ejemplo En el siguiente histograma podemos observar la distribución de frecuencias por peso de acuerdo a la edad. De acuerdo a este teorema según aumenten la cantidad de dato se podrá trazar una curva que tome cada vez más formación en forma campana. ¿Cómo determinar el área bajo la curva normal? Paso 1 - Interpretar gráficamente el área de interés. Paso 2 - Determinar el valor Z Paso 3 - Encontrar el valor de Z en excel por medio de la función DISTR.NORM.ESTAND Paso 4 - Hacer la suma o resta de áreas para encontrar la probabilidad deseada Ejemplos y ejercicios Supóngase que se sabe que el peso de los/as estudiantes universitarios/as sigue una distribución aproximadamente normal, con una media de 140 libras y una desviación estándar de 20 libras. Determinar la probabilidad de que una persona tenga un peso menor o igual a 150 libras Ejemplo 1 Paso 1 Interpretar gráficamente el área de interés. Se establece que a=150 libras, por lo tanto el área de la curva de la curva requerida es: Ejemplo 1 Paso 2 - Determinar el valor Z: Z X 150 140 20 0.50 Paso 3 - Encontrar en excel el valor Z=0.50 con la función DISTR.NORM.ESTAND de aquí resulta que el área de 0.6915 Paso 4 - Hacer la suma o resta de áreas (de ser necesario) para encontrar la probabilidad deseada. Y la probabilidad de que una persona pese 150 lbs. o menos es de 0.6915 Ejemplo 2 Se desea obtener la probabilidad de que una persona elegida al azar, tenga un peso mayor o igual a 150 libras. Paso 1 Interpretar gráficamente el área de interés. Se establece que a=150 libras, por lo tanto el área de la curva buscada es: Ejemplo 2 Paso 2 - Determinar el valor Z: Z X 150 140 20 0.50 Paso 3 - Encontrar en Excel el valor Z=0.50 con la función DISTR.NORM.ESTAND el área es de 0.6915 Paso 4 - Hacer la suma o resta de áreas para encontrar la probabilidad deseada. El área de 0.6915 no representa el área requerida sino la contraria. En este caso se debe restar 1 a la probabilidad encontrada. 1 - .6915 = 0.3085 Ejemplo 3 Determinar la probabilidad de que una persona, elegida al azar, tenga un peso menor o igual a 115 libras Paso 1 Interpretar gráficamente el área de interés. Se establece que a=115 libras, por lo tato el área buscada es: Ejemplo 3 Paso 2 - Determinar el valor Z: Z X 115 140 20 1.25 Paso 3 - Encontrar en Excel el valor Z=-1.25 con la función DISTR.NORM.ESTAND el área es de 0.1056. En este caso la probabilidad de que una persona pese 115 lbs. o menos es de 0.1056 Ejemplo 4 Determinar la probabilidad de que una persona, elegida al azar, tenga un peso entre 115 y 150 libras. Paso 1 Interpretar gráficamente el área de interés. Se establece que a=115 libras y b=150 libras, por lo tanto el área de la curva buscada es: Ejemplo 4 Paso 2 - Determinar los valores de Z Cuando X=115 Z Cuando X=150 Z X 115 140 20 1.25 X 150 140 20 0.50 Paso 3 - Se encuentran los valores de Z=-1.25 y Z = 0.50, de donde las probabilidades resultan de: 0.1056 y 0.6915 respectivamente. Paso 4 - Al área de 0.1056 se le resta la de 0.6915 y el resultado es = 0.5858 Ejemplo 5 Determinar la probabilidad de que una persona elegida al azar, tenga un peso entre 150 y 160 libras. Paso 1 Interpretar gráficamente el área de interés. Se establece que a=150 libras y b= 160 libras, por tanto el área de la curva buscada es: Ejemplo 5 Paso 2 - Determinar el valor Z Z X 160 140 1.0 20 Paso 3 - Se encuentran los valores de Z Cuando Z = 0.50 el área es de 0.6915 Cuando Z = 1.0 el área es de 0.8413 Paso 4 - Al área de 0.8413 se el resta la de 0.6915 y el resultado es = 0.1499 Ejemplo 6 Determinar la probabilidad de elegir a una persona que pese entre 115 y 130 libras. Paso 1 Interpretar gráficamente el área de interés. Se establece que a=115 libras y b= 130 libras, el área de la curva que nos interesa es la siguiente: Ejemplo 6 Paso 2 - Determinar el valor Z para X=130 Z X 130 140 20 0.50 Paso 3 - Encontrar el valor de Z=-0.50 el área es de 0.3085 Paso 4 - Haciendo la resta correspondiente la probabilidad buscada resulta de 0.3085 - 0.1056=0.2029 Bibliografía Estadísticas para administración y economía, by David R. Anderson and Dennis J. Sweeney (Paperback - Jan. 2, 2008) Statistics for Business And Economics, by Paul Newbold, William Carlson, and Betty Thorne (Hardcover - Mar. 23, 2009) Elementary Statistics: A Step By Step Approach by Allan G. Bluman (Hardcover - Oct. 27, 2008) Habilidades Matemáticas Alejandro Vera