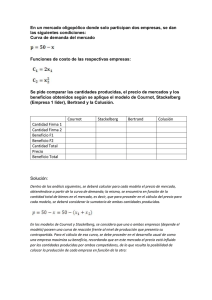
Teoría de Juegos y Modelos de Oligopolio

UNIVERSIDAD NACIONAL PEDRO RUIZ GALLO
LAMBAYEQUE - PERU
TEORIA DE JUEGOS
Y MODELOS DE OLIGOPOLIO1
Lindon Vela Meléndez2
(Alex F. Chapoñan Coronado, Grecia C. Alexis I., Díaz Acha, Inga Juarez, Ernesto Loayza Mori
y Cesar A. Sales Campos.)3
LAMBAYEQUE-PERÚ
2011
1
Apuntes de estudio del curso de Economía de la Producción (Organización Industrial), dictado en la Escuela de
Economía de la Universidad Nacional Pedro Ruiz Gallo de Lambayeque.
2
Economista, docente responsable de la materia.
3
Estudiantes del VII Ciclo de la Escuela de Economía de la UNPRG – Lambayeque, responsables de la
sistematización y aplicaciones.
Contenido
RESUMEN.............................................................................................................................. 3
PALABRAS CLAVE ............................................................................................................... 4
INTRODUCCION .................................................................................................................... 5
TEORIA DE JUEGOS Y MODELOS DE OLIGOPOLIO ......................................................... 6
SECCION I: INTRODUCCION A LA TEORIA DE LOS JUEGOS .......................................... 6
1.1. Interacción Estratégica .................................................................................................................. 6
2.1. Estrategias dominantes y dominadas ........................................................................................... 7
1.3. El equilibrio de Nash como concepto de solución ........................................................................ 8
SECCION II: TEORÍAS DE OLIGOPOLIO ESTÁTICO ........................................................ 10
1.1.
Modelo de Cournot ................................................................................................................ 10
1.1.1. Supuestos del modelo: ......................................................................................................... 10
1.1.2. Hipótesis de Cournot: ........................................................................................................... 10
1.1.3. Explicación del modelo de Cournot: .................................................................................... 11
1.1.4. Equilibrio Nash-Cournot ....................................................................................................... 13
1.1.5. Caso de “N” empresas .......................................................................................................... 13
1.2.
Modelo de Bertrand ............................................................................................................... 15
SECCION III: COMPETENCIA EN DOS ETAPAS ............................................................... 18
2.1. Modelo de Kreps-Scheikman: Rivalidad en dos Etapas...................................................... 18
2.2. Modelo de Stackelberg ............................................................................................................... 20
2.2.1. Equilibrio de Stackelberg ...................................................................................................... 21
2.2.2. Resultados ............................................................................................................................ 23
SECCION IV: EJERCICIO DE APLICACIÓN ....................................................................... 24
El grafico N° 10 correspondiente al ejercicio se muestra en los anexos. ....................... 27
V. CONCLUSIONES............................................................................................................. 28
REFERENCIAS .................................................................................................................... 29
ANEXOS .............................................................................................................................. 31
2
RESUMEN
El presente documento tiene como objetivo presentar de manera ordenada y breve
las principales conclusiones del estudio de los diferentes modelos de oligopolio,
mediante un análisis descriptivo de los mismos. En la primera sección se realiza una
breve reseña de conceptos substanciales de la teoría de los juegos, en la segunda
sección se describen los modelos estáticos de Cournot y Bertrand, en la tercera
sección se analizan los modelos de dos etapas de Kreps – Scheikman y Stackelberg
y finalmente se presenta un ejercicio de aplicación. En el presente estudio se
concluye que un modelo obtiene resultados diferentes que sirven de marco teórico
para estudiar la conducta de los diversos negocios reales.
ABSTRACT
This paper aims to present the main finding on the models of oligopoly in an orderly
and brief fashion, by using a descriptive analysis of the models. The first section is an
overview of the substantial concepts of game theory, the second section describes
the static models of Cournot and Bertrand.
The third section discusses the two-stage models of Kreps - Scheikman and
Stackelberg, and finally presents an application exercise. This study concludes that a
model obtains different results that serve as theoretical framework for studying the
behavior of the various real business.
3
PALABRAS CLAVE
Teoria de juegos, Modelos de oligopolio, Modelo de cournot, Modelo bertrand,
Modelo de stackelberg, Modelo de kreps-scheikman, Rivalidad en dos etapas,
Competencia estratégica
KEY WORDS
Game’s Theory, Oligopoly Models, Cournot Model , Bertrand Model, Stackelberg
Model, model-scheikman Kreps, Rivalry in two stages, Strategic Competition.
4
INTRODUCCION
En el mundo de los negocios observamos que la mayoría de corporaciones viven en
el terreno del oligopolio, esto es una industria que se caracteriza por la presencia de
pocas empresas, donde los productos que se ofrecen pueden o no ser diferenciados,
existen barreras de entrada: En este terreno, la interacción estratégica se produce a
diario, debido a ello cada decisión o estrategia que tome cada empresa afectara a
sus rivales. En ese sentido la teoría de juegos es de gran ayuda para analizar y
comprender las interacciones estratégicas.
En el caso del oligopolio no existe un solo modelo estándar como en competencia
perfecta y monopolio, debido a que diversos factores como las reglas de juego, la
información de la que disponen los jugadores y el sentido de oportunidad de las
acciones de cada uno dan como resultado diferentes escenarios posibles; esto no es
necesariamente una desventaja, ya que se cuenta con una gran variedad de
modelos; cada uno es apropiado para cierto de tipo de escenario en el mundo de los
negocios.
La importancia del estudio del oligopolio radica en que es el primer paso para
comprender el complejo mundo en que se desarrollan las grandes corporaciones.
Esperamos que este estudio contribuya con posteriores investigaciones.
5
TEORIA DE JUEGOS Y MODELOS DE OLIGOPOLIO
SECCION I: INTRODUCCION A LA TEORIA DE LOS JUEGOS
1.1. Interacción Estratégica
La teoría de juegos se divide en dos ramas importantes de estudio, teoría de juegos
no cooperativos y teoría de juegos cooperativos, la primera analiza principalmente al
jugador individual, es decir a la empresa;
la segunda supone una coalición de
jugadores o empresas
Existen dos supuestos básicos que subyacen a esta teoría, primero las empresas
son racionales, es decir persiguen firmemente la maximización de beneficios, el
segundo supuesto es que las empresas aplican esta racionalidad al proceso de
razonamiento estratégico, al momento de tomar decisiones los conductores de la
empresa emplean todo el conocimiento que tienen para formar expectativas de cómo
se comportaran las otras empresas.
Las decisiones o estrategias de las empresas se refieren a decisiones sobre
cantidades, variedades, calidades, y precios de los diferentes bienes y servicios
(Pisfil, 2008, citado en Antúnez, 2010).
Dichas estrategias producirán un resultado en el juego, que son en buena cuenta las
utilidades de las empresas que conforman el oligopolio. Pueden existir muchos
resultados, pero hay uno que es de equilibrio, es decir una combinación de
estrategias tal que ninguna empresa tiene un incentivo para cambiar la estrategia
que está aplicando, dado que tampoco lo hará ninguna de las otras empresas.
(Pepall, 2006)
Cuando las empresas interactúan estratégicamente, el resultado difiere cuando las
empresas tienen como variable estratégica el precio, cantidad u otra variable,
entonces la manera de predecir la forma en que actuaran ciertas empresas es poder
6
contar con información de la estructura de mercado y opciones disponibles para las
demás empresas. Por otro influye también si la interacción estratégica es secuencial
o simultanea, en el primer caso las empresas hacen sus elecciones una después de
otra, en el segundo caso ambos jugadores toman sus decisiones al mismo tiempo,
pero en ambos casos se supone que los jugadores conocen las opciones
estratégicas que disponen las demás empresas.
1.2. Estrategias dominantes y dominadas
En algunos casos ciertas estrategias de las empresas suelen ser dominadas es decir
están descartadas para lograr la maximización de utilidades, por ende no será
escogida ya que es la peor de todas las alternativas independientemente de lo que la
otra u otras empresas elijan.
Para una mayor comprensión de lo anterior se coloca un ejemplo a continuación
Dos aerolíneas, Delta y American, ofrecen un viaje de Boston a Budapest, cada
empresa ya estableció un precio pero aun no determina el horario de salida y ambas
empresas tomaran esta decisión al mismo tiempo. Un estudio de mercado concluye
que 70% de los posibles clientes prefiere salir de Boston por la tarde, mientras que
30% prefiere salir por la mañana., ambas empresas conocen esto y también saben
que si escogen la mismas opciones se dividirán el mercado, el grafico N°1 muestra la
matriz de pagos. (Véase en anexos)
Veamos lo que sucede con Delta, si elige ofrecer un vuelo por la mañana, obtendrá
dos posibles resultados un pago de 15% en caso de que American elija también la
opción de vuelo por la mañana y un pago de 30% en caso de que American elija la
opción de vuelo por la tarde. Por otro lado si Delta elige ofrecer vuelos por la tarde
tendrá dos posibles resultados 70% y 35%, según la elección de American, de esto
se puede fácilmente deducir que la mejor opción para Delta es elegir ofrecer vuelos
por la tarde ya que sin importar la elección de American siempre obtendrá mejores
7
resultados eligiendo ofrecer vuelos por la tarde. En ese caso la estrategia dominada
es la del vuelo matutino.
De la misma forma se realiza el análisis colocándose en los zapatos de la empresa
American, el resultado será el mismo, la opción mañana es descartada, por tanto
ambas escogerán siempre el horario de salida por la tarde y ninguno tendrá un
incentivo para cambiar su decisión.
En contrapartida podemos analizar la estrategia dominante, la cual es una estrategia
que ofrece los mejores resultados que cualquier estrategia de una empresa,
independientemente de lo que hagan sus rivales, es decir esta estrategia dominante
hace que las utilidades o resultados de las empresa sean las mejores, pero esto no
significa que obtendrá las mejores de toda la industria, ya que esto depende de la
estructura propia del juego. A veces se dan casos en que la empresa no tiene
estrategias dominantes ni dominadas, pero para una empresa que tiene una
estrategia dominante lo mejor es usarla, aquí no es necesario realizar un análisis
exhaustivo.
1.3. El equilibrio de Nash como concepto de solución.
Ahora vamos a suponer que la variable de decisión de la empresa ya no son los
horarios sino los precios, Supongamos que existen 60 consumidores dispuestos a
pagar hasta $500 y otros 120 consumidores dispuestos a pagar hasta $220. Si
amabas aerolíneas establecen el mismo precio se dividirán el mercado. El costo
unitario por pasajero es de 200$. Si Delta y American establecen un precio alto de
$500 se dividirán el mercado y cada aerolínea servirá a la mitad de los 60 pasajeros
dispuestos a pagar el precio de $500, por tanto los beneficios de cada una serán
30*(500) – 30*(200)= $9000, por otra parte si cada empresa elige un precio bajo,
todos abastecerán toda la demanda (180 pasajeros), los beneficios de cada una
serán 90*(220)-90*(200)= $1800.
8
Cuando una aerolínea elige un precio alto y la otra un precio bajo, la primera no
obtiene beneficios ya que no venderá un solo pasaje, entre tanto la empresa que
opto por el bajo precio obtendrá 180*(220-200)= $3600 de utilidades.
El Grafico N°2 muestra la matriz de pagos de utilidades de las aerolíneas en cada
caso explicado anteriormente. (Véase en anexos)
Lo primero que se observa es que no existen estrategias dominadas ni dominantes
para ninguna de las empresas, lo que sugiere esta matriz es que una empresa debe
elegir la misma opción que la otra. Pero ¿cómo llegamos a una elección optima?. La
respuesta radica en las expectativas que tenga una empresa por otra, si Delta espera
que American elija la opción de precio bajo, Delta también hará lo mismo, Delta sabe
también que American sabe que ella elijará la tarifa baja. Esto significa un equilibrio
de Nash, ya que ninguna tendrá incentivos para cambiar de estrategia, elegida la
opción de tarifa baja.
Pero si analizamos la estrategia de tarifas altas ($9000, $9000), nos damos cuenta
que también es un equilibrio de Nash. La concentración en el equilibrio de Nash
permite eliminar dos combinaciones pero no permite encontrar un resultado único,
por ello se debe considerar otros factores como la experiencia previa y el aprendizaje
de los gerentes, si ellos ya han estado por muchos años en el negocio entonces
conocen el mismo y pueden saber cómo actuaran los gerentes de las otras
empresas, lo contrario ocurre con gerentes inexpertos, por lo que se deduce que
ellos aseguraran las utilidades eligiendo tarifas bajas.
9
SECCION II: TEORÍAS DE OLIGOPOLIO ESTÁTICO.
1.1. Modelo de Cournot
El modelo de Cournot es un modelo estático de oligopolio en donde la elección o
variable estratégica de las empresas manejan para su competencia es el volumen de
la producción.
1.1.1. Supuestos del modelo:
 Las empresas venden productos homogéneos.
 La variable estratégica es la cantidad de producción.
 Cada empresa decide independiente y simultáneamente la cantidad que
producirá del bien.
 Tienen igual función de costos: CTi= cqi. No tienen costos fijos.
 No enfrentan restricciones de capacidad, pueden servir toda la demanda que
reciban.
“Este modelo quizás el más simple presenta un duopolio (2 empresas), asumiendo
que los costos eran iguales y que las dos firmas tienen productos homogéneos.”
(Antúnez Irgoin, 2010, p.4)
1.1.2 Hipótesis de Cournot:
El precio que se obtiene en el mercado es el producto de la suma de las ofertas
individuales de cada firma, esto sería la oferta agregada de las empresas.
Cournot afirmó que cuando las empresas fijan la cantidad de producción que
maximizan sus beneficios, cada empresa supone que la otra va a mantener
constante su nivel de producción elegido; es decir la variable estratégica manipulada
por cada empresa es la cantidad producida, dichas
cantidades son escogidas
simultáneamente. El beneficio de cada empresa es función de la cantidad producida
10
por esa empresa y del precio de mercado, que a su vez es función de la cantidad
producida por ambas empresas.
Donde la condición de maximización de beneficios es
Pero el ingreso marginal Img (qi;qj) a diferencia de un monopolio Img (qi). Una vez
que las empresas fijan la cantidad de producción está también queda fijada en el
mercado (Q = qi+ qj) y una vez fijada la cantidad también queda fijado el precio.
Si suponemos que existe un mercado donde actúa una sola empresa, la
llamaremos empresa 1, existe otra que quiere entrar en el mercado: empresa 2. La
empresa 2 puede ofrecer un producto homogéneo al ya existente en el mercado
ofrecido por la empresa 1 y al mismo costo. Evidentemente si la empresa 2 ingresa al
mercado y produce su bien la empresa 1 reaccionara usando una estrategia optima
es decir un nuevo nivel de producción que maximice sus utilidades dado el nivel de
producción del rival. Estableciendo así que cada empresa posee una reacción de
maximización de utilidades, es decir una respuesta única. Cournot representa
gráficamente estas respuestas como curvas de reacción, a las cuales algunos
autores prefieren llamar funciones de mejor respuesta.En el grafico N°3 se aprecia
lo anteriormente señalado.(Véase en anexos)
La función de mejor respuesta se obtiene del proceso de maximización de beneficios
de la empresa, teniendo en cuenta las decisiones de la otra empresa.
1.1.3. Explicación del modelo de Cournot:
En una investigación (Pérez-Reyes, 2006) la demanda del mercado D0 es abastecida
por una sola empresa, el monopolista maximiza sus utilidades en q M.Si consideramos
que entra un competidor, el efecto que esto generará es una reducción de la
demanda del mercado en el valor de lo producido por el entrante, de forma que la
nueva demanda que enfrenta la firma establecida es D 1. Con la misma deducción
que cada decisión de aumentar la producción del entrante reduce el nivel de
11
producción que maximiza las utilidades de la empresa establecida. Por lo tanto para
cada nivel de producción de los competidores, habrá un nivel de producción óptima
para la empresa 2: función de reacción de la empresa 1.
El grafico N° 4 representa la interacción de la empresa en el mercado para luego
obtener la función de reacción. (Véase en anexos)
Consideremos que ocurre con la función de reacción de la empresa 1 cuando se
incrementa su costo marginal. El incremento del costo marginal de la empresa 1
hace que su función de reacción se desplace hacia la izquierda. El nivel de
producción, de uno de los extremos sigue siendo el de la competencia perfecta, sólo
que bajo costos distintos.Elgrafico N°5 representa la curva de la función de reacción
que deriva de los movimientos de las empresas en el mercado.(Véase en anexos)
Si Q es la cantidad total de demanda cuando el precio es cero, entonces se puede
concluir que la empresa 1 producirá la mitad de Q, es decir q1, cuando el precio es p1.
Esto es así porque q1 es el punto donde se cortan el ingreso marginal es igual al
costo marginal nulo. El beneficio obtenido por 1, es igual a la demanda del área
PRq0. En el segundo momento, interviene una empresa 2 que considera que 1
seguirá produciendo la mitad del mercado. Esta demanda D 2, es igual a la demanda
total de mercado menos la cantidad producida por 2. Esta demanda D2, produce ¼
del total y obtiene un beneficio igual al área PTq0. La empresa 2 cobra un precio
menor a P2, a reacciona con la creencia de que 2 seguirá produciendo q2. Por lo
tanto, se tiene una demanda dirigida a 1 que es demanda total menos la parte
producida por 2 que es igual ¼ del mercado. Esto dará lugar a que q 3 es ahora 3/8
de la demanda total Q.
Esto da lugar a que 2 produzca 5/16 de la demanda total y si continúa así hasta el
infinito.
12
1.1.4. Equilibrio Nash-Cournot
Si se grafica la función de reacción de ambas empresas, para el caso de un duopolio.
Se podrá observar que se determinan cuatro áreas.El equilibrio de mercado se logra
cuando ambas funciones de reacción se crucen, punto E, ello definirá el nivel de
producción de equilibrio que le corresponde a cada empresa. Para el caso analizado,
de costos iguales, el nivel de producción será el mismo en el óptimo, para ambas
empresas, y por lo tanto tendrán la misma participación de mercado.Elgrafico N°6
representa lo explicado anteriormente.(Véase en anexos)
1.1.5. Caso de “N” empresas
En la búsqueda de ampliar nuestro conocimiento para el análisis del modelo de
cournot, ahora trabajaremos con el caso general de N empresas. Continuamos con el
supuesto de productos homogéneos con igual costo.
Ahora la demanda de la industria será:
P= A – BQ
Donde Q= q1 + q2 +………+ qN Q es la sumatoria de la producción de las N
empresas es decir:
Q=
Q-1 sería la suma de la producción de toda la industria menos la de la empresa 1.
Las utilidades de la empresa 1 serían expresadas así:
Esto requiere que la empresa 1 elija su nivel de producción en el punto en que el
ingreso marginal sea igual al costo marginal. La condición de para la maximización
de utilidades de la empresa 1 es:
13
Despejando
obtenemos la curva de reacción o función de mejor respuesta para la
empresa 1.
Bajo el supuesto que todas las empresas son idénticas ya que la solución del modelo
de Cournot es simétrica la función de reacción de cualquier empresa tiene la misma
estructura. Por lo tanto diremos:
Y en el equilibrio de Nash cada empresa elegirá la mejor respuesta que refleje la
predicción adecuada para las N-1 empresas.
Dado que cada empresa tiene iguales costos marginales se puede decir que su
producción en equilibrio será
por lo tanto podemos reemplazar
Por lo tanto podemos deducir que la producción de equilibrio Cournot – Nash será:
14
Para la industria:
;
Siguiendo nuestro análisis, tomemos a N =1 es decir una empresa estaríamos
hablando de un monopolio, si N=2 la producción es de un duopolio y si N va
aumentando en nuestra ecuación del precio, el termino
hasta desaparecer, mientras que el termino
se acercara a cero
se acercara a 1 lo cual significa
que el precio se llegara a igualar al costo marginal; obteniendo un resultado
característico de la competencia perfecta.
El modelo de Cournotmanifiesta que a medida que aumenta el número de empresas
homogéneas en el mercado el equilibrio converge al de competencia perfecta, ya que
cada empresa se hace más pequeña en relación al mercado.
1.2.
Modelo de Bertrand
A fin de simplificar, escogeremos el caso de un duopolio. El análisis se generalizara
de forma directa para el caso de “n” empresas. Supongamos que las empresas
venden bienes homogéneos, que son sustitutos perfectos en las funciones de utilidad
de los consumidores y que no existen restricciones de capacidad. (Tirole, 1988)
Las empresas fijan sus precios de manera simultánea. De tal manera que si las dos
empresas fijan el mismo precio se repartirán la demanda del mercado en partes
iguales. Si el precio de la empresa 1 es mayor que el de la empresa 2, la demanda
de la empresa 1 será 0. Si la empresa 1 fija un precio menor al de la empresa 2
obtendrá toda la demanda del mercado.
Aunque en la industria existen pocas empresas en este caso dos (duopolio), estas
empresas no tienen la capacidad para controlar el precio y aunque suene
contradictorio se puede entender si es que vemos esto más como una pugna por
15
ganar una mayor demanda a través de un concurso de precios, a esto se le conoce
como la paradoja de Bertrand.
Edgeworth encontró la solución a la paradoja de Bertrand introduciendo restricciones
de producción, con esto las empresas no pueden vender más de lo que producen.
Ahora supongamos que la empresa 1 tiene menor capacidad de producción que la
demanda del mercado, la empresa dos incrementa su precio de manera muy leve
entonces la empresa 1 no podrá satisfacer toda la demanda y los consumidores
tendrán que recurrir a la empresa 2 que tiene un precio mayor a su costo marginal
obteniendo un beneficio positivo.
“Las empresas que compiten en precios y venden productos idénticos rara vez
escogerán aumentar su capacidad para atender la demanda futura total del mercado
a precios competitivos”. (Pepall, 2006, p. 235).
Si tenemos el supuesto de que existe un “tiempo del juego”, es decir si dos empresas
tienen un mismo precio ligeramente por encima de su costo marginal y la empresa 1
decide bajar su precio, entonces se quedara con toda la demanda del mercado, pero
si introducimos ésta dimensión temporal la empresa 2 tendrá capacidad de reacción
y disminuirá su precio para no perder toda su demanda, ahora la empresa 1 tendrá
que comparar sus ganancias a corto plazo con sus pérdidas que se generarán por la
guerra de precios para determinar si le conviene seguir bajando su precio.
Supongamos que existe una diferenciación en el producto esto también sería una
solución a la paradoja de Bertrand. Por ejemplo dos empresas con el mismo bien o
servicio pero ubicados en diferentes lugares, la empresa 1 fija un precio igual a su
costo marginal y la empresa 2 un precio ligeramente mayor a su costo marginal,
existirá un costo de transporte a cada una de las empresas. Y aunque la empresa 2
tenga un precio más alto no significa que perderá toda su demanda ya que existirán
personas que vivan más cerca de su empresa y preferirán ir a la empresa 2 así el
precio sea más alto. La diferenciación del producto no siempre será la distancia,
dependerá del bien o servicio que se esté ofreciendo.
16
“Otra paradoja del modelo es que uno se puede preguntar por qué las empresas se
molestan en entrar al mercado si no obtienen ningún beneficio”. (Tirole 1988, p. 321)
Ahora supongamos que existe un costo fijo para entrar al mercado, entonces si una
empresa ingresa la otra no lo hará por más mínimo que sea este costo. Creándose
un monopolio.
En el grafico N°7 representamos la rivalidad de las empresas en el precio, estas que
reducirán sus precios para tratar de obtener una mayor demanda. Esta rivalidad hará
que las empresas bajen sus precios hasta sean iguales a sus costos marginales,
ninguna empresa tendrá un precio menor a su costo marginal porque esto le
generaría beneficios negativos. (Véase en anexos)
17
SECCION III: COMPETENCIA EN DOS ETAPAS
2.1. Modelo de Kreps-Scheikman: Rivalidad en dos Etapas
En 1983 los economistas Kreps y Scheikman plantearon un enfoque con el cual se
puede analizar de una manera más realista la conducta de las empresas
oligopólicas.
Supuestos
El capital es una variable de ajuste lento, en muchos casos no existe un ajuste rápido
según la función de demanda.
Los precios se pueden ajustar rápidamente.
Las capacidades de la firma son limitadas (restricciones de capacidad)
(Fernández-Baca, 2000)
Lo anterior nos lleva a un juego de 2 etapas, donde primero las empresas
seleccionan de forma simultánea sus capacidades, esto es“una elección de escala
que determinan las funciones de coste de la empresa y determina así las condiciones
para la competencia en precios” (Tirole, 1988, p.333).
La segunda etapa consiste precisamente en fijar los precios simultáneamente, dadas
las capacidades de los competidores. Las acciones del primer periodo son
denominadas estratégicas en la medida en que condicionen las acciones del
siguiente periodo (inversiones hundidas o irreversibles), las acciones del segundo
periodo o etapa se denominan tácticas. (Fernández-Baca, 2000)
El grafico N°8 muestra que los costes marginales son relativamente constantes,
hasta donde se agota la capacidad instalada, luego de ello el costo de la capacidad
es infinito.(Véase en anexos)
18
Si suponemos que los productos son homogéneos, la empresa que cobre un menor
precio va a satisfacer toda la demanda hasta su capacidad instalada y el resto que se
denomina demanda residual lo satisface la empresa que cobra mayor precio.
(Tarzijan, Jorge y Ricardo Paredes, 2006)
Lo anterior manifiesta una regla de racionamiento eficaz de los demandantes,
aquellos consumidores con menor disposición a pagar son servidos por la empresa
que cobre el menor precio, luego la otra empresa enfrenta una demanda residual y
sirve a los consumidores con mayor disposición a pagar, este racionamiento es
eficaz porque maximiza el excedente de los consumidores.
Para llegar al equilibrio, como se trata de un juego dinámico de dos etapas se
resuelve por inducción hacia atrás. Si supone que la empresa 1 realiza una inversión
“K” en el primer periodo, esto afecta sus costos en el segundo periodo, pero no así
los costos de la empresa 2. Se determina primero el equilibrio en el segundo periodo,
para cualquier valor de K, y luego se retrocede al primer periodo para determinar la
elección de K óptimo por parte de la empresa 1. (Fernández-Baca, 2000)
El resultado de este modelo es que en la primera etapa el nivel de producción que
maximiza ganancias es igual al equilibrio Nash-Cournot, luego las empresas
determinan su capacidad de producción sobre la base de las cantidades que resultan
de dicho equilibrio.Dada la capacidad máxima de planta, determinada por el nivel de
producción Nash-Cournot, las empresas rivalizan en precios pero con las
restricciones de capacidad Nash-Cournot, con lo que el resultado en términos de
precios, en la segunda etapa, es el de un equilibrio Nash-Cournot, en precios y
cantidades. (Pérez-Reyes, 2006)
Al margen de si la competencia se desata vía cantidad (Cournot) o vía precios
(Bertrand), es importante analizar si las pendientes de la función de reacción es
positiva o negativa según la variable en que se compita, en el caso del equilibrio de
Nash- Cournot las pendientes de las funciones de reacción son negativas por el
hecho de que si la empresa 1 decide aumentar su producción, la empresa 2 se
enfrentara a un precio más bajo y por ello sus beneficios brutos disminuirán. Por otra
19
parte la solución de equilibrio de Bertrand con bienes diferenciados da como
resultado funciones de reacción con pendientes positivas, esto denota que si la
empresa 1 baja su precio, la empresa 2 se ve incentivada a hacer lo mismo para no
perder mercado o disminuir sus beneficios brutos.
Por último es necesario acotar que en la realidad algunos mercados se representan
mejor con el modelo de Cournot, en el sentido de que la restricción de capacidad es
la decisión relevante, así tenemos a la industria de cemento, acero, autos,
computadoras, las plantas de generacióneléctrica donde estas tienen al limite su
capacidad de producción por cierto número de años. En el modelo de Bertrand la
capacidad no es restricción, así tenemos el mercado de seguros o de programa de
software, no obstante debe hacerse uso de la econometría para convalidar la forma
en que compiten las empresas. (Notas de organización industrial 1, 2011)
2.2. Modelo de Stackelberg
El modelo de oligopolio de Stackelberg (1934) es un caso de juego en dos etapas en
el que los conjuntos de acciones desarrolladas por las empresas son continuas.
Pepall et al (2006) nos indica, “a diferencia de los juegos simultáneos, como los
modelos tradicionales de Bertrand o Cournot, que describen una interacción primera
y única en el mercado de las empresas rivales” (P.248).
Los jugadores son dos empresas que conforman un duopolio; estas empresas tienen
productos homogéneos, una de estas dos será la empresa líder quien decide su
producción en primer lugar, y la otra empresa será la seguidora quien está a la
espera de la decisión de la empresa líder para elegir su producción; tiene cierta
similitud con el modelo de Cournot; el cual lo toma como base.
“La elección secuencial de producción es lo que hace que el juego sea dinámico. Sin
embargo, las empresas se reúnen sólo una vez y su interacción lleva a un resultado
de una vez por todas de liquidación del mercado”. (Pepall, 2006, p. 248)
20
“Si las variables estratégicas son los precios, significaría que las empresas
seguidoras fijan sus precios en respuesta a la iniciativa de la empresa líder, y esta
elige sus precios sabiendo que las seguidoras ajustarán posteriormente sus precios
de una manera predecible”. (Fernández Baca, 2000, p. 222)
2.2.1. Equilibrio de Stackelberg
Suponemos que la empresa 1 sabe que la empresa 2 se comporta como un
duopolista de Cournot; ambas empresas son racionales y estratégicas.
Representaremos la demanda a través de una función lineal de la demanda
inversa
.
Cada empresa tiene el mismo costo unitario de producción .
La producción total de la Industria es igual a la suma de producciones de cada
empresa
La empresa 1 actúa primero para elegir
,
tomando en cuenta la función de
reacción de la empresa 2 (función de respuesta de la empresa 2 para cada
valor de
.
Solución de primer orden:
21
Luego se escoge la opción de
, la cual dada la función de respuesta de la
empresa 2 a ese nivel de producción da como resultado la maximización de
utilidades de la empresa 1.
Función utilidad:
Al actuar primero la empresa 1 gana la capacidad de manipular la elección del
nivel de producción de su rival. Despejamos condiciones de primer orden para
la maximización de utilidad; derivamos IT e igualamos a cero.
22
Si comparamos estos resultados con Cournot en los cuales los resultados
serian los siguientes
; esto se visualiza
mejor en el grafico N°9.(Véase en anexos)
2.2.2. Resultados
 El líder obtiene mejores resultados que en el modelo de Cournot, ya
que es el que manipula estratégicamente la conducta del seguidor,
motivo por el que éste obtiene peores resultados.
 La cantidad total
en el equilibrio de Stackelberg es superior a la
cantidad total en el equilibrio de Cournot.
 En el equilibrio
de Stackelberg la empresa 1 produce más
y la
empresa 2 produce menos que en el equilibrio de Cournot, pero el
aumento de la empresa 1 es mayor que el descenso de la empresa 2.
 En el equilibrio
de Stackelberg la empresa 1 produce más
y la
empresa 2 produce menos que en el equilibrio de Cournot, pero el
aumento de la empresa 1 es mayor que el descenso de la empresa 2.
 En el equilibrio
de Stackelberg la empresa 1 produce más
y la
empresa 2 produce menos que en el equilibrio de Cournot, pero el
aumento de la empresa 1 es mayor que el descenso de la empresa 2.
 En cuanto a la producción total y el precio de mercado se obtiene una
producción mayor a la del equilibrio de Cournot y un precio menor.
23
SECCION IV: EJERCICIO DE APLICACIÓN
Suponga que el servicio de telefonía celular es asegurado por dos empresas:
Teleagónica (firma 1) y el Belt Down (firma 2) las cuales ofrecen un servicio móvil
homogéneo en el área. La demanda de servicios de telefonía celular es dada por la
función
y que ambas firmas tienen la misma función de costo, sea
a) Suponga que la firma 1 se comporta a lo Cournot con respecto a la firma 2. Dado
el output
de la firma 2 determine la curva de demanda residual de la firma 1.
Determine la función de mejor respuesta de la firma 1 para el nivel de output elegido
por la firma 2.
24
…..F.R.1
……F.R.2
b) Suponga que ambas firmas compiten ahora como duopolistas tipo Cournot.
Encuentre la función de mejor respuesta de la firma 2 al output de la firma 1. Utilice la
función de mejor respuesta de la pregunta a) para calcular el equilibrio de CournotNash de precios y cantidades. Use estos resultados para calcular los beneficios de
cada una de las firmas.
……F.R.2
Reemplazando en F.R.1
25
c) Retorne al caso original en donde no hay costos fijos y suponga que ambas firmas
elegirán precios como lo sugiere Bertrand. Halle el precio de equilibrio, el output y
beneficios de cada firma.
d) Hallar el equilibrio de Stackelber
…..F.R.2
26
El grafico N° 10 correspondiente al ejercicio se muestra en los anexos.
27
V. CONCLUSIONES
 La teoria de juegos ofrece un marco teórico de analisis de gran ayuda para
comprender las estrategias en competencia oligopólica. El equilibrio de Nash
permite eliminar ciertas combinaciones pero en algunos casos no permite
encontrar un resultado único, por ello se debe considerar otros factores como
la experiencia previa y el aprendizaje.
 El modelo de Cournot manifiesta que a medida que aumenta el número de
empresas homogéneas en el mercado el equilibrio converge al de
competencia perfecta, ya que cada empresa se hace más pequeña en
relación al mercado.
 En un equilibrio de Bertrand las empresas fijan un precio igual al CMg,
compiten en precios y se obtiene el resultado de competencia perfecta, para
mas de unaempresa en el mercado. A esto se le conoce como la Paradoja de
Bertrand.
 A corto plazo el equilibrio de Stackelberg presenta un mejor beneficio; a
comparación del equilibrio de Cournot; esto sucede ya que el precio en
Stackelberg es relativamente menor y su cantidad es mayor que en equilibrio
el de Cournot .A largo plazo cada vez habran consumidores con menores
ingresos; el precio de Stackelberg ira disminuyendo hasta alcanzar el costo
marginal lo cual resultara que obtendrá menos ganancias que en el equilibrio
de Cournot
 El
modelo
de
Kreps-Scheikman
ofrece
un
analisismas
realista
del
comportamiento de las empresas. El resultado de este analisises el de un
equilibrio Nash-Cournot, en precios y cantidades.
28
 En la realidad algunos mercados se representan mejor con el modelo de
Cournot, por ejemplo en el caso delas plantas de generación eléctrica, otros
mercados tienen como mejor marco teorico los modelos de Bertrand,
Stackelberg o Kreps- Scheikman, es por ello que tener disponible varios
modelos de oligopolio es ventajoso para analizar casos particulares.
REFERENCIAS
Antúnez, C. (2010). “Modelos de Oligopolio en la Economía”. Disponible en.
http://findebookee.com/m/modelos-oligopolio-economia
Contreras, A. (2010). “Modelos de mercado de Stackelber para múltiples
líderes y seguidores”: Formulación, resolución y aplicación. Disponible en.
http://www.iit.upcomillas.es/pfc/resumenes/4df500e58f0a0.pdf
Fernández-Baca, J. (2000). Microconomía: Teorías y aplicaciones Tomo II.
Lima: Universidad del Pacífico- Centro de Investigacion
León, M; Fernández, A. (2008). “Oligopolios: Modelo de Stackelberg”.
Disponible en. http://rodin.uca.es:8081/xmlui/handle/10498/6876
Ortiz, A. (2005) Manual y ejercicios corregidos de Microeconomía Lima:
Fondo editorial Departamento de Economía y Planificación - Universidad
Nacional Agraria La Molina
Osório, C; Maca, P. (2002). La determinación de los precios de bienes
durables
en
duopolio.
Disponible
en.
http://econpapers.repec.org/paper/wpawuwpmi/0202004.htm
Pepall, L. , Richards, D. , Norman G. (2006). Organización industrial teoría y
práctica contemporánea. mexico: International TomsonLearning.
Revilla, J. (1996). “Un modelo Stackelberg del mercado bancario en
Nicaragua: El caso de la banca estatal y su impacto en la determinación de la
29
tasa de interés”. Disponible en.
http://www.bcn.gob.ni/publicaciones/eventuales/investigaciones/documentos_t
rabajo/DT-1-1996.pdf
Reyes,
E.
(2006).
“Practicas
Competitivas”.
Disponible
en.
http://www.ariae.org/pdf/IV_CursoRegulacionEnergeticaAriae/PDF_N14_N15_
PracticasCompetitivas.pdf
Tarzijan, J. y Paredes, R. (2006). Organización industrial para la estrategia
empresarial. Mexico. Pearson Educación
Tirole, J. (1988). Teoría de la organización industrial. Barcelona. Ariel
Varian, H. (1999).Microeconomía Intermedia: un enfoque actual. Barcelona:
Antoni Boch.
Zipitria, L. (2011). “Notas de organización industrial”. Disponible en.
http://leandrozipitria.files.wordpress.com/2008/12/cursooi-2011.pdf
30
ANEXOS
31
Grafico N°1: Matriz de pagos de horarios
American
Delta
Mañana
Tarde
Mañana
(15; 15)
(30; 70)
Tarde
(70; 30)
(35; 35)
Fuente: Pepall, 2006
32
Grafico N°2: Matriz de pagos de utilidades
American
Delta
Pa
Pb
Pa
(9000; 9000)
(0; 3600)
Pb
(3600; 0)
(1800; 1800)
Fuente: Pepall, 2006
33
Gráfico Nº3: Curvas de Reacción en el Modelo de Cournot
q2
R1
q *2
R2
q1
q *1
Fuente: Pepall, 2006
34
Gráfico Nº 4: Interacción de las empresas
P, CMg
CMg
P(Q)
D3
D2
Fuente: Pérez Reyes 2006.
35
D1
D0
q1
GRAFICO Nº5- Curva de reacción de la empresa 1
q2
qCP2
q12
q02
R1
q 11
q01 qM1
q1
Fuente: Pérez Reyes, 2006
36
Gráfico N°6- Equilibrio Nash-Cournot
q2
q *2
R2
q *1
q1
Fuente: Pérez Reyes, 2006
37
GRAFICO N°7: Equilibrio de Bertrand
Fuente: Pérez Reyes, 2006
38
Grafico N°8 : Costes marginales
Cmg
Cmg(Q)
k
Q
Fuente: Documents & Resources for Small Businesses & Profesionals, 2008
39
Grafico Nº 9: Comparación de los resultados de Cournot y Stackelberg
Fuente: Pepall, 2006
40
Grafico N° 10: Equilibrio de Cournot, Bertrand y Stackelberg
q1
12
FR1
BERTRAND
D
6
COURNOT
4
STACKELBER
3
4
6
Fuente: Ortiz, 2005
41
12 q2