PROYECCIONES PERPENDICULARES Y SIMÉTRICOS (Pág 124

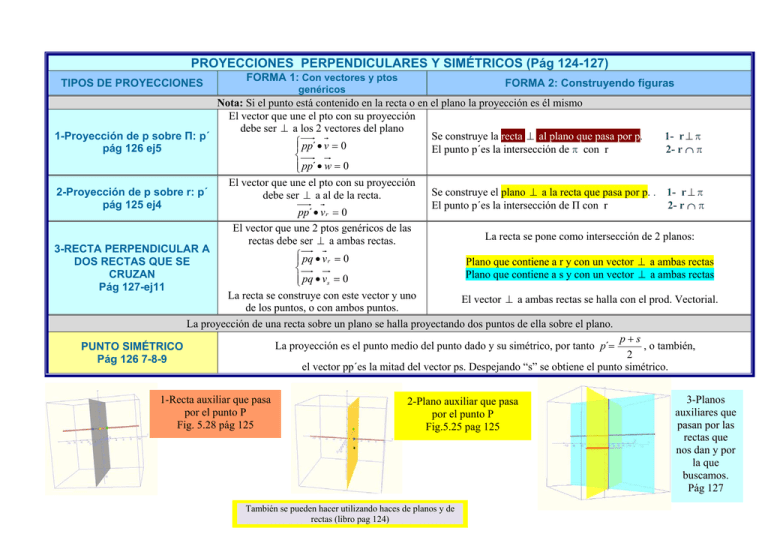
25/04/2011
PROYECCIONES PERPENDICULARES
Y SIMÉTRICOS (Pág 124-127)
TIPOS DE PROYECCIONES
FORMA 1: Con vectores y ptos
FORMA 2: Construyendo figuras
genéricos
Nota: Si el punto está contenido en la recta o en el plano la proyección es él mismo
El vector que une el pto con su proyección
debe ser ⊥ a los 2 vectores del plano
Se construye la recta ⊥ al plano que pasa por p.
1- r ⊥ π
1-Proyección de p sobre Π: p´
⎧⎪ pp´ • v = 0
pág 126 ej5
El punto p´es la intersección de π con r
2- r ∩ π
⎨
⎪⎩ pp´ • w = 0
El vector que une el pto con su proyección
Se construye el plano ⊥ a la recta que pasa por p. . 1- r ⊥ π
2-Proyección de p sobre r: p´
debe ser ⊥ a al de la recta.
pág 125 ej4
El punto p´es la intersección de Π con r
2- r ∩ π
pp´ • v r = 0
El vector que une 2 ptos genéricos de las
La recta se pone como intersección de 2 planos:
rectas debe ser ⊥ a ambas rectas.
3-RECTA PERPENDICULAR A
⎧⎪ pq • v r = 0
Plano que contiene a r y con un vector ⊥ a ambas rectas
DOS RECTAS QUE SE
⎨
Plano que contiene a s y con un vector ⊥ a ambas rectas
CRUZAN
⎪⎩ pq • vs = 0
Pág 127-ej11
La recta se construye con este vector y uno
El vector ⊥ a ambas rectas se halla con el prod. Vectorial.
de los puntos, o con ambos puntos.
La proyección de una recta sobre un plano se halla proyectando dos puntos de ella sobre el plano.
p+s
La proyección es el punto medio del punto dado y su simétrico, por tanto p´=
, o también,
PUNTO SIMÉTRICO
2
Pág 126 7-8-9
el vector pp´es la mitad del vector ps. Despejando “s” se obtiene el punto simétrico.
1-Recta auxiliar que pasa
por el punto P
Fig. 5.28 pág 125
2-Plano auxiliar que pasa
por el punto P
Fig.5.25 pag 125
También se pueden hacer utilizando haces de planos y de
rectas (libro pag 124)
3-Planos
auxiliares que
pasan por las
rectas que
nos dan y por
la que
buscamos.
Pág 127