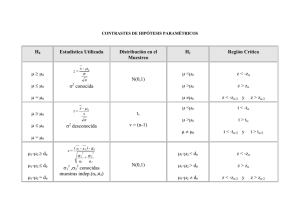
9.5.4. Contrastes de la razón de varianzas

234
Bioestadı́stica: Métodos y Aplicaciones


 H0 : µ1 − µ2 = 0

 H : µ − µ 6= 0
1
1
2
9.5.4.
Contrastes de la razón de varianzas
Consideramos dos muestras independientes de dos poblaciones que se
distribuyen normalmente (cuyas medias y varianzas son desconocidas). Vamos a abordar cuestiones relacionadas con saber si las varianzas de ambas
poblaciones son las mismas, o si la razón (cociente) entre ambas es una
cantidad conocida, R. La igualdad entre las dos varianzas puede escribirse
σ12 − σ22 = 0 o bien, la existencia de una diferencia entre ambas (∆), del
modo σ12 − σ22 = ∆. Este modo de escribir la diferencia entre varianzas (que
era el adecuado para las medias) no es sin embargo fácil de utilizar para las
varianzas, de modo que nos será más fácil sacarle partido a las expresiones
de las relaciones entre varianzas como
σ12
= R.
σ22
Por ejemplo, si R = 1 tenemos que ambas varianzas son iguales.
Consideramos entonces la hipótesis nula
H0 :
σ12
=R
σ22
la cual vamos a contrastar teniendo en cuenta que:
(n1 − 1) Ŝ12
;χ2n1 −1
σ12
(n2 − 1) Ŝ22
;χ2n2 −1
σ22







1
(n1 −
\ 1) Ŝ12
σ22 Ŝ12
(n1 −
\ 1)
σ12
=⇒
=
;Fn1 −1,n2 −1

σ12 Ŝ22
1
(n2 −
\ 1) Ŝ22





(n2 −
\ 1)
σ22
9.5. CONTRASTES DE DOS DISTRIBUCIONES NORMALES INDEPENDIENTES 235
Por tanto el estadı́stico del contraste que nos conviene tiene una distribución
conocida cuando H0 es cierta —véase la definición de la distribución de
Snedecor:
F =
1 Ŝ12
;Fn1 −1,n2 −1
R Ŝ22
Contraste bilateral
El contraste bilateral para el cociente de varianzas se escribe como:

σ12



H
:
=R
0


σ22




σ12


6 R
 H1 : 2 =
σ2
Habida cuenta que la distribución F de Snedecor no es simétrica sino que
sólo toma valores positivos, se rechazará la hipótesis nula cuando el el valor
que tome el estadı́stico del contraste al aplicarlo sobre una muestra sea
muy cercano a cero, o bien, muy grande. Es decir, se define el estadı́stico
experimental y los lı́mites de la región crı́tica como:
Fexp =
1 Ŝ12
R Ŝ22
ateo = Fn1 −1,n2 −1,α/2
bteo = Fn1 −1,n2 −1,1−α/2
y el criterio de aceptación o rechazo es:



si ateo ≤ Fexp ≤ bteo

 si F
exp < ateo ó Fexp > bteo
=⇒
no rechazamos H0 ;
=⇒
rechazamos H0 .