Hidráulica de captaciones

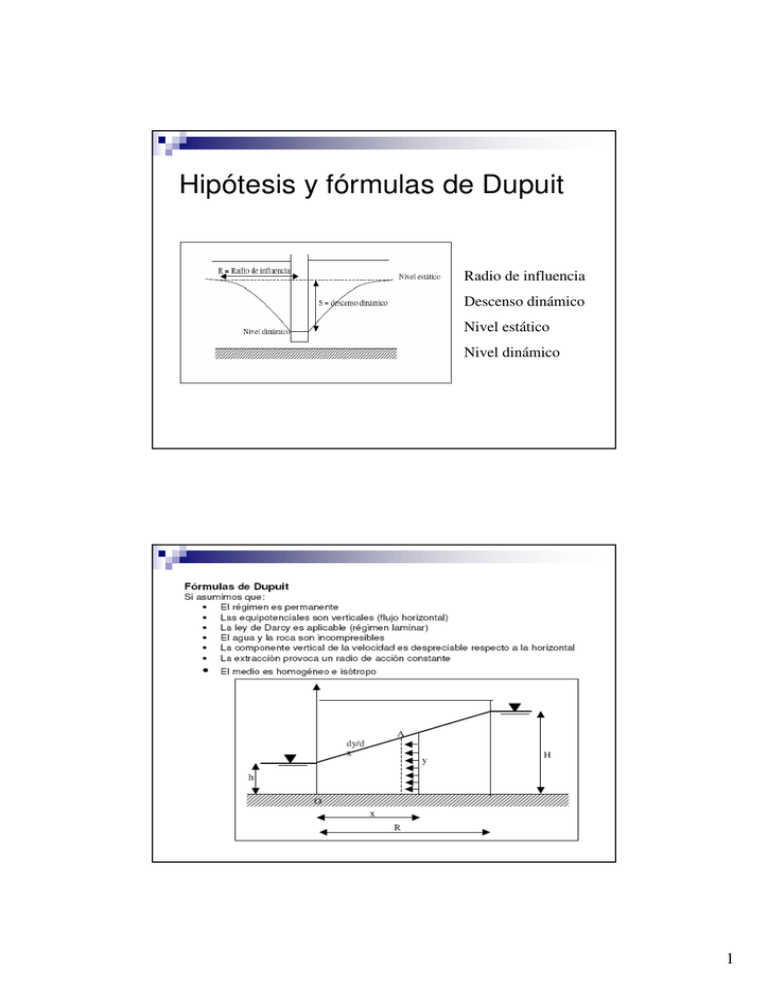
Hipótesis y fórmulas de Dupuit
Radio de influencia
Descenso dinámico
Nivel estático
Nivel dinámico
1
•
•
•
•
•
•
En una dimensión
Sección A = ly
Gradiente dy/dx
Q = K l y dy/dx
Para x=0 y=h
Para x=R y=H
Ecuación de la parábola de Dupuit
•
•
•
•
•
En tres dimensiones
Suponemos un cilindro de radio r alrededor del pozo en
una isla circular de radio R. La superficie de flujo de
agua hacia el pozo es A=2πry
Gradiente dy/dx
Q = K l y dy/dx
Para x=r y=h
Para x=R y=H
Que es la curva de Dupuit, que define el conoide de
depresión
2
Hidráulica de captaciones.
Ecuación general del flujo subterráneo.
Se deriva de la aplicación de la Ley de Darcy y del teorema de la continuidad o de
la conservación de la masa
∂ 2 h ∂ 2 h ∂ 2 h F S ∂h
+
+
+ =
∂x 2 ∂y 2 ∂z 2 K T ∂t
Suma de entradas
y salidas de agua
Recargas de agua
Variación del
almacenamiento
h = potencial hidráulico (nivel piezométrico)
F = recargas exteriores (verticales, lluvias, etc..)
K = conductividad hidráulica del acuífero
S = coeficiente de almacenamiento
T = transmisividad
t = tiempo
Si no existen recargas exteriores
F/K = 0
Si el flujo es radial y no existe
componente respecto al eje Z
∂ 2h
=0
∂z 2
Si el régimen es permanente
S ∂h
=0
T ∂t
La ecuación queda:
∂ 2h ∂ 2h
+
=0
∂x 2 ∂y 2
3
Caudal específico
Caudal por unidad de descenso, l/s/m
Caudal crítico, representaría un caudal máximo para
mínimo descenso (a partir de este punto con pequeños
incrementos de caudal, se producen importantes
descensos)
ENSAYOS DE BOMBEO
Q
R
x
hs
∆s
b
piezómetro
curva de
depresión
h
Q Caudal
R radio de influencia
R radio del pozo
X distancia al piezómetro
B espesor del acuífero
s descenso dinámico (depresión)
hs nivel dinámico
línea equipotencial
4
Respecto al pozo, informan sobre:
Calidad de la construcción (eficiencia del pozo)
Pérdidas de carga
Caudal de bombeo más aconsejable
Colocación de la bomba
Respecto al acuífero, informan sobre:
Transmisividad y conductividad hidráulica
Coeficiente de almacenamiento
Existencia de barreras o bordes impermeables
Zonas de recarga
Área del embalse subterráneo
Otros elementos
Radio de influencia del sondeo
Amplitud de la zona de llama (perímetros de protección)
Métodos de ensayo
• A caudal constante
Régimen de equilibrio (permanente), los niveles no
varían con el tiempo
Régimen no permanente, los niveles varían con el
tiempo
• A caudal variable
Bombeo a caudal crítico
Bombeos escalonados
• Ensayos de recuperación
5
Métodos de ensayo a caudal constante
Tipo de acuífero
Tipo de ensayo
Régimen permanente
Confinado
Régimen variable
Prueba en
descensos
Fórmula de Theis
Recuperación
Fórmula de recuperación de Theis
Régimen permanente
Semiconfinado
Régimen variable
Método de análisis
Fórmula de Thiem
Descensos
Recuperación
Régimen permanente
Aproximación logarítmica de Jacob
Fórmula de De Glee o de Jacob-Hantush
Fórmula de Hantush
Estudio de ascensos teóricos (1)
Fórmula de Thiem (2) y corrección de Jacob
Fórmula de Dupuit (3)
Fórmula de Theis (4)
Libre
Régimen variable
Prueba en
descensos
Aproximación logarítmica de Jacob (4)
Corrección de Dupuit
Fórmula de Boulton
Fórmula de Neuman
Recuperación
Fórmula de recuperación de Theis (2)
(1) Si el bombeo es lo suficientemente largo como para que los niveles se estabilicen, los ascensos
teóricos coinciden con los medidos
(2) Si los descensos son pequeños en comparación con el espesor saturado del acuífero
(3) Admitiendo la aproximación de Dupuit-Forchheimer
(4) Si los descensos son pequeños en comparación con el espesor saturado del acuífero y si el drenaje
es instantáneo y proporcional al descenso producido (no existe drenaje diferido)
METODOS EN RÉGIMEN PERMANENTE
• El nivel permanece invariable o prácticamente
invariable después de un cierto tiempo de
bombeo o de estabilización
• El término
S ∂h
T ∂t
se considera nulo
• El S no puede calcularse
• Se determina la transmisividad (datos del pozo
de bombeo), radio de influencia y pérdidas de
carga (si hay piezómetros)
6
Acuíferos confinados. Método de Thiem
d1 − d 2 =
Q
r
ln 2
2πT r1
d1 − d 2 = 0.366
Q r2
lg
T r1
d1 depresión producida por le bombeo en el piezómetro 1
d2 depresión producida por le bombeo en el piezómetro 2
Q caudal de bombeo (cte)
T Transmisividad
r1 distancia del pozo de bombeo al piezómetro 1
r2 distancia del pozo de bombeo al piezómetro 2
d p − d 2 = 0.366
Q r2
lg
T rp
d p = 0.366
d p = 0.366
Q R
lg
T rp
Q R
lg
T rp
Acuíferos confinados. Método de Thiem
(Procedimiento gráfico)
∆d
d i = 0.366
Descensos (m)
(r1, d1)
(r2, d2)
∆d10
(r3, d3)
d i = 0.366
(r4, d4)
y=
(r5, d5)
1
101
102
Distancia (m)
103
104
m
Q R
lg
T ri
Q
Q
lg ri + 0.366 lg R
T
T
x +
n
Q
m = 0.366
T
R
∆y
∆d
m=
=
∆x ∆ lg r
m = ∆d
T = 0.366
Q
∆d
R , representado por el punto de corte de la recta con las el eje de abscisas, d=0
El valor (rpdp) puede salirse de la recta ajustada debido a pérdidas de carga. La diferencia
entre dp teórica y dp real mediría el valor de las pérdidas de carga.
Si el rp es inferior a 1 metro, habría que extrapolar los valores a otro ciclo logarítmico
7
EJERCICIO
En un sondeo de radio 0,3 m situado en un acuífero confinado, se ha realizado un
ensayo de bombeo a un caudal de 3300 l/min llegando a estabilizarse los niveles. En el
sondeo se midió un descenso de 15 m. En tres piezómetros de observación se
observaron los descensos indicados en la tabla siguiente:
Piezómetro
Distancia al pozo de bombeo (m)
Descenso (m)
P-1
10
6,80
P-2
40
4,70
P-3
110
2,90
A partir de los datos obtenidos de diferentes sondeos, se ha podido estimar un espesor
medio de 55 m de formación permeable.
a) Calcular la transmisividad y conductividad hidráulica del acuífero y el radio de
influencia
b) Calcular el descenso teórico en el sondeo
c) ¿Qué caudal específico presenta este sondeo?. ¿Cuál sería el caudal específico si no
existiesen pérdidas de carga?
d) Calcular el descenso teórico producido en el sondeo y en los piezómetros si se
bombease un caudal de 2580 m3/día. ¿Podría determinarse el descenso real?. ¿Qué
descenso se produce a 1650 m de distancia del punto de bombeo?
Calcular la transmisividad y la conductividad hidráulica del
acuífero y el radio de influencia
Apartado a
T = 0.366
Q
4752 m 3 / día
= 0,366
= 561m 2 / día
∆d
3,1m
T 561m 2 / día
K= =
= 10, 2m / día
b
55 m
R = 1500 m
Descensos (m)
20
15
10
5
0
0,1
1
10
100
1000
10000
Distancia (m)
8
Apartado b
Calcular el descenso teórico en el sondeo
d t = d p − ∆d = 15 m − 3,8m = 11,2 m
Apartado c ¿Qué caudal específico presenta este sondeo?.
¿Cuál sería el caudal específico si no existiesen pérdidas de carga?
qe =
Q 4752 m 3 / día
=
= 3,7l / seg / m
sp
15 m
qe =
Q 4752 m 3 / día
=
= 4,91l / seg / m
dt
11, 2m
Apartado d Calcular el descenso teórico producido en el sondeo y
en los piezómetros si se bombease un caudal de 2580 m3/día.
¿Podría determinarse el descenso real?.
¿Qué descenso se produce a 1650 m de distancia del punto de bombeo?
d = 0.366
Q R
lg
T r
d s = 0.366
2580 m 3 / día 1500 m
lg
= 6,23m
561m 2 / día
0,3m
d1 = 0.366
2580 m 3 / día 1500 m
lg
= 3,66 m
561m 2 / día
10 m
d 2 = 0.366
2580 m 3 / día 1500 m
lg
= 2,65 m
561m 2 / día
40 m
d 3 = 0.366
2580 m 3 / día 1500 m
lg
= 1,91m
561m 2 / día
110 m
9
Acuíferos libres. Corrección de Dupuit
El flujo no es radial y por lo tanto, estas líneas se distorsionan dando
componentes verticales
Para solucionarlo, se hace una corrección de los descensos y se aplica la
fórmula de Thiem
d2
dc = d −
2H 0
H espesor saturado inicial del acuífero
0
No es necesario hacer la corrección ciando el descenso observado sea menor de
un 10 o 15% del espesor saturado inicial H0.
Aproximación a la transmisividad
A partir de la formula de Thiem y considerando un valor de R=700 m y rp= 0.5 m
T (m / día) = 100 ⋅
Q(l / s )
d p ( m)
Ejercicio
Se ha realizado un ensayo de bombeo en un acuífero libre hasta alcanzar
el régimen estacionario, habiéndose obtenido los siguientes descensos. En
el pozo, con una radio de 0.28 m, el descenso es de 8.0 m. En los cuatro
piezómetros de observación se observaron los descensos indicados en la
tabla siguiente:
Piezómetro
Distancia al pozo de bombeo (m)
Descenso (m)
P-1
10
4.8
P-2
25
3.4
P-3
60
2.0
P-4
100
1.3
a) Calcular la conductividad hidráulica del acuífero si el caudal de bombeo fue de 60
m3/hora. El espesor saturado inicial del acuífero era de unos 20 metros.
b) Establecer el radio de influencia
c) Comentar si era necesaria la corrección y comparar resultados con dicha corrección
efectuada y sin efectuar
d) Calcular la transmisividad inicial
10
Apartado a) Calcular la conductividad hidráulica del acuífero si el caudal
de bombeo fue de 60 m3/hora. El espesor saturado inicial del acuífero era
de unos 20 metros.
Descenso
Des. Corregido
Logarítmica (Descenso)
Logarítmica (Des. Corregido)
6
5
4
3
2
1
0
1
10
100
1000
Dist ancia (m)
Q
1440 m 3 / día
K = 0.366
= 0,366
= 7.3m / día
H 0 ∆d
20 m 3,6m
K = 0.366
Q
1440 m 3 / día
= 0,366
= 8.8m/ día
H 0 ∆d c
20 m 3,0 m
Apartado b) Establecer el radio de influencia
R = 250 m
Apartado c) Comentar si era necesaria la corrección y comparar resultados con
dicha corrección efectuada y sin efectuar
Es apreciable el error que se comete al tomar para los descensos el valor sin
Corregir
Apartado d) Calcular la transmisividad inicial
T= Kb
T= 8.8 m/día 20 m = 176 m2/día
11
Campo de aplicación
Estos métodos requieren pocos datos
Proporcionan escasa información
No permiten calcular S
Su principal ventaja es que se puede determinar
la transmisividad de manera rápida y sencilla.
METODOS EN REGIMEN VARIABLE
•
No se interpreta el descenso total sino la evolución de los niveles a
lo largo de la prueba.
•
El término S/T dh/dt de la ecuación general no se anula.
•
Metodología práctica: Se mide, en primer lugar, los niveles en el
pozo y en los piezómetros. Se arranca la bomba y se mide la
evolución de los niveles con el tiempo, con una cadencia que
reparta lo más uniformemente posible en una escala logarítmica
(1,2,3,4,5,6,8,10,12,15,25,30,40,50,60,80,100,150 y 180 minutos
para las tres primeras horas, después se mide a intervalos
sucesivos de 40, 50 minutos, 1, 2, 4 horas).
•
Al pararse la bomba, debe medirse los ascensos con una cadencia
análoga, lo que permitirá interpretar el ensayo de recuperación
12
ACUÍFERO CAUTIVO. METODO DE THEIS
d=
Q
4πT
∞
u
e −u
Q
du =
W (u )
u
4πT
r 2S
u=
4Tt
Q=
4πTs p
W (u p )
T=
QW (u )
4πd
S=
4Ttu
r2
R = 1 .5
Tt
S
d = descenso en un punto situado a una distancia r del punto de bombeo
Q = caudal
T = transmisividad
W(u) = función del pozo (tabulada, graficada)
S = coeficiente de almacenamiento
t = tiempo transcurrido a partir del inicio del bombeo
u = función auxiliar
EJERCICIO
Calcular los descensos de un pozo de 0.60 m de diámetro a 10 y 100 metros
del mismo a 1 hora y 1 día de iniciado el bombeo sabiendo que el caudal
constante de bombeo es de 100 m3/hora, la transmisividad del acuífero es de
1000 m2/día y el coeficiente de almacenamiento es de 10-4.
d=
u=
100 m 3 / h 24 h
W (u ) = 0.191W (u )
4π 1000 m 2 / día
2
r 2S
r 2 10 −4
−8 r
=
=
2
.
5
⋅
10
4Tt 4 1000 m 2 / día t
t
Estando r en m y t en días
13
Datos obtenidos a partir de las tablas de W(u) (función del pozo)
r
r (m)
t
u
W(u)
S(m)
Pozo
0.3
1 hora
1día
5.4.10-8
2.2.10-9
16.16
19.35
3.09
3.70
10
1 hora
1día
6.0.10-5
2.5.10-6
9.14
12.32
1.74
2.35
100
1 hora
1día
6.0.10-3
2.5.10-4
4.54
7.72
0.80
1.47
1000
1 hora
1día
0.6
2.5.10-2
0.45
3.14
0.086
0.600
EJERCICIO
¿A qué caudal máximo debe bombearse un pozo en un acuífero cautivo para
que al cabo de 1 mes de bombeo interrumpido el descenso teórico no supere
12 metros?. El radio del pozo es de 0.3 m, y la T= 200 m2/día y S = 5 .10-3.
2
0.32 m 2 5.10 −3
up =
=
= 1.88 .10 −8
2
4Tt 4 .200 m / día 30 días
rp S
W (u ) = 17 .21
Q=
4πTs p
W (u p )
=
4π 200 m 2 / día 12 m
= 1752 m 3 / día = 73m 3 / hora
17 .21
14
Función W(u) de pozo en acuífero confinado (Curva de Theis)
104
105
106
107
108
W (u)
101
100
100
101
102
103
10-1
104
1/u
Descensos, en metros
Curva de campo descensos - tiempo
101
100
100
101
102
103
10-1
104
Tiempo de bombeo, en minutos
15
Método de Brown. Procedimiento gráfico por superposición de la
curva-patrón de Theis y la curva descensos-tiempo
log t
log d
B
log W(u)
W(u)
d
t
A
1/u
log 1/u
Permite el cálculo de T y S
SIMPLIFICACIÓN DE JACOB
W (u ) ≈ ln
Si u< 0,1
d=
Si
Q
ln 2 ,r252 STt
4πT
r 2S
= t0
2,25Tt
d = 0,183
d = 0,183
0,562
u
Q 2,25Tt
lg 2
T
r S
t0 = punto de corte de la recta con el eje X
Q
Q
lg t − 0,183 lg t0
T
t
m = ∆d10 = 0,183
Q
T
16
10
9
8
Punto de corte = t0
Descenso en el pozo, en metros
11
7
6
5
4
3
Recta de Jacob
∆d10 = 0,183 (Q/T)
2
1
0
100
101
102
104
103
Descenso en el piezómetro, en metros
Tiempo de bombeo, en minutos
Recta ajustada
Periodo de
validez de Jacob
Periodo de no
validez de Jacob
t*
1
1
t0 10
102
103
104
Tiempo de bombeo, en minutos
17
EJERCICIO
Calcular los descensos de un pozo de 0.60 m de diámetro a 10 y 100 metros
del mismo a 1 hora y 1 día de iniciado el bombeo sabiendo que el caudal
constante de bombeo es de 100 m3/hora, la transmisividad del acuífero es de
1000 m2/día y el coeficiente de almacenamiento es de 10-4. Utilizar la
simplificación de Jacob
d = 0,183
Q 2,25Tt
t
lg 2
= 0.44 lg 2.25 ⋅10 7 2
T
r S
r
r (m)
t
S(m)Theis
S(m) Jacob
Pozo
0.3
1 hora
1día
3.09
3.70
3.09
3.69
10
1 hora
1día
1.74
2.35
1.75
2.35
100
1 hora
1día
0.87
1.47
0.87
1.47
1000
1 hora
1día
0.086
0.600
Absurdo
0.600
Más coincidentes cuanto cuanto mayor es el tiempo y/o menor la distancia al pozo de bombeo
EJERCICIO
La tabla corresponde a un ensayo de bombeo en un acuífero cautivo realizado
con un caudal constante de 100 l/sg en un pozo de 0.4 m de diámetro. Calcular
T y S. Los piezómetros P1 y P2 se encuentra a 10 metros y 100 metros,
respectivamente.
t(mto)
Sp1
Sp2
Spozo
1
3
6
10
20
40
70
100
200
400
700
1000
2000
3000
3.40
4.20
4.80
5.08
5.60
6.05
6.40
6.65
7.10
7.50
7.90
8.25
8.70
8.90
0.53
1.10
1.55
1.92
2.35
2.90
3.10
3.48
3.90
4.40
4.80
5.08
5.50
5.90
17.50
18.20
19.00
19.40
19.90
20.30
30.70
21.10
21.30
21.80
22.00
22.40
22.80
23.20
18
Descensos (m)
10
9
8
7
6
5
4
3
2
1
0
0,001
p1
p2
0,01
0,1
1
10
100
1000
Para P1
d = 1.65
T0= 7,6 ·10-3
Para P2
d = 1,60
T0= 6 ·10-1
10000
Tiempo (mto)
Q
360 m 3 / h 24 h / día
T1 = 0,183
= 0.183
= 960 m 2 / día
∆d10
1,65m
2,25Tt 0 2,25 ⋅ 960 m 2 / dia ⋅ 7,610 −3
S1 =
=
= 1,1 ⋅10 − 4
2
r
100 ⋅1440 min/ día
T2 = 990 m 2 / día
S 2 = 0,9 ⋅10 −4
ACUÍFERO LIBRE. METODO DE THEIS
Si los descensos no son grandes en relación
con el espesor saturado del acuífero (15%) y si
el drenaje es instantáneo y proporcional al
descenso producido, son aplicables las mismas
formulas de los acuíferos cautivos.
Se pueden corregir los descensos aplicando la
corrección de Dupuit
Hay que tener presente que los valores de S
oscilan entre 0.1 y 0.3
19
EJERCICIO
Calcular los descensos de un pozo de 0.60 m de diámetro a 10 y 100 metros
del mismo a 1 hora y 1 día de iniciado el bombeo sabiendo que el caudal
constante de bombeo es de 100 m3/hora, la transmisividad del acuífero es de
1000 m2/día y el coeficiente de almacenamiento es de 0,2. Utilizar el método
de Theis y de Jacob.
d=
100 m 3 / h 24 h
W (u ) = 0.191W (u )
4π 1000 m 2 / día
u=
2
r 2S
r 2 0, 2
−5 r
=
=
5
⋅
10
t
4Tt 4 1000 m 2 / día t
Estando r en m y t en días
Datos obtenidos a partir de las tablas de W(u) (función del pozo)
r (m)
t
u
W(u)
S(m) libre
Theis
S(m) libre
Jacob
S(m) cautivo
Theis
Pozo
0.3
1 hora
1día
1.1.10-4
4.5.10-6
8.54
11.73
1.56
2.15
1.63
2.24
3.09
3.70
10
1 hora
1día
0.12
0.005
1.66
4.73
0.30
0.87
0.29
0.90
1.74
2.35
100
1 hora
1día
12
0.05
0.00
0.56
0.00
0.09
0.00
0.02
0.80
1.47
1000
1 hora
1día
1220
50
0.00
0.00
0.00
0.00
0.00
0.00
0.086
0.600
20
Descensos
METODOS DE RECUPERACIÓN. RÉGIMEN VARIABLE
Bombeo
Parada
t
t’
B
dM
A
rva
Cu
b
de
b
om
C
eo
Cu
rva
O
t
de
i
D Curva
resid
ual
ny E
ec
c ió
n
F
tg
Tiempo
tg – t = t’
ANÁLISIS DE CAPTACIONES
• Ecuación general de descensos del pozo
• Curva característica del pozo
•Caudal de explotación
•Calidad de acabado de un sondeo
21
Caudal, Qb
Curva característica teórica de un pozo
2
1
C
3
Qbc
1. Acuífero libre
2. Acuífero confinado
3. Confinado que pasa a
libre, a partir de sp1
B
A
sp1
Descenso, sp
B
Punto crítico
Qbc Caudal óptimo de explotación
Pérdidas de carga y ecuación general de descensos
Descenso teórico = el que predicen los modelos basados en la ley de Darcy
Descenso real = mayor que el teórico, debido a las “pérdidas de carga”
Las pérdidas de carga se producen fundamentalmente:
En el pozo:
1. Debido al rozamiento del agua al atravesar el macizo de gravas
2. Por el rozamiento del agua al pasar por las ranuras de los filtros o tubería de
revestimiento; además, se produce un estrechamiento de las líneas de flujo radial y la
velocidad aumenta
3. En el interior del pozo se producen pérdidas de carga por:
• circulación del agua hasta la aspiración de la bomba, y
• las ocasionadas en la propia aspiración por no disponer de suficiente espacio
anular libre (espacio no superior a 7,62 cm)
En el acuífero:
• Las que se producen en las inmediaciones del pozo por aumento de la velocidad de
entrada al sondeo. En las proximidades del sondeo aumenta el gradiente hidráulico y,
por consiguiente, la velocidad. Si se supera el régimen laminar (no se cumple la ley de
Darcy), se provoca un “sobredescenso” proporcional a una cierta potencia del caudal
• Las que se producen en las zonas alejadas del pozo, donde la velocidad es lenta, el
régimen es laminar y se cumple la ley de Darcy.
22
carg
Pérdidas de
a
AQ + BQn
BQn
l
ta
to
o
o
ns
r ic
ce
eó
t
s
De
so
en
c
s
De
AQ
Descenso, m
Variación del descenso en función del caudal
Caudal, m3/h
Ecuación general de descensos (fórmula de Rorabaugh)
d = AQ + BQn
d
descenso total
AQ descenso teórico
BQn pérdidas de carga
d = AQ + BQn
d
descenso total
AQ descenso teórico
BQn pérdidas de carga
A se obtiene de la fórmula de Jacob
A = 0,183
1 2,25Tt
lg 2
T
r S
B = coeficiente de pérdidas de carga en el pozo y en su entorno, que no depende
del tiempo de bombeo
n = 1- 3.5 (Jacob considera n = 2)
23
Descensos
MÉTODO DE LOS BOMBEOS ESCALONADOS
d1 = AQ1 + BQ1n
Tres ensayos de bombeo
d2 = AQ2 + BQ2n
con diferentes caudales y
n
de la misma duración
d3 = AQ3 + BQ3
Escalones con recuperación
Tiempo
Nivel estático
Q1
d1
d2
Q2
Recuperación total
d3
Q3
Descensos
Tiempo
Nivel estático
d1
Q1
Q2
Recuperación parcial
d2
Q3
d3
Tiempo
Tiempo
Nivel estático
Nivel estático
∆d1
Q1
Q2
t
t
∆d2
Descensos
Descensos
Escalones sin recuperación
Q1
∆d1
∆d2
Q2
Q3
∆d3
t
Régimen permanente
(con estabilización de niveles)
t
t
Q3
∆d3
t
Régimen no permanente
(sin estabilización de niveles)
24
Resolución analítica
d1 = AQ1 + BQ1n
d2 = AQ2 + BQ2n
d3 = AQ3 + BQ3n
d 2 d1
−
Q2 Q1 Q2n −1 − Q1n −1
=
d 3 d 2 Q3n −1 − Q2n −1
−
Q3 Q2
Tanteando diferentes valores de n se puede hallar el que cumple mejor la
ecuación. Una vez determinado n, el cálculo de A y B, es elemental.
Método gráfico de tanteo de n
d1/Q1 = A +
d2/Q2 = A +
d3/Q3 = A +
Si n = 2
A, ordenada en el origen
B, pendiente de la recta
Si n ≠2, se dará a n un valor cualquiera (entre1 y
3,5) y se representarán los puntos (d/Q, Qn-1). Si se
ajusta a una recta, el valor de n es el real
BQ1n-1
BQ2n-1
BQ3n
1,0
d/Q 10-3, días/m2
0,9
n=2
0,8
0,7
0,11 10-3
0,6
1000
0,5
0,4
0,3
B = (0,11 10-3 / 1000) = 1,1 10-7 días2/m5
A = 0,35 10-3 días/m2
0,2
500
1000 1500 2000 2500 3000 3500 4000 5000
Qn-1, m3/día
25
Eficiencia de un pozo
Eficiencia =
st
AQ
=
s p AQ + BQ n
Factores
Incrustaciones y corrosión de la entubación
Depósito de arena en el interior del pozo
Penetratividad
Estudio de caudal de explotación.
Consideraciones
Diseñar ensayos para que de este ensayo pueda deducirse, con el menor
error, el caudal de explotación
Conocidos los valores de T, S, B y fijado el tiempo de duración del bombeo,
así como el descenso a producir, es fácil deducir el caudal para estas
condiciones a partir de la ecuación general.
Para fijar el descenso, es necesario analizar la situación del acuífero
(acuífero multicapa, acuífero libre, acuífero cautivo, espesor) y factores
económicos.
Para fijar el tiempo, se aconseja, a efectos de cálculo, emplear cien días.
Conocer el caudal y la altura de elevación permiten proyectar con acierto
equipos de elevación y de servicios adecuados.
El caudal depende tanto de las características del acuífero como del grado
de eficacia de la obra de captación.
Otros puntos a tener en cuenta son:
•
•
•
•
•
Proximidad al mar
Existencia de pozos que exploten el mismo acuífero
Los recursos y reservas de agua (acuíferos pequeños)
Existencia de campos de pozos (afecciones mutuas)
Estudio del descenso residual (acuíferos compartimentados y sin recursos
suficientes, régimen de bombeo cíclico)
26
Anomalías y casos particulares
Efecto de la falta de desarrollo. Las curvas sufren una serie de altibajos que
al cabo de un tiempo, en el que el pozo se desarrolla, siguen su evolución
normal.
Recargas exteriores y reciclado. Las recargas ajenas al sistema se dividen
en recargas extendidas a lo largo de una gran superficie (infiltración) y
recargas localizadas (reciclaje del agua bombeada).
Barreras impermeables (bordes negativos). Si se tiene un pozo bombeando
a una determinada distancia de un borde impermeable, los descensos
producidos serán la suma de los debidos al pozos de bombeo real más los
debidos a otro pozo imaginario (pozo imagen), situado simétricamente del
de bombeo respecto a la barrera y que hubiera comenzado a bombear al
mismo tiempo.
Recargas laterales (bordes positivos). Un borde de recarga es un sistema
superficial en el que existe agua a nivel constante y con capacidad de
recargar el acuífero (lagos, ríos, mar). SE puede aplicar el método de las
imágenes, sin más que sustituir la simulación de bombeo por una inyección
en el mismo, con el mismo caudal e iniciada al mismo tiempo.
Efectos de almacenamiento en pozos de gran diámetro
27