CÓNICAS 1 a) Clasificar la siguiente cónica según los valores del

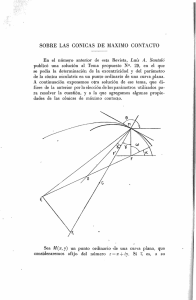
CÓNICAS
a) Clasificar la siguiente cónica según los valores del parámetro “a”:
(a 2  4)x 2  9y 2  6axy  4(a 2  1)x  12ay  4a 2  8  0 .
b) Hacer un estudio completo de la cónica anterior para a = 1:
Ecuación reducida y área de la cónica.
Semiejes, excentricidad y parámetro de la cónica.
Centro, ejes, focos y vértices principales.
Ecuaciones de las rectas que pasan por el punto (0,2) y son tangentes a la
cónica.
Dibujo de la cónica.
Unidad Docente de Matemáticas de la E.T.S.I.T.G.C. de la U.P.M.
1
CÓNICAS
c) Clasificar la siguiente cónica según los valores del parámetro “a”:
(a 2  4)x 2  9y 2  6axy  4(a 2  1)x  12ay  4a 2  8  0 .
d) Hacer un estudio completo de la cónica anterior para a = 1:
Ecuación reducida y área de la cónica.
Semiejes, excentricidad y parámetro de la cónica.
Centro, ejes, focos y vértices principales.
Ecuaciones de las rectas que pasan por el punto (0,2) y son tangentes a la
cónica.
Dibujo de la cónica.
Solución
a) Clasificación
 4a 2  8  2(a 2  1)  6a 


A 00  36  0
A    2(a 2  1)
a2  4
3a  ,

 A  324  0


3a
9 
  6a
a11  a22  A      0  ELIPSE REAL

Elipse
b) Sea a=1
Ecuación reducida
1x' '2  2 y ' '2    0
  7  13
5 3 
   1
1 y  2 valores propios de A c  
, ya que se toma como 1 el
 2  7  13
3 9 
valor propio de menor valor absoluto. k 
A
 9
A 00
(7  13)x '' 2  (7  13)y '' 2  9  0 
x '' 2
y '' 2

1
9
9
7  13 7  13
Semiejes
a2 
9
7  13
Área de la cónica
 a
S  ab 
3
7  13
, b2 
9
7  13
 b
3
7  13
3

2
Excentricidad y parámetro de la cónica
c2  a 2  b2 
a2 
9
7  13
1
c
13  e  
2
a
, b2 
9
7  13
7 13  13
18
p
b 2 2 26  5 2
.

6
a
Unidad Docente de Matemáticas de la E.T.S.I.T.G.C. de la U.P.M.
2
CÓNICAS
Centro
4  5x  3y  0
1 1
 C  , .

2 2
6  3x  9y  0
Ejes

 1 1
Pasa por el centro C  , 
Eje focal x’’  
 2 2

Es paralelo a los vectores propios asociados a  1  7  13

1
3 
1
 x   0    13  2
, 1  y   
x 
     ef  
2
2
2  13 
 y 0
 3

 A c  1I  

 1 1
Pasa por el centro C  , 
El eje no focal y’’  
 2 2
Es perpendicular al eje focal

por tanto, y’’  y 
1
3
1


x   .
2
2
2  13 
Vértices principales
Se hallan como la intersección del eje focal con la circunferencia de centro el origen y
radio “a”:
  26  3 338  78 13 26  1690  26 13 

1
3 
1
V1 

,
x  
y  2 


52
52

2
2  13 
 




2
2
9
  26  338  78 13 26  1690  26 13 
 x  1    y  1  





,
V2 
2 
2  7  13



52
52

 
Focos
Se hallan los puntos de intersección del eje focal con la circunferencia de centro el
origen y radio c:
c2  a 2  b 2 
13
2
 1
1
1

3 
F1  
x  
y  2 
  2
2
2  13 



2
2
 1
 x  1    y  1   13




F2  

2 
2
2
2
 
13  2 1
, 
4
2
13  2 


4

13  2 1
, 
4
2
13  2 


4

Haz de rectas que pasan por el punto (0,2) es y  2  mx .
Unidad Docente de Matemáticas de la E.T.S.I.T.G.C. de la U.P.M.
3
CÓNICAS
La intersección de la recta tangente con la elipse debe ser un único punto, por tanto, el
sistema
y  2  mx
5x 2  9y 2  6xy  8x  12y  4  0
2
2
2
debe
tener
(24m  4)  32(9m  6m  5)  0 ⇒ 144(2m  1)  0 ⇒ m  
solución
1
2
⇒
única
y  2
⇒
y  2
1
2
1
x
2x
Dibujo
Unidad Docente de Matemáticas de la E.T.S.I.T.G.C. de la U.P.M.
4