Cálculo de circuito con resistencias en SERIE Observa el siguiente

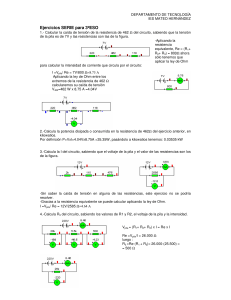
Cálculo de circuito con resistencias en SERIE
Observa el siguiente circuito, en donde los valores de las resistencias parciales son:
r1= 23 Ω; r2= 47 Ω; r3=26 Ω
1. Sabiendo que Rt = r1+r2+r3, determina la resistencia total del conjunto.
Rt = r1+r2+r3; Rt = 23+47+26 = 96 Ω, la resistencia total es de 96 Ω (ohmios)
2. Sabiendo que por la ley de Ohm la I = V/R y que la intensidad del conjunto es
siempre la misma en un circuito en donde todos los receptores están conectados en
serie, determinamos la intensidad que recorre el circuito.
I= Vt/Rt= 48/96 = 0.5 A, la intensidad total es de 0.5 Amperios
3. Sabiendo que la suma de las tensiones parciales es igual a la tensión aplicada o
tensión total, que las tensiones parciales están determinadas por las fórmulas siguientes,
calcularemos el valor de todas ellas comprobando que su suma es igual a la tensión
aplicada.
Vt = V1 +V2 +V3; V1 = It. r1; V2 = It. r2; V3 = It. r3
- V1 = It. r1; V1 = 0,5.23 = 11,5 V
- V2 = It. r2; V2 = 0,5.47 = 23,5 V
- V3 = It. r3; V3 = 0,5.26 = 13 V
- La suma de las tensiones parciales debe ser igual a la tensión total
Vt = V1 +V2 +V3 = 11,5 V + 23,5 V +13 V = 48 V
Cálculo de circuito con resistencias en PARALELO
Observa el siguiente circuito, en donde los valores de las resistencias parciales son:
r1= 5 Ω; r2= 30 Ω; r3= 10 Ω
Vt= 12 V
1. Sabiendo que determinar el valor de la resistencia total.
2. Sabiendo que por la ley de Ohm la I= V/R y que la tensión del conjunto es siempre la
misma en un circuito en donde todos los receptores están conectados en paralelo,
determinamos la intensidad total que recorre el circuito, dado que conocemos la tensión
aplicada y la resistencia total.
I= Vt/Rt; I = 12/3 = 4 A, la intensidad total es de 4 Amperios
3. Sabiendo que la intensidad total en un circuito en paralelo es igual a al suma de las
intensidades parciales y que sus valores están determinados por:
It= (Vt/r1) + (Vt/r2) + (Vt/r3) determinaremos las intensidades parciales .
I1= Vt/r1; I1 = 12/5 = 2,4 A
I2= Vt/r2; I2 = 12/30 = 0,4 A
I3= Vt/r3; I3 = 12/10 = 1,2 A
It= I1 + I2 + I3 = 2,4 + 0,4 + 1,2 = 4 A, la suma de las intensidades parciales es igual
a la total.
Aplicación del concepto de potencia eléctrica
En una bombilla ordinaria puede leerse la inscripción 60 W-220 V. Con estos datos se
trata de determinar: a) la intensidad de corriente que pasa por la bombilla cuando está
conectada a la red. b) El valor en Ω de su resistencia eléctrica. c) La energía eléctrica
expresada en joules y en kW-h que consume al cabo de dos horas de estar encendida.
La potencia eléctrica P consumida en una resistencia puede expresarse bien en la forma
P = I.V siendo I la intensidad de corriente , V la caída de potencial entre sus extremos,
bien en la forma P = I². R que combina la anterior ecuación con la ley de Ohm V = I.R.
a) El valor de la intensidad se obtiene a partir de la primera ecuación sustituyendo los
datos que aparecen grabados en la bombilla:
P = I.V
i = P/V = 60 W/220 V = 0,27 A
b) El valor de la resistencia puede calcularse, bien utilizando la segunda expresión de la
potencia, bien a partir de la ley de Ohm:
V = i.R
R = V/i = V²/P = (220 V)²/60 W = 807Ω
c) El valor de la energía eléctrica consumida en joules resulta de aplicar la noción de
potencia como energía por unidad de tiempo:
P = We/t ; We = P.t
Dado que cada hora consta de 3 600 segundos, resulta:
We = 60.2.3600 = 4,32.105.J
Recordando que 1 W = 10-3 kW, el resultado en kW-h vendrá dado por:
We = 60.10-3.kW.2.h = 0,12.