Pauta de respuesta del práctico 3.
Anuncio
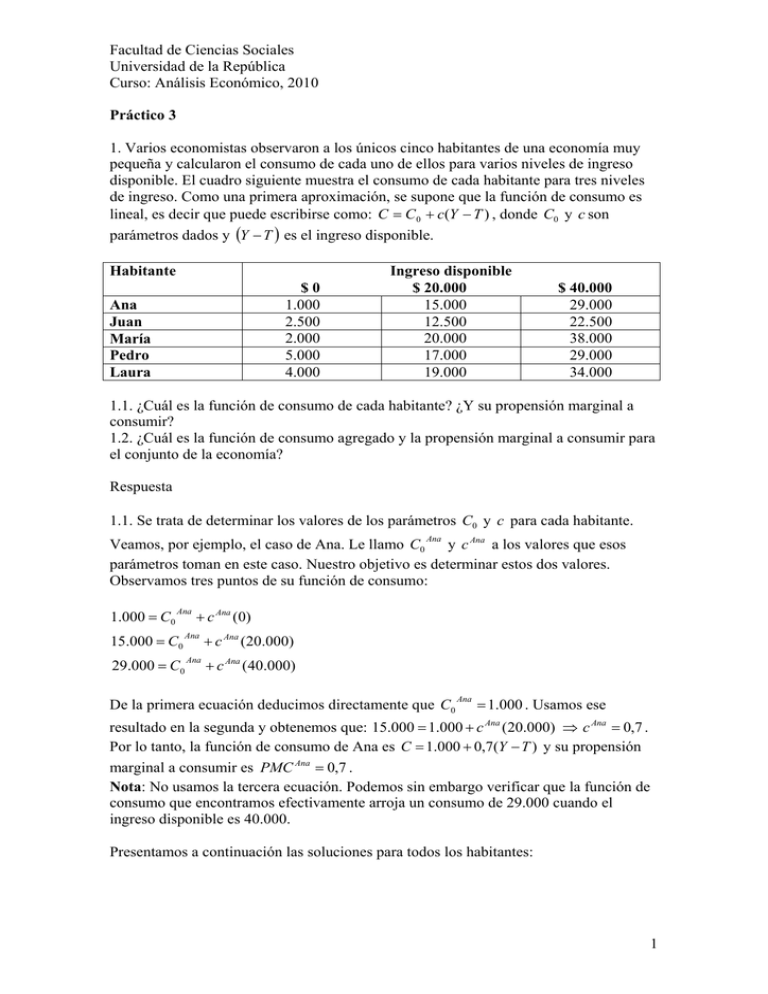
Facultad de Ciencias Sociales Universidad de la República Curso: Análisis Económico, 2010 Práctico 3 1. Varios economistas observaron a los únicos cinco habitantes de una economía muy pequeña y calcularon el consumo de cada uno de ellos para varios niveles de ingreso disponible. El cuadro siguiente muestra el consumo de cada habitante para tres niveles de ingreso. Como una primera aproximación, se supone que la función de consumo es lineal, es decir que puede escribirse como: C = C 0 + c(Y − T ) , donde C0 y c son parámetros dados y (Y − T ) es el ingreso disponible. Habitante $0 1.000 2.500 2.000 5.000 4.000 Ana Juan María Pedro Laura Ingreso disponible $ 20.000 15.000 12.500 20.000 17.000 19.000 $ 40.000 29.000 22.500 38.000 29.000 34.000 1.1. ¿Cuál es la función de consumo de cada habitante? ¿Y su propensión marginal a consumir? 1.2. ¿Cuál es la función de consumo agregado y la propensión marginal a consumir para el conjunto de la economía? Respuesta 1.1. Se trata de determinar los valores de los parámetros C0 y c para cada habitante. Ana Veamos, por ejemplo, el caso de Ana. Le llamo C0 y c Ana a los valores que esos parámetros toman en este caso. Nuestro objetivo es determinar estos dos valores. Observamos tres puntos de su función de consumo: 1.000 = C0 Ana 15.000 = C0 + c Ana (0) Ana 29.000 = C0 Ana + c Ana (20.000) + c Ana (40.000) De la primera ecuación deducimos directamente que C0 Ana = 1.000 . Usamos ese resultado en la segunda y obtenemos que: 15.000 = 1.000 + c Ana (20.000) ⇒ c Ana = 0,7 . Por lo tanto, la función de consumo de Ana es C = 1.000 + 0,7(Y − T ) y su propensión marginal a consumir es PMC Ana = 0,7 . Nota: No usamos la tercera ecuación. Podemos sin embargo verificar que la función de consumo que encontramos efectivamente arroja un consumo de 29.000 cuando el ingreso disponible es 40.000. Presentamos a continuación las soluciones para todos los habitantes: 1 Facultad de Ciencias Sociales Universidad de la República Curso: Análisis Económico, 2010 Habitante C0 1.000 2.500 2.000 5.000 4.000 Ana Juan María Pedro Laura c 0,70 0,50 0,90 0,60 0,75 1.2. Obtenemos el consumo y el ingreso agregados sumando los consumos e ingresos individuales: Consumo total $0 14.500 Ingreso disponible $ 100.000 83.500 $ 200.000 152.500 La función de consumo agregada satisface entonces las siguientes ecuaciones: 14.500 = C0 + c(0) 83.500 = C0 + c(100.000) 152.500 = C0 + c(200.000) De la primera ecuación se deduce que C0 = 14.500 . Usando este resultado en la segunda ecuación obtenemos: c = 0,69 . Es decir que la propensión marginal a consumir para el conjunto de la economía es PMC = 0,69 . 2. Entre 2000 y 2005, Eastlandia experimentó importantes fluctuaciones tanto del consumo como del ingreso disponible, aunque la riqueza, el tipo de interés y el ingreso disponible esperado no variaron. En el cuadro siguiente se puede ver el nivel de consumo e ingreso disponible agregados en millones de euros para cada uno de esos años. A partir de esa información, resuelva las siguientes preguntas: 2.1. Dibuje la función de consumo agregado de Eastlandia. 2.2. ¿Cuál es la función de consumo agregada? 2.3. ¿Cuál es la propensión marginal a consumir? ¿Y la propensión marginal al ahorro? Año 2000 2001 2002 2003 2004 2005 Ingreso disponible 100 350 300 400 375 500 Consumo 180 380 340 420 400 500 2 Facultad de Ciencias Sociales Universidad de la República Curso: Análisis Económico, 2010 Respuesta: 2.1. 600 Consumo 500 400 300 200 100 0 100 150 200 250 300 350 400 450 500 Ingreso disponible 2.2. La figura sugiere que la función de consumo de Eastlandia es lineal, es decir que puede escribirse como: C = C 0 + c(Y − T ) . Para determinar los valores de los coeficientes, usamos dos puntos cualesquiera. Elijo los dos primeros: 180 = C0 + c(100) 380 = C0 + c(350) Para eliminar C0 , resto la primera ecuación de la segunda: 380 − 180 = c(350 − 100) . Por lo tanto, la propensión marginal a consumir es: c = 0,80 . Usando este resultado en la primera ecuación, obtenemos: C0 = 100 . Por lo tanto, la función de consumo es: C = 100 + 0,80(Y − T ) . Nota: se puede verificar que los datos de ingreso disponible y consumo obtenidos en los restantes años satisfacen la función de consumo que encontramos. 2.3. La propensión marginal a consumir es PMC = 0,8 . La propensión marginal al ahorro es PMA = 1 − PMC = 1 − 0,8 = 0,2 . 3. Explique la influencia que tendrá cada una de las siguientes acciones en el nivel de inversión planeada y de inversión no planeada. Suponga que la economía se encuentra inicialmente en un equilibrio de ingreso y gasto. 3.1. El Banco Central aumenta la tasa de interés. 3.2. Se registra un aumento de la tasa de crecimiento esperada del PBI real. 3.3. Una entrada considerable de capitales procedentes del extranjero provoca un descenso de la tasa de interés en el país. Respuesta. 3.1. El aumento de la tasa de interés reduce la inversión planeada. Cae por lo tanto la demanda efectiva. Si el aumento de la tasa de interés no fue anticipado, aumenta la inversión no planeada en inventarios, ya que las empresas habrán previsto un nivel de demanda agregada mayor al que finalmente se concretó. 3 Facultad de Ciencias Sociales Universidad de la República Curso: Análisis Económico, 2010 3.2. Un aumento de la tasa de crecimiento esperada del PBI real estimula la inversión ya que se requerirá más capital en el futuro. Aumenta entonces la inversión planeada. Es lo que se conoce como el efecto acelerador del aumento del producto. No se ve afectada la inversión no planeada. 3.3. La reducción de la tasa de interés induce mayor inversión, ya que se reduce el costo del financiamiento para la inversión y se reduce el costo de oportunidad de hacer inversiones reales. Aumenta entonces la inversión planeada. No se ve afectada la inversión no planeada. 4. En el cuadro siguiente se muestra el PBI, el ingreso disponible (YD) , el consumo (C ) y la inversión planeada (I planeada ) de una economía en millones de dólares. Suponga que no existe acción alguna del Estado ni del sector externo. PBI 0 400 800 1.200 1.600 2.000 2.400 2.800 3.200 YD C 0 400 800 1.200 1.600 2.000 2.400 2.800 3.200 I planeada 100 400 700 1.000 1.300 1.600 1.900 2.200 2.500 GAplaneada I No planeada 300 300 300 300 300 300 300 300 300 4.1. Complete el cuadro, calculando el gasto planeado agregado (GAplaneado ) y la ( ) inversión no planeada en existencias I No planeada . 4.2. ¿Cuál es la función de consumo agregado? 4.3. ¿Cuál es el PBI de equilibrio ingreso-gasto, Y * ? 4.4. ¿Qué valor tiene el multiplicador? 4.5. Si la inversión planeada aumenta en 200 millones de dólares, ¿cuál será el nuevo Y *? Respuesta 4.1. PBI 0 400 800 1.200 1.600 2.000 2.400 2.800 3.200 YD 0 400 800 1.200 1.600 2.000 2.400 2.800 3.200 C I planeada 100 400 700 1.000 1.300 1.600 1.900 2.200 2.500 300 300 300 300 300 300 300 300 300 GAplaneada I No planeada 400 700 1.000 1.300 1.600 1.900 2.200 2.500 2.800 - 400 - 300 - 200 - 100 0 100 200 300 400 4 Facultad de Ciencias Sociales Universidad de la República Curso: Análisis Económico, 2010 4.2. Suponemos nuevamente que la función de consumo es lineal, es decir que puede escribirse como C = C 0 + c(Y − T ) . Sabemos entonces que: 100 = C0 + c(0) 400 = C0 + c(400) De la primera ecuación deducimos que: C0 = 100 y usando este resultado en la segunda ecuación obtenemos: c = 0,75 . Si la función fuera efectivamente lineal, la recta que encontramos debería pasar por todos los otros puntos que se presentan en el cuadro. Verifico que pasa por el punto YD = 3.200; C = 2.500 : C0 + c(3.200) = 100 + 0,75(3.200 ) = 2.500 . 4.3. El PBI de equilibrio se obtiene cuando la inversión no planeada es cero. En este caso es PBI = 1.600 . 4.4. El multiplicador es m = 1 =4 1 − 0,75 4.5. Una forma de responder es rehacer el cuadro. Otra forma es utilizar la función de consumo que acabamos de estimar. Seguimos este segundo procedimiento. Sabemos que: Y =C+I C = C0 + cY Notar que, con los supuestos realizados, YD = Y . 1 (C0 + I ) 1− c La inversión planeada es ahora 500 y, por lo tanto: Y = 4(100 + 500 ) = 2.400 Sustituimos: Y = C0 + cY + I ⇒ Y = El producto de equilibrio pasó de 1.600 a 2.400, es decir que aumentó en 800. Este aumento del producto resulta de un aumento de la inversión planeada de 200 y un multiplicador de 4. 5. En una economía sin acción alguna del Estado ni sector externo, el consumo autónomo es 250 millones de dólares, la inversión planeada es 350 millones de dólares y la propensión marginal a consumir es 2 3 . 5.1. Dibuje la función de consumo agregado y la recta del gasto agregado planeado. 5.2. ¿Cuál es el PBI de equilibrio ingreso-gasto, Y * ? 5.3. ¿Cuál es la inversión no planeada en existencias si el PBI real es 600 millones de dólares? 5.4. ¿Qué valor tiene el multiplicador? 5.5. Si la inversión planeada aumenta a 450 millones de dólares, ¿cuál será el nuevo Y *? 5 Facultad de Ciencias Sociales Universidad de la República Curso: Análisis Económico, 2010 Respuesta 5.1. Sabemos que C = C0 + cY = 250 + (2 3)Y C, GAp GAp C 600 450 250 300 Y 5.2. El equilibrio se produce cuando se verifican las siguientes dos ecuaciones: Y =C+I C = 250 + (2 3)Y Por lo tanto, el ingreso de equilibrio es: Y = 250 + (2 3)Y + 350 ⇒ Y * = 1.800 5.3. El gasto planeado cuando el PBI = 600 es: GA = 250 + (2 3)600 + 350 = 1.000 . Tenemos entonces que el producto es 400 millones menos que el gasto planeado. La inversión no planeada en existencias será entonces igual a - 400 millones (suponiendo que existe ese monto de inventarios). 5.4. Con una propensión marginal a consumir de 2/3, el multiplicador resulta 1 m= =3 1− 2 3 5.5. Si la inversión planeada aumenta a 450 millones, el ingreso de equilibrio pasa a ser: Y = 250 + (2 3)Y + 450 ⇒ Y * = 2.100 6. Una economía tiene una propensión marginal al consumo de 0,5 y el PBI de equilibrio ingreso-gasto, Y * , es 500 millones de dólares. Complete el cuadro siguiente y muestre la secuencia de incremento del consumo que se daría si la inversión planeada se incrementara en 10 millones de dólares. Las dos primeras filas ya están hechas. En la primera fila, el incremento de la inversión planeada de 10 millones de dólares provoca un aumento de la misma magnitud en el PBI real, haciendo que se eleve a su vez el consumo en 5 millones de dólares en la segunda fila. 6 Facultad de Ciencias Sociales Universidad de la República Curso: Análisis Económico, 2010 Secuencia 1 2 3 4 5 6 7 8 9 10 ΔI planeada 10 0 0 0 0 0 0 0 0 0 ΔC 0 5 ΔY 10 5 6.1. ¿Cuál es la variación total en el PBI real tras las diez secuencias? ¿Cuál es el valor del multiplicador? ¿Cuál esperaría que fuera la variación total de Y* aplicando la fórmula del multiplicador? 6.2. Vuelva a completar el cuadro suponiendo esta vez que la propensión marginal al consumo es 0,75. ¿Cuál es la variación total del PBI real tras las diez secuencias? ¿Cuál es el valor del multiplicador? Al aumentar la propensión marginal a consumir, ¿qué le sucede al valor del multiplicador? Respuesta 6. Secuencia 1 2 3 4 5 6 7 8 9 10 ΔI planeada 10 0 0 0 0 0 0 0 0 0 ΔC 0,00 5,00 2,50 1,25 0,63 0,31 0,16 0,08 0,04 0,02 ΔY 10,00 5,00 2,50 1,25 0,63 0,31 0,16 0,08 0,04 0,02 6.1. El aumento acumulado de PBI en las diez secuencias es 19,99 millones de dólares. El multiplicador en este caso es 2. La variación total del producto debería ser 1 ΔY * = 10 = 20 . Es decir que al haber transcurrido diez secuencias, se ha 1 − 0,5 producido ya la mayor parte del aumento esperado total del producto. 7 Facultad de Ciencias Sociales Universidad de la República Curso: Análisis Económico, 2010 6.2. Con PMC = 0,75 tenemos: Secuencia 1 2 3 4 5 6 7 8 9 10 ΔI planeada 10 0 0 0 0 0 0 0 0 0 ΔC 0,00 7,50 5,63 4,22 3,16 2,37 1,78 1,33 1,00 0,75 ΔY 10,00 7,50 5,63 4,22 3,16 2,37 1,78 1,33 1,00 0,75 La variación del PBI después de las diez secuencias es 37,75 millones de dólares. El multiplicador es ahora 4. Aumentó debido al aumento de la propensión marginal a consumir. 8


