AYUDANTÍA N°6 • • •

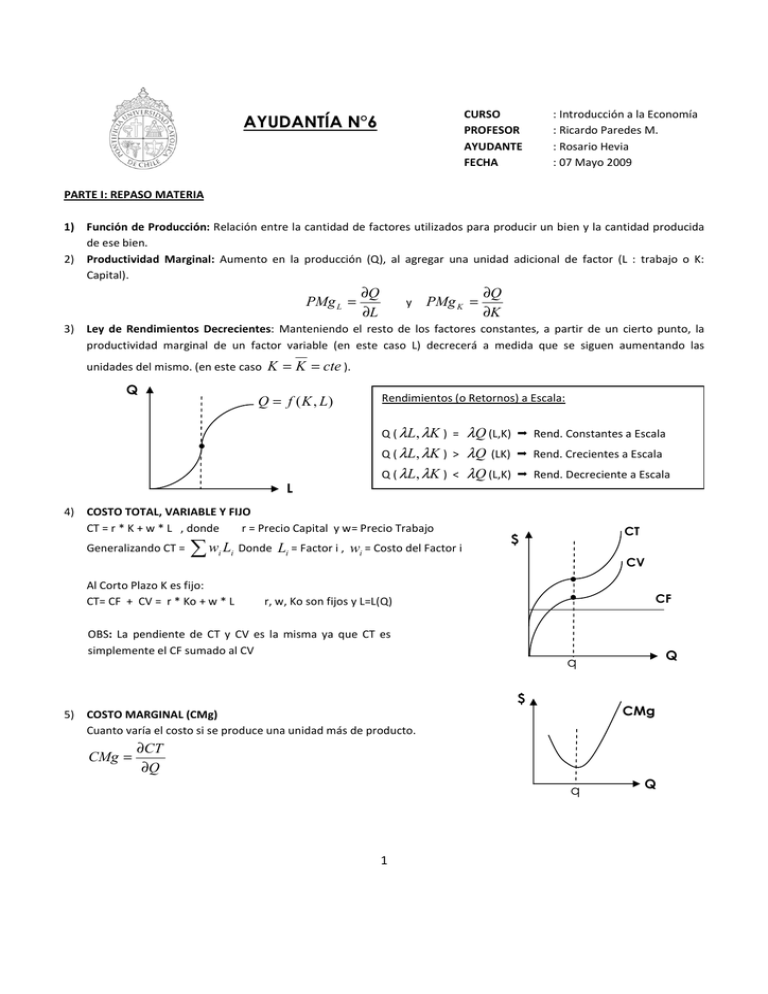
CURSO
PROFESOR
AYUDANTE
FECHA
AYUDANTÍA N°6
: Introducción a la Economía
: Ricardo Paredes M.
: Rosario Hevia
: 07 Mayo 2009
PARTE I: REPASO MATERIA
1) Función de Producción: Relación entre la cantidad de factores utilizados para producir un bien y la cantidad producida
de ese bien.
2) Productividad Marginal: Aumento en la producción (Q), al agregar una unidad adicional de factor (L : trabajo o K:
Capital).
PMg L =
∂Q
∂L
y
PMg K =
∂Q
∂K
3) Ley de Rendimientos Decrecientes: Manteniendo el resto de los factores constantes, a partir de un cierto punto, la
productividad marginal de un factor variable (en este caso L) decrecerá a medida que se siguen aumentando las
unidades del mismo. (en este caso
Q
K = K = cte ).
Q = f ( K , L)
Rendimientos (o Retornos) a Escala:
Q ( λ L , λK ) =
•
Q ( λ L , λK ) >
Q ( λ L , λK ) <
λQ (L,K)
λQ (LK)
λQ (L,K)
Rend. Constantes a Escala
Rend. Crecientes a Escala
Rend. Decreciente a Escala
L
4) COSTO TOTAL, VARIABLE Y FIJO
CT = r * K + w * L , donde
r = Precio Capital y w= Precio Trabajo
Generalizando CT =
∑ wi Li Donde Li = Factor i , wi = Costo del Factor i
CT
$
CV
Al Corto Plazo K es fijo:
CT= CF + CV = r * Ko + w * L
•
•
r, w, Ko son fijos y L=L(Q)
CF
OBS: La pendiente de CT y CV es la misma ya que CT es
simplemente el CF sumado al CV
Q
q
$
CMg
5) COSTO MARGINAL (CMg)
Cuanto varía el costo si se produce una unidad más de producto.
CMg =
∂CT
∂Q
q
1
Q
6) COSTO MEDIO (CTMe, CVMe, CFMe)
CTMe = CT/Q
CVMe = CV/Q
CFMe = CF/Q siempre decrece
CMg > CMe CMe aumenta con Q
CMg < CMe CMe disminuye con Q
7) OFERTA DE LA EMPRESA
La curva de CMg de la empresa es la Oferta de la Empresa Competitiva:
- Al Corto Plazo: Desde 1 en adelante (Bajo 1, cerrar la empresa)
- Al Largo Plazo: Desde 2 en adelante (Bajo 2, salir del mercado)
8) ANALIZANDO LOS PRECIOS y BENEFICIO
$
Se produce en CMg = P
CMg
CTMe
Po
CVMe
BENEFICIO ()
π = Ingreso – Costos
π = Po*Qo – CTMe*Qo
π = Qo ( Po – CTMe)
•2
•
1
El beneficio esta representado por el área:
CFMe
Q
9) MERCADO PERFECTAMENTE COMPETITIVO:
a) Muchos Compradores y vendedores tales que ninguno puede influir en el precio de mercado.
b) Productos homogéneos (idénticos)
c) Libre entrada y salida de empresas
d) Información perfecta (los compradores saben todos los precios y compran al más barato)
10) OFERTA DE LA INDUSTRIA:
a) n fijo
2
b) Libre entrada y salida de empresas
A cualquier Precio P > Po, las firmas tienen ganancias, por lo
que más firmas ingresan al mercado, el precio cae y dejan de
haber ganancias.
Si aumenta la demanda de D a D’, hay ganancias y por lo tanto
entran (Q2 – Q1)/Qo firmas extras a la industria.
BENEFICIO (π)
π = Ingresos – Costos
π = Po*Qo – CTMe*Qo = Qo ( Po – CTMe)
Luego, vemos que:
π = 0 Si P=CTMe
π>0
Si P>CTMe (entran firmas)
π<0
Si P<CTMe (salen formas)
11) MONOPOLIO
En monopolio se produce menos que en competencia perfecta provocando una perdida social
Empresa Competitiva:
En un Monopolio:
P = IMg = CMg
P > IMg = CMg
P
CTMe
Pm
= Beneficios
del Monopolista
CMg
El Beneficio será:
π = Ingresos – Costos
π = Pm*Qm – CTMe*Qm
π = Qm (Pm – CTMe)
D
IMg
Q
Qm
3
PARTE II: EJERCICIOS RESUELTOS
1) Comente:
a) En un Mercado Competitivo una empresa puede sostener ganancias positivas para siempre.
FALSO. En un mercado competitivo no existen barreras de entrada, por lo que si una empresa tiene ganancias
positivas, otras empresas entraran a la industria, por lo cual bajaran sus precios y se repartirán estas ganancias,
llegando al punto en que una empresa tendrá ganancias nulas.
b) El equilibrio de un mercado competitivo P=CMg no implica que una empresa gane dinero en el corto plazo
Verdadero, el supuesto de P=CMg siempre se cumple tanto en el largo como el corto plazo, una empresa puede ser
sustentable en el futuro aunque tenga perdidas en el corto plazo. Esto ocurre cuando una empresa llega cubrir sus
costos variables, pero tiene ingresos menores a los costos totales.
c)
Explique las diferencias entre Rendimientos a Escala y Ley de Rendimientos Decrecientes.
Rendimientos (o Retornos) a Escala: Se refieren a cuanto varía la producción cuando varían todos los factores.
Pueden ser Retornos Constantes, Creciente o Decrecientes a Escala.
Ley de Rendimientos Decrecientes: Se refiere a como varía la Productividad Marginal de un factor variable y se deja
todo el resto de los factores constante.
d) Cómo serán los rendimientos de la siguiente función de producción como por ejemplo f(K,L,M)= ln(KLM)
Productividades Marginales:
F ( K , L, M )=Ln( KLM )
F (αK , αL, αM )=Ln(αKαLαM ) = Ln(α 3 KLM ) = 3Ln(α ) + Ln( KLM )
Por lo tanto tenemos que:
Si 3Ln (α ) + Ln ( KLM ) = αLn ( KLM ) Tendremos rendimientos constantes a escala.
Si 3Ln (α ) + Ln ( KLM ) < αLn ( KLM ) Tendremos rendimientos decrecientes a escala.
Si 3Ln(α ) + Ln( KLM ) > αLn( KLM ) Tendremos rendimientos crecientes a escala.
e) Comenta la siguiente afirmación: “el equilibrio de un mercado competitivo P=CMg no implica que una empresa
gane dinero en el corto plazo”.
VERDADERO. El supuesto de P=CMg siempre se cumple, tanto en el largo como el corto plazo. Pero una empresa
puede ser sustentable en el futuro aunque tenga perdidas en el corto plazo. Esto ocurre cuando una empresa llega
cubrir sus costos variables, pero tiene ingresos menores a los costos totales.
f)
“Las empresas en equilibrio competitivo producen solo en la medida que tienen beneficios”.
FALSO. En equilibrio competitivo los beneficios de las empresas son nulos, ya que CMe=CMg.
2) Para una cierta industria: los costos marginales en el corto plazo de cada empresa son: CMg=4q y en la que si la
empresa por cualquier motivo no produce nada igual tiene que pagar un arriendo de $250. Calcule la función de
costos totales y costos medios de cada empresa.
Como
De esta forma:
4
Pero en el enunciado me dicen que los costos fijos son iguales a $250, luego:
3
2
2
3) Suponga una firma con la siguiente función de costos totales: CT(Q)=0,04Q -0,9Q +(11-k)Q +5k Esta firma se enfrenta
a un precio P=$4 (mercado perfectamente competitivo):
a) Encuentre la cantidad producida por la firma en el corto plazo. Asuma k=4.
Tengo P =
Entonces,
CMg en el equilibrio, CMg = 0,12Q 2 − 1,8Q + 7
4 = 0,12Q 2 − 1,8Q + 7
Q1 = 1,9 , Q2 = 13
Hay que ver cual de estas dos soluciones da el máximo beneficio a la empresa. Para esto, vemos la segunda derivada
de la función de beneficios:
δ 2 Π δ 2 CT
δCMg
=
=−
= 1,8 − 0,24Q
2
2
δQ
δQ
δQ
Π = PQ − CT
Para encontrarnos en un máximo, la segunda derivada debe ser menor que cero Q=13.
Calculamos los beneficios:
Π = 4 ⋅ 13 − 0,04 ⋅ 133 + 0,9 ⋅ 132 − 7 ⋅ 13 − 80 = −54,78
Tiene pérdidas. Como estamos viendo el corto plazo, debemos ver cuales son los costos medios variables para Q=13.
Si son menores que $4, la empresa seguirá produciendo.
CV = 0,04Q 3 − 0,9Q 2 + 7Q
Por lo tanto sigue produciendo. Producirá
13 unidades, que venderá a $4,
obteniendo pérdidas de $54,78.
2
CVMe = 0,04Q − 0,9Q + 7
CVMe(13) = 0,04 ⋅ 13 2 − 0,9 ⋅ 13 + 7 = 2,06
b) Encuentre cuanto produce la firma en el largo plazo.
En el largo plazo se pueden modificar los factores fijos para poder minimizar los costos, k es variable.
3
2
Min CT(Q)=0,04Q -0,9Q +(11-k)Q +5k
2
δCT
= −Q + 10k = 0
δk
3
2
k=
Q
10
2
Entonces los costos totales quedan: CT(Q)=0,04Q -0,9Q +(11-Q/10)Q +5(Q/10)
Igualando precio a costos marginales:
4 = 0,12Q 2 − 1,8Q + 11 −
Q1 = 5,13
Q Q
+
5 10
Q2 = 10
Revisamos cual maximiza beneficios:
δ 2Π
δCMg
=−
= 2,1 − 0,24Q
2
δQ
δQ
Por lo tanto producirá Q=10. Calculamos beneficios:
Π = 4 ⋅ 10 − 0,04 ⋅ 103 + 0,9 ⋅ 102 − 10 ⋅ 10 − 5 = −15
Por lo tanto, como estamos en una situación de largo plazo y hay pérdidas, la empresa cierra.
5
c) Compare los anteriores resultados. ¿Por qué son distintos o iguales?
En el caso del corto plazo, la empresa no puede cambiar sus costos fijos, por lo que si puede vender algo a un precio
mayor que sus costos variables, es mejor que nada, por que de todas formas deberá pagar la mano de obra, o
arriendo, insumos, etc. Pero en el largo plazo la empresa puede gestionar sus costos fijos, comprando menos/más
insumos, contratando más empleados, buscando otro local donde ubicarse.
4) Mencione y grafique los tres casos que ocurren en un mercado competitivo a corto plazo.
Los tres casos son:
1. Precio está por bajo los costos variables
2. El precio está entre los costos totales y los costos variables.
3. El Precio está sobre sobre los costos totales.
1
2
3
Analizando cada caso:
a) Cuando el precio está bajo los Costos Variables, a la empresa le conviene cerrar para disminuir sus pérdidas. Ya
que sus ganancias no alcanzan a cubrir sus CV, ni sus CF, por lo cual sigue generando pérdidas.
b) Cuando el precio está entre los Costos Totales y los Costos Variables, aunque el productor percibe pérdidas, no
cierra y se mantiene en el mercado, esto debido a que con sus ganancias, aunque no cubre todos los CT, cubre
los CV y parte del CF (por lo tanto puede ir amortizando su CF y perder menos que la situación en que decide
cerrar)
c) Cuando el precio está sobre los Costos Totales, el productor percibe utilidades netas equivalentes al rectángulo
amarillo, y costos equivalentes al rectángulo en rojo.
5) Considere una industria que enfrenta en conjunto una demanda que se puede representar por P = 100.000- Q. Cada
empresa en la industria tiene la siguiente función de costos totales: CT = 20 + 30q - 4q2 + 0,2q3
a) Determine la oferta de esta empresa y la oferta de la industria si inicialmente hay 100 empresas iguales, tanto
para el corto como para el largo plazo (recuerde, siempre con 100 empresas).
Oferta empresa corto plazo: CMg de la empresa desde intersección con costo medio variable.
Oferta industria corto plazo: CMg de la industria desde intersección con costo medio variable.
En este caso, los costos totales son todos variables, por lo que no hay cambios en el largo plazo.
En el Largo Plazo:
CMg=CMe 30 − 8q + 0,6q 2 = 20 / q + 30 − 4q + 0,2 ⋅ q 2
6
Resolviendo: q=10,46 y CMe(10,46)=11,95
En el Corto Plazo:
CMg=CVMe 30 − 8q + 0,6q 2 = 30 − 4q + 0,2 ⋅ q 2
Resolviendo: q=10 y CVMe(10)=10
Luego, la oferta de la empresa será:
LP:
CP:
P > 11,95
P > 10
y
y
P = 30 − 8q + 0,6q 2
q > 10,46
q > 10
Y la oferta industria:
Como hay 100 empresas: (100q=Q )
2
 Q 
 Q 
2
CMg = 30 − 8
 + 0,6
 = 30 − 0,08 ⋅ Q + 0,006 ⋅ Q
 100 
 100 
Por lo tanto, la oferta de la industria será:
LP:
CP:
P > 11,95
P > 10
y
y
P = 9,5 − 0,2 ⋅ Q + 0,015Q 2
q > 1046
q > 1000
b) Suponga ahora que hay libre entrada y salida de empresas. Determine la oferta de la Industria.
Si hay libre entrada y salida de empresas, los beneficios totales van a ser nulos ya que las empresas producen a sus
CMe mínimos (nivel en que CMe=CMg). Esto se calcula en el LP, ya que al CP la industria no alcanza a reaccionar.
Como se explicaba anteriormente, si todas las empresas tienen la misma estructura de costos, cada empresa va a
producir en el mínimo de su costo medio, y va a cobrar ese costo medio, es decir la Oferta será: P = 11,95.
c)
¿Cuánto producirá la empresa con Precios $10 y $11? Explique si hay alguna diferencia.
Ambos precios están por sobre los CMeV, por lo tanto al CP produce con ambos precios:
P = 10 q = 10
y
P = 11 q = 10,21
A su vez, ambos precios están bajo los CMeT por lo tanto al LP no produce a ninguno de los dos precios.
d) Suponga que la industria se monopoliza. Determine cuánto se produce, a que precio, y la Pérdida Social Compare
el precio al que produce el monopolista.
Demanda: P = 100.000 - Q
IMg = 100.000 – 2Q
7
Para calcular la cantidad producida por el monopolio tenemos que IMg = P:
100.000 – 2Q = 11,95 Q = 49994,025, Reemplazando en la Demanda P = 50005,075
Luego, la Pérdida Social será: PS
=
1
(Dda(49994) − IMg (49994)) * (Qmonopolio − Qcomp. perfecta )
2
1
PS = (50006 − 12 ) * (49994 − 988,05) = 122.367.857
2
2
3
6) Considere una empresa típica en una industria competitiva, que tiene una función de CT(q) = 100q – 10q + q .
Suponga además que la industria se puede representar por P =1000 – Q.
a) Si hay libre entrada y salida de empresas, determine: el precio de competencia perfecta, la producción y el
número de empresas.
En competencia perfecta, con libre entrada y salida de empresas, el beneficio de éstas es cero, por lo cual cada una
produce cuando: CMg = CMe
Como
CMg =
dCT (q )
CT
= 100 − 20q + 3q 2 y CMg =
= 100 − 10q + q 2
dq
q
Al igualar nos quedan 2 soluciones: q=0 (que se descarta) y q=5 (que es la que usamos)
Luego, cada empresa produce 5 unidades.
El precio de venta será el CMg evaluado en la cantidad que se produce: CMg(5)=75
Por lo tanto el precio de venta es $75
Veamos la cantidad demandada a un precio de $75, es decir: 75 = 1000 – Q, luego, la cantidad demanda es 925
unidades.
Finalmente vemos el número de empresas. Si cada firma produce 5, y la cantidad demanda es 925, con libre entrada
y salida de empresas habrá n = Q/q = 925/5 firmas, es decir, 185 empresas.
b) Si el número de empresas esta fijo en 100. Determine la oferta, el precio y las utilidades de cada empresa.
Si ahora se fija el numero de empresas, se debe buscar la nueva curva de oferta, luego tenemos que q=Q/100 por lo
tanto la nueva curva de oferta será:
O:
P = CMg (q=Q/100) = 100 – 0,2Q – 0,0003Q2
Ahora es necesario encontrar el precio de mercado, para lo cual: OFERTA = DEMANDA
100 – 0,2Q – 0,0003Q2 = 1000 – Q y resolviendo tenemos que:
Q = 852,48
P = 147,52
c)
Suponga ahora que la industria se monopoliza, es decir pasa enteramente a las manos de un operador y se
prohíbe la entrada de otros. Determine el precio, cantidad producida por cada planta del monopolista (lo que
antes era una firma, ahora es una planta), la producción total de la industria y la pérdida social.
8
Cuando existe solo una empresa en el mercado, estamos hablando de monopolio, y en este caso, el monopolista,
para maximizar sus beneficios, produce cuando CMg = IMg.
Analizamos para cada fábrica:
CMg =
dCT (q )
= 100 − 20q + 3q 2
dq
Para el I = P*q = (1000 – Q)*q= (1000 – 100q)*q = 1000q-100q
IMg =
2
dI
= 1000 − 200q
dq
Igualando CMg = IMg tenemos que:
q = 4,65
: Lo que produce cada fábrica del monopolista
Q = 100*q = 465 : Lo que produce el monopolista en total
P = 1000-Q = 535
OBSERVACION: Para simplificar el desarrollo del ejercicio, asumimos que cada planta produce q=4,65. Sin embargo,
estrictamente esto no ocurre, sino que cada planta produce q=5 unidades. Pero como al monopolista le conviene
producir Q=465 unidades para maximizar su beneficio, en total tendría
n = 465/5 = 93 plantas, cada una
produciendo 5.
9