Método de Runge-Kutta-Fehlberg aplicado a la ecuación

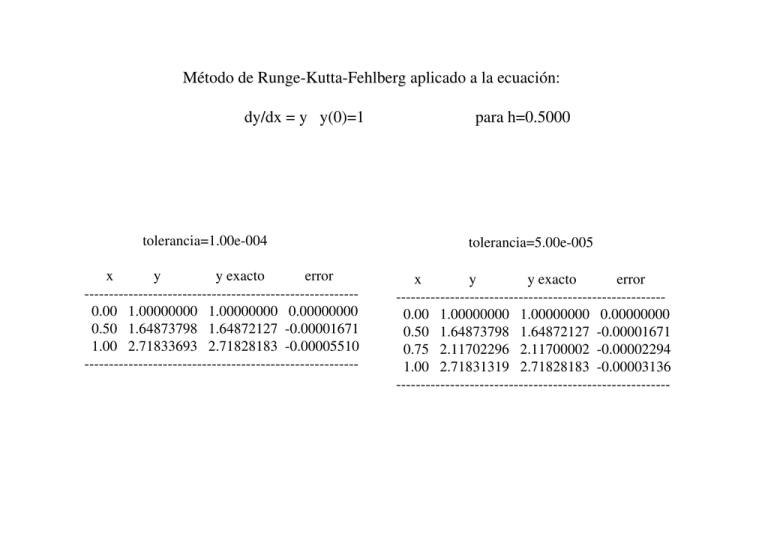
Método de Runge-Kutta-Fehlberg aplicado a la ecuación:
dy/dx = y y(0)=1
tolerancia=1.00e-004
x
y
y exacto
error
-------------------------------------------------------0.00 1.00000000 1.00000000 0.00000000
0.50 1.64873798 1.64872127 -0.00001671
1.00 2.71833693 2.71828183 -0.00005510
--------------------------------------------------------
para h=0.5000
tolerancia=5.00e-005
x
y
y exacto
error
------------------------------------------------------0.00 1.00000000 1.00000000 0.00000000
0.50 1.64873798 1.64872127 -0.00001671
0.75 2.11702296 2.11700002 -0.00002294
1.00 2.71831319 2.71828183 -0.00003136
--------------------------------------------------------
Método de Runge-Kutta-Fehlberg aplicado a la ecuación:
dy/dx = -y y(0)=1
tolerancia=1.00e-004
x
y
y exacto
error
------------------------------------------------------0.00 1.00000000 1.00000000 0.00000000
0.50 0.60647035 0.60653066 0.00006031
1.00 0.36780629 0.36787944 0.00007315
-------------------------------------------------------
para h=0.5000
tolerancia=5.00e-005
x
y
y exacto
error
------------------------------------------------------0.00 1.00000000 1.00000000 0.00000000
0.50 0.60647035 0.60653066 0.00006031
0.75 0.47231863 0.47236655 0.00004793
1.00 0.36784137 0.36787944 0.00003807
--------------------------------------------------------
Método de Runge-Kutta-Fehlberg aplicado a la ecuación:
dy/dx = (x-y)/2 y(0)=1
tolerancia=1.00e-005
x
y
y exacto
error
------------------------------------------------------0.00 1.00000000 1.00000000 0.00000000
0.50 0.83639761 0.83640235 0.00000474
1.00 0.81958460 0.81959198 0.00000738
-------------------------------------------------------
para h=0.5000
tolerancia=5.00e-006
x
y
y exacto
error
-------------------------------------------------------0.00 1.00000000 1.00000000 0.00000000
0.50 0.83639761 0.83640235 0.00000474
0.75 0.81186355 0.81186784 0.00000428
1.00 0.81958811 0.81959198 0.00000387
--------------------------------------------------------