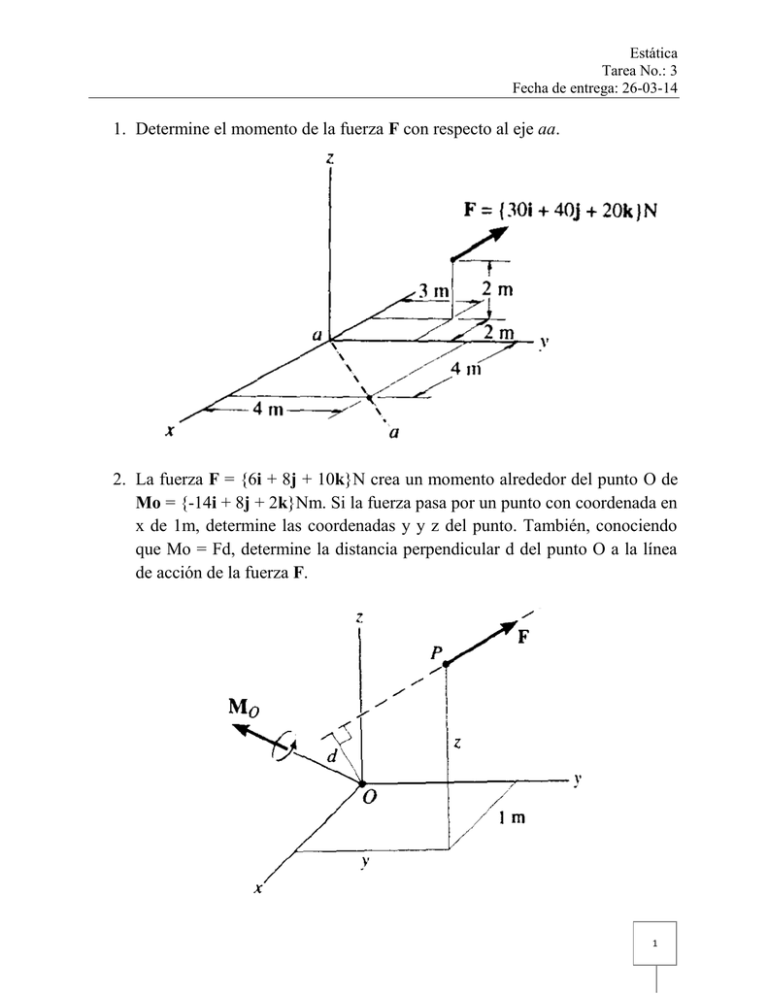
1. Determine el momento de la fuerza F con respecto al eje aa. 2. La

Estática
Tarea No.: 3
Fecha de entrega: 26-03-14
1. Determine el momento de la fuerza F con respecto al eje aa.
2. La fuerza F = {6i + 8j + 10k}N crea un momento alrededor del punto O de
Mo = {-14i + 8j + 2k}Nm. Si la fuerza pasa por un punto con coordenada en
x de 1m, determine las coordenadas y y z del punto. También, conociendo
que Mo = Fd, determine la distancia perpendicular d del punto O a la línea
de acción de la fuerza F.
1
Estática
Tarea No.: 3
Fecha de entrega: 26-03-14
3. Los sistemas de fuerzas coplanares, A y B mostrados, son equivalentes.
Sabiendo que F1 es igual a -20i N, F2 es -10j N, las magnitudes de F4 y F5
son 8 N y el momento de R con respecto al origen es -220k N·m, determine
F3 y R, así como un punto del soporte de F1.
4. Considere los puntos A(1,-3,1), B(-2,1,1), C(0,2,0), D(0,0,-1) y E(3,0,0)
cuyas coordenadas están dadas en metros, así como una fuerza F de
magnitud igual a 10 N, cuyo soporte pasa por A y por B, y tiene sentido
dirigido de B hacia A. Con base en ello:
a) Obtenga el vector representativo de F.
b) Determine los momentos de F respecto a cada uno de los ejes coordenados,
haciendo intervenir a los puntos C, D y E, según proceda.
c) Compruebe que la suma de esos tres momentos que se pidió determinar en el
inciso anterior, es igual al momento de F respecto al origen.
2
Estática
Tarea No.: 3
Fecha de entrega: 26-03-14
5. Dado el par de fuerzas, cada una de magnitud 8 kN, que se muestra en la
siguiente figura, determine:
a) el momento de dicho par,
b) geométicamente, la distancia más corta entre las líneas de acción de las
fuerzas que constituyen el par, y,
c) empleando la distancia obtenida en el inciso b), corrobore el resultado pedido
en el inciso a).
3