Document

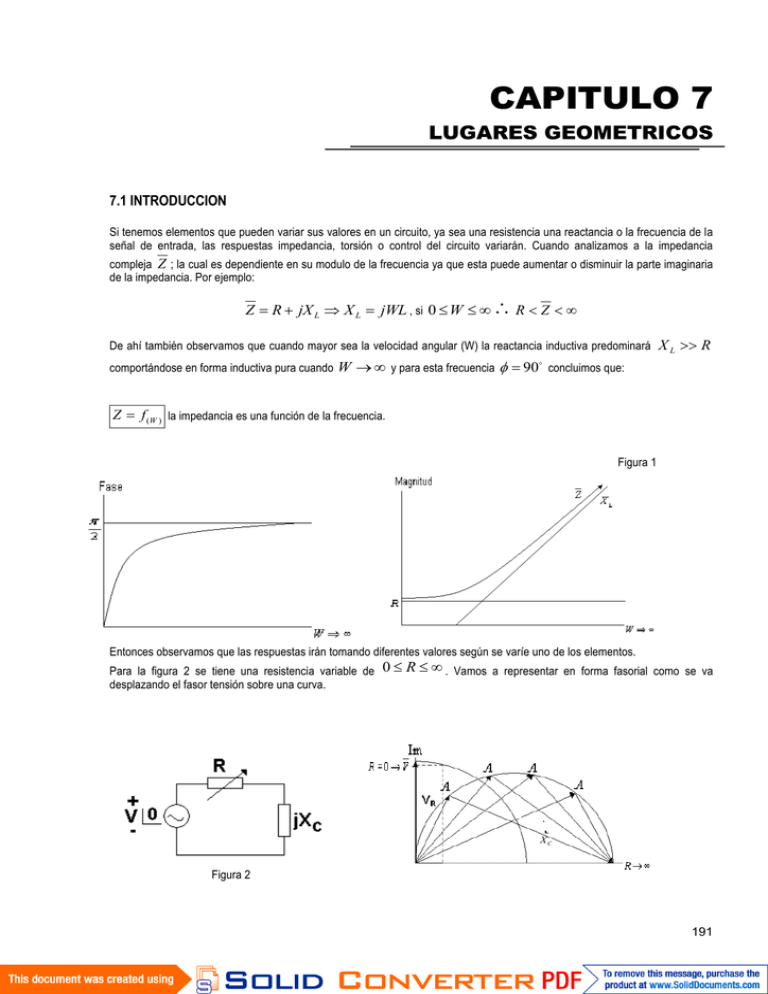
CAPITULO 7
LUGARES GEOMETRICOS
7.1 INTRODUCCION
Si tenemos elementos que pueden variar sus valores en un circuito, ya sea una resistencia una reactancia o la frecuencia de la
señal de entrada, las respuestas impedancia, torsión o control del circuito variarán. Cuando analizamos a la impedancia
compleja Z ; la cual es dependiente en su modulo de la frecuencia ya que esta puede aumentar o disminuir la parte imaginaria
de la impedancia. Por ejemplo:
Z  R  jX L  X L  jWL , si 0  W    R  Z  
De ahí también observamos que cuando mayor sea la velocidad angular (W) la reactancia inductiva predominará
comportándose en forma inductiva pura cuando
X L  R
W   y para esta frecuencia   90 concluimos que:

Z  f (W ) la impedancia es una función de la frecuencia.
Figura 1
Entonces observamos que las respuestas irán tomando diferentes valores según se varíe uno de los elementos.
Para la figura 2 se tiene una resistencia variable de
desplazando el fasor tensión sobre una curva.
0  R   . Vamos a representar en forma fasorial como se va
XC
Figura 2
191
Podemos ver el comportamiento del circuito que al variar la resistencia desde cero hasta
esta se va incrementando y la tensión sobre
R   el valor de la tensión sobre
X C va disminuyendo, y vemos como el punto A se desplaza sobre la curva de la
semicircunferencia hasta cuándo R   que el circuito se comporta como resistivo puro cayendo toda la tensión de la fuente
sobre la resistencia variable.
7.2 LUGAR GEOMÉTRICO DE LAS IMPEDANCIAS Y ADMITANCIAS PARA R VARIABLE
a)
Para la impedancia: Z  R  jX , como la reactancia es fija, es decir tendrá un solo punto sobre el eje
imaginario, el par ordenado (R, X) que representa a la impedancia se irá desplazando sobre la recta paralela al eje de
las abscisas (real) así tendremos una idea más general del comportamiento de la impedancia cuando 0  R   y
para sus valores limites R  0  Z  jX  R   Z  R
W =constante
jX =constante
0 R
b)
Para las admitancias: debemos tener en cuenta que las escalas de la admitancia es diferente a la escala con que
hemos graficado el lugar geométrico de las impedancias.
Z  R  jX
Y

Y  G  jB
1
………. (1)
R  jX
A partir de la ecuación (1) podemos obtener los valores limites para la grafica de las admitancias
R  0Y 
1
1
j
jX
X
y cuando
R Y  0
192
Sería muy tedioso si comenzamos a trabajar punto por punto por lo que haremos las siguientes operaciones hasta encontrar
una expresión adecuada que me represente al conjunto de todos los valores de las admitancias.
*
1
Y
Z  Z 
*
Y
YY
G
B 

Z  R  jX  2
 j 2
2
2 
G B
 G B 
B
B
X  2
 G2  B2   0
2
G B
X
2
Lugar geométrico de las
impedancias
2
B  1   1 
2
B  
 
 G  0
X  2X   2X 
Lugar geométrico de las
2
admitancias
2
1 

 1 
2
B
 G  

2X 

 2X 
7.3 LUGAR GEOMÉTRICO DE LAS ADMITANCIAS E IMPEDANCIAS PARA X AJUSTABLE
Z  R  jX
Igual que el caso anterior
Cuando X
Cuando
0
0  X   , solo que ahora el elemento a variar es la reactancia de cero a infinito
Z  R resistivo
X   Z  inductivo
Aquí R permanece constante junto con la frecuencia, solo estamos variando es el valor de la inductancia o del capacitor.
El lugar geométrico de las impedancias será la línea paralela al eje de las
ordenadas (Im).
El segmento de la recta positiva representa para todas las soluciones en
que Z es inductivo y el segmento de recta negativo en el que la
impedancia se comporta capacitivamente
Para el caso de la admitancia que es la inversa de la impedancia compleja,
por lo tanto a partir de la expresión Y 
1
encontramos los valores
Z
mínimos y máximos.
Y
1
R  jX
1
R
X 0
Y
X 
Y 0
193
Para encontrar todos los puntos del lugar geométrico, trabajamos:
Z
1
G
B 

 2
 j 2
 R  jX
2
2 
Y G B
 G B 
Como R es constante
R
G
G
 G2  B2   0
2
G B
R
2
2
2
G  1   1 
2
G  
 
 B 0
R  2R   2R 
2
2
1 

 1 
2
 G 
 B 

2R 

 2R 
X 
2
X 0
Podemos observar que el lugar geométrico de las admitancias es un semicírculo de radio
1
2R
Podemos observar que el lugar geométrico para los casos analizados impedancia y admitancia hay una transformación de un
segmento de recta en el eje positivo o negativo a una semicircunferencia situada en el eje negativo y positivo respectivamente.
7.4 ADMITANCIA EN FUNCIÓN DE LA VARIACIÓN A SUS ELEMENTOS
En los siguientes gráficos se puede ver que los ejes cartesianos son G y B, en la cual podemos determinar el lugar geométrico
de la admitancia.
Hay dos casos: con resistencia variable y reactancia variable.
Con resistencia variable. En el circuito que se representa en la figura N° 3, se observa con una impedancia con resistencia
variable la cual se convierte a admitancia.
Figura N° 3.Circuito de impedancia a admitancia
194
Sabemos:
Z=
Entonces:
Z = R + JX … (α)
Y = G + JB … (β)
De (α)y (β):
G
B
R + JX = (
) − J(
)
G +B
G +B
Racionalizando e igualando las partes reales e imaginarias, tenemos:
G
… (I)
G +B
X=−
… (II)
R=
De la ecuación (II)
B
G +B =−
X
B
G +B + =0
X
Dando forma:
B
1
1
+
=
X
2X
2X
1
1
G + B+
=
2X
2X
G +B +
Bueno llegamos a una ecuación de una circunferencia de
Despejando B:
B=

Si:
1
2X
−G −
1
2X
Para una impedancia inductiva: Z⃗ = Zθ
G = 0 → B = 0 o′ B = −
G=
→B=−
195
Grafico N° 3. Admitancia con comportamiento inductivo en resistencia variable

Si:
Para una impedancia capacitiva: Z⃗ = Z−θ
G=0 →B=0 ; B=
G=
→B=
;
Grafico N° 4. Admitancia con comportamiento capacitivo en resistencia variable
196
Con Reactancia variable: En el circuito que se representa en la figura N° 4, se observa con una impedancia con reactancia
variable la cual se convierte a admitancia.
Figura N° 4.Circuito de impedancia a admitancia
Ahora trabajamos con la ecuación (I):
Dándole forma:
Entonces:
Llegamos a una ecuación de circunferencia de radio
Despejando:

Para una impedancia inductiva:
Si:
197
En el plano Y⃗:
Grafico N° 5. Admitancia con comportamiento inductivo en reactancia variable

Para una impedancia capacitiva Z⃗ = Z−θ
Si:
B=0 →G=
B=
→G=
yG= 0
Grafico N° 5. Admitancia con comportamiento capacitivo en reactancia variable
198
LUGARES GEOMETRICOS
PROBLEMAS RESUELTOS
PROBLEMA N° 01
Encontrar el lugar geométrico de las impedancias y admitancias para el circuito mostrado:
Resolución:
Podemos observar que cuando el valor de la resistencia va de cero a infinito la admitancia toma sus valores límites, siendo una
línea paralela a las abscisas su lugar geométrico, de lo estudiado anteriormente podemos decir que su lugar geométrico de las
impedancias será un semicírculo en el eje negativo
0R
Z
1
1

Y 1  jWC
R
1
Y   jWC  G  jB
R
PROBLEMA N°02
En el siguiente circuito determine usted si existe algún valor de
RL para la condición de resonancia, además trazar el lugar
geométrico de admitancia del circuito.
199
Resolución:
Para la rama R-C es una admitancia de valor fijo que podemos representarla en el plano complejo como un vector cuyo modulo
y argumento lo podemos calcular
Z1  4  5 j
Fijo
Y  0.0975  0.122 j
Y1  0.156 51.34º
Para la rama R-L como R varia su lugar geométrico de las admitancias será un semicírculo de radio 0.05 y este se calcula
cuando R = 0
Y1
Y2
0.122
Lugar geométrico de las admitancias
jB
0.05
1
R  j10
 1 
Es una semicircunferencia de radio 

 2X 
1
  j 0.05
20
Z 2  R  j10 Variable Y2 
0.05
YT  Y1  Y2
YT
51.34º
0.0975
0.022
G
Como no hay cruce con el eje real no hay resonancia
¿Qué es la resonancia?
Se denomina resonancia de un circuito serie o paralelo cuando la reactancia de la impedancia total se anula es decir que el
circuito se comporta resistivo puro.
Z  R  jX  R  jX  0
Esto se da para una determinada frecuencia o cuando se varia uno de los elementos del circuito. Es decir, el circuito esta en
fase y se dice que tiene un factor de potencia unitario.
PROBLEMA N° 03
Del circuito de la figura se pide:
Dibujar el diagrama de impedancias a los terminales A-B del
circuito.
Para que condiciones el circuito tiene un factor de potencia
unitaria.
200
Resolución:
La impedancia 1 tiene un valor fijo y la podemos representar en el plano en el eje positivo superior, en cambio la impedancia 2,
su lugar geométrico es un semicírculo de radio
RC
2
Z total  Z 1  Z 2
Z 1  R  jX L
Z2
1
Y2 
 jWC
RC
Para
las condiciones para que el circuito
sea resonante usted debe analizar del
gráfico y sacar sus conclusiones
PROBLEMA N° 04
Trazar el lugar geométrico de la intensidad de corriente que circula por el circuito mostrado y hallar el valor de RC para el que
diferencia de fase entre V e I sea 45⁰.
Resolución:
La admitancia de la rama fija es de 1/R=0.1. El diámetro de la semicircunferencia del lugar geométrico de la rama RC será en
Rc=0 es decir D=1/|XC| y el radio:
El grafico será:
201
Diagramas del lugar geométrico
Se observa que la intensidad esta adelantada respecto a la tensión un ángulo de 45⁰ en le
que los putos real e imaginario de Yt deben ser iguales:
punto indicado esto significa
De:
De donde: RC=2Ω
PROBLEMA N° 05
El circuito de la fig. Debe resonar a 455KHz. Para este caso el valor de X, impedancia del circuito, el factor de calidad y además
tiene un lugar geométrico de la admitancia con escala adecuada.
Resolución:
202