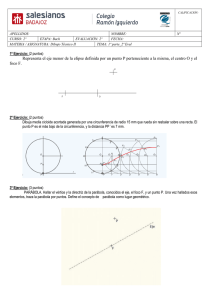
Parábola Propiedades geométricas

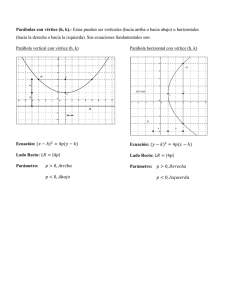
MATEMATICAS GRADO DECIMO
SEGUNDO PERIODO
TEMAS
•
Parábola
•
Elipse
•
Hipérbola
Parábola
Es una sección cónica generada al cortar un cono recto con un plano paralelo a la
directriz.
Se define también como el lugar geométrico de los puntos que equidistan de una recta
(eje o directriz) y un punto fijo llamado foco.
La parábola aparece en muchas ramas de las ciencias aplicadas, debido a que las
gráficas de ecuaciones cuadráticas son parábolas. Por ejemplo, la trayectoria ideal del
movimiento de los cuerpos bajo la influencia de la gravedad.
Propiedades geométricas
Diferentes elementos de una parábola.
Aunque la definición original de la parábola es la relativa a la sección de un cono recto
por un plano paralelo a su directriz, actualmente es más común definir la parábola como
un lugar geométrico:
Una parábola es el lugar geométrico de los puntos equidistantes
de una recta dada, llamada directriz, y un punto fijo que se
denomina foco.
De esta forma, una vez fija una recta y un punto se puede construir una parábola que los
tenga por foco y directriz de acuerdo a la siguiente construcción. Sea T un punto
cualquiera de la recta directriz. Se une con el foco dado F y a continuación se traza la
mediatriz (o perpendicular por el punto medio) del segmento TF. La intersección de la
mediatriz con la perpendicular por T a la directriz da como resultado un punto P que
pertenece a la parábola. Repitiendo el proceso para diferentes puntos T se puede
aproximar tantos puntos de la parábola como sea necesario.
De la construcción anterior se puede probar que la parábola es simétrica respecto a la
línea perpendicular a la directriz y que pasa por el foco. Al punto de intersección de la
parábola con tal línea (conocida como eje de la parábola) se le conoce como vértice de
la parábola y es el punto cuya distancia a la directriz es mínima. La distancia entre el
vértice y el foco se conoce como Distancia focal o Radio focal.
Los puntos de la parábola están a la
misma distancia del foco F y de la recta
directriz.
Construcción de puntos en una parábola.
Lado recto
El lado recto mide 4 veces la distancia focal
Al segmento de recta comprendido por la parábola, que pasa por el foco y es paralelo a
la directriz, se le conoce como lado recto.
La longitud del lado recto es siempre 4 veces la distancia focal.
Siendo D, E los extremos del lado recto y T, U las respectivas proyecciones sobre la
directriz, denotando por W la proyección del foco F sobre la directriz, se observa que
FEUW y DFWT son cuadrados, y sus lados miden FW=2FV. Por tanto el segmento DE
es igual a 4 veces el segmento FV (la distancia focal).
Las tangentes a la parábola que pasan por los extremos del lado recto forman ángulos de
45° con el mismo, consecuencia de que FEUW y DFWT sean cuadrados, junto con la
construcción mencionada en la sección anterior. Además, tales tangentes se cortan en la
directriz, precisamente en el punto de proyección W del foco, propiedades que pueden
ser aprovechadas para construir una aproximación geométrica del foco y la directriz
cuando éstos son desconocidos.
Semejanza de todas las parábolas
Todas las parábolas son similares, es únicamente la escala la que crea la apariencia de
que tienen formas diferentes.
Dado que la parábola es una sección cónica, también puede describirse como la única
sección cónica que tiene excentricidad e = 1. La unicidad se refiere a que todas las
parábolas son semejantes, es decir, tienen la misma forma, salvo su escala.
Desafortunadamente, al estudiar analíticamente las parábolas (basándose en
ecuaciones), se suele afirmar erróneamente que los parámetros de la ecuación cambian
la forma de la parábola, haciéndola más ancha o estrecha. La verdad es que todas las
parábolas tienen la misma forma, pero la escala (zoom) crea la ilusión de que hay
parábolas de formas diferentes.
Un argumento geométrico informal es que al ser la directriz una recta infinita, al tomar
cualquier punto y efectuar la construcción descrita arriba, se obtiene siempre la misma
curva, salvo su escala, que depende de la distancia del punto a la directriz.
Tangentes a la parábola
La tangente bisecta el ángulo entre el foco, el punto de tangencia y su proyección.
Un resultado importante en relación a las tangentes de una parábola establece:
La tangente biseca el ángulo entre el foco, el punto de tangencia y
su proyección.
En lo sucesivo, F denotará el foco de una parábola, P un punto de la misma y T su
proyección sobre la directriz. Retomando la construcción dada para encontrar puntos de
una parábola, sea MP la mediatriz del triángulo FPT, el cual es isósceles y por tanto
biseca al ángulo FPT. Lo único que hay que verificar ahora es que MP también es la
tangente en el punto P. Sea Q otro punto de la parábola y sea U su proyección en la
directriz.
Puesto que FQ=QU y QU<QT, entonces FQ<QT. Dado que esto es cierto para
cualquier otro punto de la parábola, se concluye que toda la parábola está de un mismo
lado de MP, y como la desigualdad es estricta, no hay otro punto de la parábola que
toque a la recta MP, esto quiere decir que MP es la tangente de la parábola en P.
Aplicaciones prácticas
Una consecuencia de gran importancia es que la tangente refleja los rayos paralelos al
eje de la parábola en dirección al foco. Las aplicaciones prácticas son muchas: las
antenas satelitales y radiotelescopios aprovechan el principio concentrando señales
recibidas desde un emisor lejano en un receptor colocado en la posición del foco.
La concentración de la radiación solar en un punto, mediante un reflector parabólico
tiene su aplicación en pequeñas cocinas solares y grandes centrales captadoras de
energía solar.
Análogamente, una fuente emisora situada en el foco, enviará un haz de rayos paralelos
al eje: diversas lámparas y faros tienen espejos con superficies parabólicas reflectantes
para poder enviar haces de luz paralelos emanados de una fuente en posición focal. Los
rayos convergen o divergen si el emisor se desplaza de la posición focal.
Ecuaciones de la parábola
Parábolas tipo y=ax2, con a=4, 1, 1/4 y 1/10.
Prueba geométrica de la relación y=ax2.
Con el advenimiento de la geometría analítica se inició un estudio de las formas
geométricas basado en ecuaciones y coordenadas.
Una parábola cuyo vértice está en el origen y su eje coincide con el eje de las ordenadas,
tiene una ecuación de la forma y=ax2 donde el parámetro a especifica la escala de la
parábola, incorrectamente descrita como la forma de la parábola, ya que como se dijo
antes, todas las parábolas tienen la misma forma. Cuando el parámetro es positivo, la
parábola se abre «hacia arriba» y cuando es negativo se abre «hacia abajo».
Si bien, la expresión en forma de ecuación no fue posible hasta el desarrollo de la
geometría analítica, la relación geométrica expresada en la ecuación anterior ya estaba
presente en los trabajos de Apolonio, y se bosquejará a continuación usando notación
moderna.
Tomando nuevamente la definición de parábola como sección de un cono recto de
forma paralela a la directriz, sea V un punto en el eje y sea QV perpendicular al eje. (QV
corresponde al valor x en la versión analítica y PV al valor y). Considerando la sección
circular que pasa por Q y es paralela a la base del cono, obtenemos H, K paralelos a B y
C.
Por el teorema de potencia de un punto:
.
Al ser PM paralela a AC, los triángulos HVP, HKA y BCA son semejantes y así:
.
Usando nuevamente los paralelismos:
.
Despejando HV y VK para sustituir en la fórmula de QV² resulta en
.
Pero el valor de
por lo que haciendo
es una constante pues no depende de la posición de V,
arroja la expresión moderna y=ax².
Parábolas verticales, con ecuaciones de la forma y=ax²+bx+c.
Aplicando una sustitución de coordenadas podemos obtener ahora la ecuación de una
parábola vertical para cualquier posición de su vértice.
La ecuación de una parábola cuyo eje es vertical y su vértice es
(u,v) tiene la forma (y-v)=a(x-u)2,
agrupando los términos y reordenando se obtiene una forma equivalente:
La ecuación de una parábola cuyo eje es vertical es de la forma
.
Si la parábola es horizontal, se obtienen ecuaciones similares pero intercambiando y por
x y viceversa. Así tendríamos:
La ecuación de una parábola cuyo eje es horizontal es de la forma
.
Ecuación involucrando la distancia focal
Ecuación de una parábola vertical.
Pueden haber muchas parábolas que tengan un mismo vértice (variando el parámetro a)
en la primera ecuación. Sin embargo, dados dos puntos fijos, existe sólo una parábola
que los tiene por vértice y foco ya que la directriz queda automáticamente fija como la
perpendicular a la línea que une el foco con el vértice y a esa misma distancia del
último.
Consideremos el caso especial en que el vértice es (0,0) y el foco es (0,p). La directriz
es por tanto, la recta horizontal que pasa por (0,-p). A la distancia entre el vértice y el
foco se le llama distancia focal, de modo que en este caso la distancia focal es igual a p.
Con esta configuración se tiene:
La ecuación de una parábola con vértice en (0,0) y foco en
(``p´´,0) es
.
De forma alterna:
La ecuación de una parábola con vértice en (0,0) y foco en (0,p) es
.
Es de notar que el coeficiente 4p es precisamente la longitud del lado recto de la
parábola.
Ambas ecuaciones se refieren a parábolas verticales que se abren «hacia arriba». La
ecuación de una parábola que se abre hacia abajo es similar excepto que varía un signo.
En este caso, el foco sería (0,-p) y de esta forma:
La ecuación de una parábola con vértice en (0,0) y foco en (0,-p)
es
.
Cuando la parábola es horizontal «hacia la derecha», se obtiene una ecuación similar
intercambiando los roles de x, y:
La ecuación de una parábola con vértice en (0,0) y foco en (p,0) es
,
obteniendo mediante un cambio de signo la ecuación de las parábolas hacia la izquierda.
Finalmente, las ecuaciones cuando el vértice no está en el centro se obtienen mediante
una traslación. En el caso común de la parábola vertical hacia arriba se tiene
La ecuación de una parábola con vértice en (h, k) y foco en (h,
k+p) es
,
mientras que para la parábola horizontal se intercambia x con y.
Ejercicios.
1. Usando la definición, hallar la ecuación de la parábola que tiene su foco en
F(2,0) y su dirección DD es la recta de ecuación x = -2.
Solución:
Trácese la gráfica con los elementos dados.
De acuerdo a la definición, un punto
Pero,
Luego,
Elevando ambos miembros al
cuadrado, se tiene:
fig. 6.5.1.
De donde y2 = 8x es la ecuación de la parábola
pedida.
2. Dada la parábola que tiene por ecuación
x2 = -6y, encontrar las coordenadas del foco, la ecuación de la directriz, analizar la
simetría de la curva y trazar la gráfica.
Solución:
la ecuación x2 = -6y tiene la forma de la ecuación (4) del teorema 1. Entonces, 2p
= -6, de donde p= -3 < 0.
Como p < 0, la parábola se abre
hacia abajo.
El foco se encuentra sobre el eje y
en el punto F (0, -p/2).
La ecuación de la directriz es la
recta
,
es decir,
Fig 6.5.2
3. Dado el punto del plano B(a, b) con a, b > 0. Demostrar que por el punto B pasa
la parábola
(1).
Determine el foco y la ecuación de la directriz
Solución:
Como
se sigue que el punto B(a, b) satisface la ecuación (1) y por
lo tanto B pertenece a la parábola.
Ahora, de acuerdo a la parte ii
del teorema 1.
con lo
cual
En consecuencia, el foco se
encuentra localizado
en el punto
ecuación de la directriz
y la
es la recta
fig 6.5.3
4. Dada la ecuación (y�)2 = 4x�, referida al sistema x�-y� en donde el nuevo
origen es el punto (2, 3). Hallar la ecuación de la gráfica en términos de x e y.
Solución:
La ecuación (y�)2 = 4x� representa en el sistema x�-y� una parábola con vértice
en O�(2, 3). La parábola se abre hacia la derecha y además 2p = 4, de donde
p = 2. Con lo cual
= distancia del vértice al foco.
Fig. 6.5.4.
Dado que O� (2, 3) se deduce de las relaciones (1) y (2) de la sección 6.1.2. que:
de donde
Sustituyendo los valores de x� e y� en la ecuación inicial, se obtiene:
Esta última ecuación, representa una parábola cuyo vértice es el punto V (2, 3),
abierta hacia la derecha y cuya distancia del vértice al foco y del vértice a la
directriz es 1.
5. Determine el vértice V y la ecuación de la parábola que tiene como directriz la
recta de ecuación x = 2 y cuyo foco está localizado en el punto F(4, 2).
Solución:
Como la directriz es la recta de ecuación x = 2, paralela al eje y, se sigue que el eje
focal es paralelo al eje x y como el foco es el punto F(4, 2), entonces el eje focal
tiene como ecua- ción y = 2.
El vértice V de la parábola está sobre la recta y = 2 y localizado en el punto medio
entre la directriz y el foco.
Como QF = p = 2, se sigue que QV = VF = 1, y por lo tanto las coordenadas del
vértice son V(3, 2).
fig. 6.5.5.
Ahora, la ecuación de la parábola viene dada por:
ó
6. Determine el vértice V, el foco F, la ecuación de la directriz, el eje focal y dibujar
la gráfica de la parábola cuya ecuación es:
Solución:
Se debe expresar la ecuación en la forma:
(1)
Así,
(Completación de cuadrados)
(2) (Factorizando)
Comparando (1) y (2) se deduce q ue:
Así que las
coordenadas del
vértice
son
.
Como p = 4 > 0 y la
variable lineal es y, se
deduce
entonces que la
parábola se abre hacia
arriba.
El eje focal es la recta
paralela al eje y de
ecuación
y el foco se encuentra
localizado en el punto
,
esto es,
fig. 6.5.6.
La directriz es la recta paralela al eje x, de ecuación
; esto
es,
En la figura 6.5.6. aparece la gráfica de la parábola con todos sus elementos.
7. Para la parábola
demostrar que el vértice está
en el punto
acuerdo al signo de a.
y que corresponde a un máximo o un mínimo de
Solución.
La ecuación:
forma:
, puede escribirse en la
.
Completando un cuadrado perfecto en el primer miembro de la última igualdad, se
tiene:
Con lo cual,
Al comparar esta última ecuación, con la igualdad (1) del teorema 2 (sección
6.1.3.), se deduce que el punto
son las coordenadas del
vértice de la parábola y además,
Ahora, si a > 0, entonces p > 0 y la parábola se abre hacia arriba. En este caso, el
punto V corresponde a un punto mínimo de la parábola.
Si a < 0, entonces p < 0 y la parábola se abre hacia abajo. En este caso, el punto V
corres- ponde a un punto máximo de la parábola.
8. (Propiedad óptica (o focal) de la parábola)
Demostrar que la normal a la parábola en un punto Q, hace ángulos iguales con la
recta que pasa por Q y F y con la paralela al eje focal trazada por el punto.
Solución.
Considere la parábola y2 = 2px que aparece en la figura 6.5.7., la normal nn y la
tangente
tt a la curva en el punto Q(x1, y1). Al trazar las rectas que pasan por Q y F y la
paralela al eje focal, se forman los ángulos θ y β .
fig. 6.5.7.
Se debe probar que θ =β .
La ecuación de la tangente tt a la curva en el punto Q(x1, y1) viene dada
.
por:
De aquí se deduce que
Ahora,
Asi que
Pero,
.
.
(1).
En el triángulo QFN, se tiene,
Luego,
y por lo tanto
, de donde
.
.
.
De esta forma:
(puesto que y12=2Px1)
Es decir,
Luego,
.
y por tanto θ = β.
La propiedad demostrada anteriormente, significa que si se supone un espejo
parabólico perfectamente liso, como el ángulo de incidencia es igual al ángulo de reflexión, todo
rayo para- lelo al eje de simetría de la parábola, se refleja pasando por el foco.
Esta propiedad conocida como la propiedad óptica (o focal) de la parábola es
utilizada en la construcción de reflectores y de antenas parabólicas.
.
.. Elipse
Es el lugar geométrico de los puntos del plano tales que la suma de las distancias a dos
puntos fijos llamados focos es una constante positiva e igual a la distancia entre los
vértices.
Una elipse es la curva cerrada que resulta al cortar la superficie de un cono por un plano
oblicuo al eje de simetría –con ángulo mayor que el de la generatriz respecto del eje de
revolución
Elementos de una elipse
Elementos de una elipse.
La elipse posee un «eje mayor», trazo AB, y un «eje menor», trazo CD; la mitad de cada
uno de esos ejes recibe el nombre de «semieje», de tal manera que se los denomina
«semieje mayor» y «semieje menor», respectivamente.
Sobre el «eje mayor» existen dos puntos
El punto
y
que se llaman «focos».
puede estar ubicado en cualquier lugar del perímetro de la «elipse».
Puntos de una elipse
Si F y F' son dos puntos del plano y d es una constante mayor que la distancia FF', un
punto M pertenecerá a la elipse, si:
donde es el semieje mayor de la elipse.
Excentricidad de una elipse
La excentricidad de una elipse es la razon entre su semidistancia focal y su semieje
mayor; se encuentra entre cero y uno.
•
e = c/a (0 < e < 1)
La excentricidad indica la forma de una elipse; una elipse será más redondeada cuanto
más se aproxime su excentricidad al valor cero.
Constante de la elipse
Para la elipse de la figura de la izquierda la constante es 10, dado que la longitud
medida desde el foco al punto (ubicado en cualquier lugar del perímetro de la
elipse), es la recta color azul, la que sumada a la longitud desde el foco a ese mismo
punto , es la recta color rojo. El resultado de la suma de la longitud de ambas rectas
(azul + roja), constituye para la elipse una cantidad constante, la cual siempre será igual
a la longitud del «eje mayor», trazo AB de la elipse en estudio.
La recta correspondiente, tanto trazo
(recta color azul), como al
(recta color
rojo), se las llama «radio vector». Los dos «focos» equidistan del centro .
En la animación, el punto viaja por el perímetro de la elipse.Punto al cual convergen
ambas rectas (azul y roja).
Ecuación de la elipse
La ecuación de una elipse en coordenadas cartesianas, con centro en el origen, es:
donde a > 0 y b > 0 son los semiejes de la elipse (a corresponde al eje de las abscisas, b
al eje de las ordenadas). El origen O es la mitad del segmento [FF']. La distancia entre
los focos FF' se llama distancia focal y vale 2c = 2ea, siendo e la excentricidad y a el
semieje mayor.
Si el centro de la elipse se encuentra en el punto (x', y'), la ecuación es:
En coordenadas polares una elipse viene definida por la ecuación:
La ecuación paramétrica de una elipse es:
con
, y donde el ángulo θ se puede interpretar como el ángulo polar.
Recta tangente a una elipse
La recta tangente a una elipse, con centro en (h, k), en el punto M (X1,Y1) tiene como
ecuación:
Área interior de una elipse
El área de la superficie interior de una elipse es:
Siendo a y b los semiejes.
Longitud de una elipse
El cálculo del perímetro de una elipse requiere del cálculo de integrales elípticas de
segunda especie
Sin embargo, el matemático Ramanujan entrega una formula más simple que solamente
se aproxima al valor real que tiene el perímetro de la elipse, pero con un grado no tan
satisfactorio como lo hace la integrales elípticas de segunda especie. Para su formula,
Ramanujan, entre otros valores, utiliza el “semieje mayor” y el “semieje menor”.
Fórmula para calcular el perímetro de una elipse:
Propiedades notables
La elipse goza de cierta propiedades asociadas a sus componentes, como se puede ver
en Analogía de Michelson y Morley.
La elipse como cónica
La elipse surge de la intercessión de un cono con un plano de tal manera que la
inclinación del plano no supere la inclinación de la recta generatriz del cono,
consiguiendo así una que la intersección sea una curva cerrada. En otro caso el corte
podría ser una hipérbola o una parábola, es por ello que a todas estas figuras
bidimencionales se las llaman secciones cónicas o simplente cónicas.
la elipse como conica
La elipse como hipotrocoide
La elipse es un caso particular de hipotrocoide, donde R = 2r, siendo R el radio de la
circunferencia directriz, y r el radio de la circunferencia generatriz.
En una curva hipotrocoide, la circunferencia que contiene al punto generatriz, gira
tangencialmente por el interior de la circunferencia directriz.
La elipse como caso particular de hipotrocoide. Datos: R = 10, r = 5, d = 1.
Anamorfosis de un círculo en una elipse
Esta es una circunferencia, en donde el plano cartesiano no se encuentra deformado.
Esta circunferencia por la anamorfosis queda aplastada y se transforma en una elipse, el
eje de las Y se ha contraído y el de las X se ha dilatado.
Las propiedades de la elipse como herramienta para la anamorfosis
anamorfosis de un cuadrado en un rectángulo.
La desfiguración de la circunferencia (con su aplastamiento distorsiona el plano
cartesiano asociado a ella), se denomina anamorfosis, que corresponde a una
perspectiva muy especial. El término anamorfosis se toma del griego que significa
"trasformar".
En el caso del círculo, el plano cartesiano está compuesto por varios cuadraditos, en
cambio, cuando el círculo se aplasta –transformándolo en una elipse– esos cuadrados se
deforman quedando más contraídos por el eje Y, y dilatados simultáneamente por el eje
X, según se visualiza en la imagen.
Ejemplo
Utilizando las propiedades que tiene el «semieje mayor» y, a la vez, la relación de
afinidad con la Circunferencia principal, o la Excentricidad, o la Contracción de
Lorentz, constataremos que para el ejemplo y los valores dados, podemos determinar el
factor asociado al ángulo
y, a la vez, el factor del ángulo
, tendremos:
Si el radio "Y" del círculo es de 80 m y éste se contrajo a 20 m, dado que (80 - 60), y el
radio "X" de 80 m se dilató en 140 m, dado que (80 + 60), entonces en la elipse su
«semieje mayor» será de 100 m, y su «semieje menor» de 60 m, por cuanto los valores
alteradores son 80 y 60, por lo que el
El trazo
será de 20 m, y el trazo
, será de 80.
•
Si dividimos 20/80 = 0,25 igual al factor de contracción del eje de las Y, en
donde 80 x 0, 25 = 20 = (80- 60)
•
Si dividimos 140/80 = 1,75 igual al factor de dilatación del eje de las X, en
donde 80 x 1,75 = 140 = (80 + 60)
Dado que
•
Los valores involucrados en este ejemplo son:
La elipse en mecánica celeste
En mecánica celeste, un cuerpo sometido a la atracción gravitatoria de otro y que gira a
su alrededor, describe una órbita elíptica ideal. Uno de los focos de la elipse coincide
con el cuerpo atractor. La excentricidad de la trayectoria depende de las condiciones
iniciales. Esto está descrito en las leyes de Kepler.
Ejercicios
1. Halle la ecuación de la elipse que tiene su centro en (0, 0) y cuyos focos son los
puntos
F(3, 0) y F�(-3, 0), además el intercepto de la gráfica con el eje x es el punto (5,
0).
Solución:
Como la elipse corta al eje x en el punto (5, 0) se sigue que a = 5 y como c = 3
(fig. 6.5.8) se tiene que,
y por tanto
.
fig. 6.5.8.
De esta forma, los vértices de la elipse son los puntos V1(5, 0), V2(-5, 0), V3(0, 4) y
V4(0, -4). Además, su ecuación viene dada por :
2. Trazar la elipse cuya ecuación viene dada por:
25x2 + 4y2 = 100
Solución:
La ecuación: 25x2 + 4y2 = 100, puede escribirse en las formas equivalentes:
x
4
2
+ y 2= 1 (porqué?)
25
La última ecuación corresponde a una elipse centrada en el origen cuyo eje mayor
es b = 5 y eje menor es a = 2. Además, los focos de la elipse están localizados
sobre el eje y.
De otro lado,
, de donde
se encuentran localizados en los puntos
y en consecuencia, los focos
y
.
Además, los vértices de la elipse son los puntos: V1(2, 0), V2(5, 0), V3(-2, 0) y V4(5, 0).
La figura 6.5.9. recoge toda la información obtenida.
fig. 6.5.9.
3. Determine el centro, los vértices, los focos y dibujar la elipse que tiene por
ecuación:
4x2 + y2 �16x + 2y + 13 = 0
Solución:
La ecuación dada se puede escribir en las formas equivalentes:
(completación de cuadrado)
(factorización y simplificación)
(dividiendo por 4)
Esta última ecuación corresponde a la elipse cuyo centro es el punto C(2, -1),
semiejes;
a = 1 y b = 2. Como a < b, el eje focal es paralelo al eje y y tiene por ecuación x =
2 (ver fig. 6.5.10.).
Los vértices son los puntos V1(2, 1), V2(2, -3), V3(3, -1) y V4(1, -1).
Como
, se tiene que los focos están localizados en los puntos
y
.
fig. 6.5.10.
4. Propiedad Óptica de la Elipse
En geometría plana se demuestra el siguiente resultado: Si se tiene un triángulo
ABC y un punto D sobre BC (ver figura 6.5.11), entonces:
es Bisectriz del ángulo
.
Esta propiedad permite construir la normal y
por ende la tangente en un punto cualquiera
de la elipse.
Al unir el punto P1 de la elipse con F� y con
F, puede demostrarse que la bisectriz del
ángulo F�P1F
es la normal nn a la curva por P1 (fig.
6.5.12.).
fig. 6.5.11.
Esta propiedad se conoce como la propiedad óptica o focal de la elipse y tiene
interesantísimas aplicaciones:
fig. 6.5.12.
1) Considérese un rayo de luz que se enfoca desde un foco hacia un punto P1 de la
curva. Como nn es bisectriz del ángulo F�P1F, entonces, ángulo de incidencia =
ángulo de reflexión y por tanto el rayo se reflejará pasando por el otro foco. Este
hecho es utilizado en la construcción de conchas acústicas.
Supongamos que la elipse se hace rotar alrededor del eje x formando una superficie
de revolución e imaginemos un salón cuyos techos y paredes son la superficie
anterior. Cuando una persona habla desde un foco F, puede ser escuchada en el
otro foco a pesar de estar muy lejos del anterior y puede no ser audible en otros
puntos intermedios a causa de que las ondas de sonido chocan contra las paredes y
son reflejadas en el segundo foco y llegan a él en el mismo tiempo ya que ellas
viajan el mismo tiempo.
2) Estudiando una gran cantidad de datos experimentales, Kepler (1571 � 1630)
determinó empírica- mente los tres siguientes hechos sobre el movimiento de los
planetas conocidos como las leyes de Kepler:
1. La órbita de cada planeta es una elipse con el sol en uno de los focos.
2. El radio vector trazado desde el sol barre áreas iguales en tiempos
iguales.
3. Los cuadrados de los períodos de los planetas son proporcionales a los
cubos de los semiejes mayores de la órbita elíptica.
Newton (1642 � 1727) partiendo de estas tres leyes empíricas y utilizando
elementos del cálculo diferencial e integral pudo deducir la ley de gravitación
universal: "la fuerza que ejerce el sol sobre un planeta es una fuerza de atracción
radial e inversamente proporcional al cuadrado de la distancia entre los dos centros
del sol y del planeta y viene dada por
donde m: masa del planeta,
constante de gravitación universal".
M: masa del sol y
Fijadas la directriz, el foco F y la excentricidad
, sabemos que si llamamos p:
distancia foco - directriz, la ecuación de la elipse es
y
(1) donde
donde como se puede demostrar fácilmente que a
> b.
Ahora, cuando
, dejando fijos los demás elementos; directriz, foco y p, la
elipse se aproxima a una circunferencia y por tanto la órbita es cada vez mas
cercana a una circunferencia En efecto:
.
Si
y
y por tanto, a y b se acercan al
mismo valor y la ecuación (1) tiende a ser la ecuación de una circunferencia.
Esto puede verse también en el siguiente cuadro.
p=1
0.5
0.6666
0.57735
0.4
0.4762
0.4364
0.2
0.2083
0.2041
0.1
0.1010
0.1005
0.01
0.0100
0.0100
0.002
0.002
0.002
0.001
0.001
0.001
Muchos de los planetas incluyendo la tierra tienen órbitas que son
aproximadamente circulares:
Mercurio
0.21
Saturno
0.06
Venus
0.01
Urano
0.05
Tierra
0.02
Neptuno
0.01
Marte
0.09
Plutón
0.25
Júpiter
0.05
Uno de los objetos mas importantes del sistema solar es el cometa Halley que tiene
una excetrici- dad de
y una órbita de alrededor de 7 U.A. de ancho x 35
U.A. de largo (1 U.A.: 150 millones de kilómetros = semieje mayor de la órbita de
la tierra » distancia tierra � sol). El período de revolución de este cometa es de 76
años. Fue observado por el astrónomo Edmund Halley en 1682 el cual predijo que
volvería a aparecer en 1758. Asi efectivamente fue pero Halley no pudo ver
verificada su predicción ya que murió en 1742. Esta periodicidad de la órbita del
Halley fue uno de los sucesos mas convincentes a favor de la teoría de Gravitación
de Newton.
Hipérbola
Es el lugar geométrico de los puntos tales que el valor absoluto de la diferencia de sus
distancias a dos puntos fijos, llamados focos, es igual a una constante positiva igual a la
distancia entre los vértices.
Ecuaciones de la hipérbola
Ecuaciones en coordenadas cartesianas:
Ecuación de una hipérbola con centro en el origen de coordenadas
Ecuación de una hipérbola con centro en el punto
Ecuaciones en coordenadas polares
Dos hipérbolas y sus asíntotas.
Hipérbola abierta de derecha a izquierda:
Hipérbola abierta de arriba a abajo:
Hipérbola abierta de noreste a suroeste:
Hipérbola abierta de noroeste a sureste:
Ecuaciones paramétricas
Imagen de sección cónica.
Hipérbola abierta de derecha a izquierda:
Hipérbola abierta de arriba a abajo:
Véase también
•
•
•
•
•
Circunferencia
Parábola
Elipse
Sección cónica
Geometría analítica
Ejercicios
1. Los focos y los vértices de una hipérbola son los puntos: F(5, 0), F�(-5, 0), V1(4, 0) y
V2(-4, 0), respectivamente. Determine la ecuación de la hipérbola. Dibujar su gráfica e
indicar las asíntotas.
SOLUCIÓN
Como los focos están sobre el eje x, la ecuación de la hipérbola es de la
forma:
.
fig. 6.5.13.
En este caso: a = 4; c = 5, de donde
consecuencia, la ecuación de la hipérbola es:
(Ver fig. 6.5.13.) En
.
Ahora,
Luego, las ecuaciones de las asíntotas son las rectas:
, y,
2. Dada la hipérbola cuya ecuación viene dada por:
. Determine:
coordenadas de los focos, de los vértices, ecuaciones de las asíntotas. Trazar la gráfica.
SOLUCIÓN
La ecuación:
, puede escribirse en las formas equivalentes:
La última ecuación corresponde a una hipérbola cuyo eje focal coincide con el eje y
(fig. 6.5.14.)
fig. 6.5.14.
En este caso:
. Luego,
.
Con estos datos, se tiene: F(0, 4), F�(0, -4), V1(0, 3) y V2(0, -3).
Además de la ecuación:
, se deduce que las ecuaciones de las asíntotas
son las rectas de ecuación:
e
.
..
3. Una hipérbola cuyo centro es el punto C(2, 3), tiene sus focos sobre la recta y = 3.
Además, la distancia entre los focos es 10 unidades y la distancia entre sus vértices es 8
unidades. Trazar la gráfica y determine: coordenadas de los vértices, focos y ecuaciones de
las asíntotas.
SOLUCIÓN
Como la distancia entre los vértices es 8, se sigue que a = 4. Igualmente, como 2c = 10,
se sigue que c = 5 y por lo tanto b2 = c2 � a2 = 9. Asi que b = 3 (fig. 6.5.15.).
fig. 6.5.15.
Ahora, puesto que los focos están sobre la recta y = 3 (paralela al eje x), la ecuación de la
hipérbola pedida tiene la forma:
y y = 3. Esto es: F(7, 3) y F�(-3, 3).
Las coordenadas de los focos son:
y y = 3. Esto es, V1(6, 3) y
Igualmente, las coordenadas de los vértices son:
V2(-2, 3).
Además, de la ecuación:
que:
, se deduce
;y
son las ecuaciones de las asíntotas.
4. Dada la hipérbola, cuya ecuación en su forma general es: 3y2 � x2 + 4x � 6y � 13 =
0. Determine y grafique: centro, focos, vértices y
ecuaciones de las asíntotas.
SOLUCIÓN
La ecuación general, puede escribirse en las formas equivalentes:
Esta última ecuación corresponde a una hipérbola cuyo centro es el punto C(2, 1) y su eje
focal es una recta paralela al eje y que pasa por C(2, 1). En esta caso, x = 2 (fig. 6.5.16.)
fig. 6.5.16.
Además, a2 = 4, b2 = 12. Con lo cual:
Las coordenadas de los focos son: x = 2 e
.
. Esto es F(2, 5) y F�(2, -3).
Igualmente, las coordenadas de los vértices son: x = 2 e
-1).
Las ecuaciones de las asíntotas son las rectas:
. Esto es V1(2, 3) y V2(2,
, e,
.
5 .En el SISTEMA DE NAVEGACIÓN DE LARGO ALCANCE (LORAN, por sus siglas en inglés),
una estación principal de radio y una estación secundaria emiten señales que pueden ser
recibidas por un barco en el mar (ver fig. 6.5.17.). Aunque un barco recibe siempre las dos
señales, por lo regular se halla mas cerca de una de las dos estaciones y, por lo tanto, hay
cierta diferencia en las distancias que recorren las dos señales, lo cual se traduce en una
pequeña diferencia de tiempo entre las señales registradas. Mientras la diferencia de
tiempo permanezca constante, la diferencia de las dos distancias también será constante.
Si el barco sigue una ruta que mantenga fija la diferencia de tiempo, seguirá la trayectoria
de una hipérbola cuyos focos están localizados en las posiciones de las dos estaciones de
radio.
fig. 6.5.17.
Asi que para cada diferencia de tiempo se tiene como resultado una trayectoria hiperbólica
diferente, cada una llevando al barco a una posición distinta en la costa. Las cartas de
navegación muestran las diferentes rutas hiperbólicas correspondientes a diferencias de
tiempo distintas.
• Dos estaciones LORAN están separadas 250 millas a lo largo de una costa recta.
a) Un barco registra una diferencia de tiempo de 0.00086 seg. entre las señales LORAN.
Establezca un sistema de coordenadas rectangulares apropiado para determinar donde el
barco alcanzará la costa si continúa sobre la trayectoria de la hipérbola correspondiente a
esta diferencia de tiempo.
b) Si el barco debe entrar a un puerto localizado entre las dos estaciones a 25 millas desde
la estación principal, ¿qué diferencia de tiempo debe observar?.
c) Si el barco está a 80 millas de la costa cuando se obtiene la diferencia de tiempo
deseada, ¿cuál es su ubicación exacta? (Nota: la velocidad de cada señal de radio es de
186.000 millas/seg.).
..
SOLUCIÓN
a. Se puede establecer un sistema de coordenadas rectangulares de tal forma que las dos
estaciones estén sobre el eje x y el origen de coordenadas en la mitad del camino entre
ellas (Ver fig. 6.5.18.).
fig. 6.5.18.
Como la diferencia de tiempo constante de las señales desde cada estación implica una
diferencia constante en la distancia del barco a cada una de las estaciones, se deduce
entonces que el barco está localizado sobre una hipérbola cuyos focos son las estaciones e
radio.
Ahora, dif. dist. = Veloc. (dif. de tiempos)= 186.000 x 0.00086 = 160 millas.
Esto indique que 2a = 160 (recordar la definición de la hipérbola) y de aquí a = 80, lo que
indica que uno de los vértices de la hipérbola está en el punto V1(80, 0). Ahora, como uno
de los focos está en el punto F(125, 0) se deduce entonces que el barco siguiendo la
trayectoria hiperbólica alcanzará la costa a 125 � 80 = 45 millas de la estación principal.
b. Si el barco desea entrar sobre la costa a 25 millas de la estación principal, esto indica
que debe seguir una trayectoria hiperbólica cuyo vértice es el punto V(100, 0). Asi que 2a
= 200 (diferencia constante entre las distancias del barco a cada estación).
De esta forma:
.
c. Para encontrar la ubicación exacta del barco, se necesita determinar la ecuación de la
hipérbola cuyo vértice es V(100, 0) y uno de sus focos es F(125, 0).
Asi que a = 100, c = 125. Con lo cual, b2 = c2 � a2 = 5625.
De esta forma, la ecuación de la hipérbola viene dada por:
Como el barco está a 80 millas sobre la costa, quiere decir que está en el punto (x, 80)
sobre la hipérbola. En consecuencia,
, de donde x = 146.
Por lo tanto, la ubicación exacta del barco es sobre la hipérbola en el punto P(146, 80).