Cuadro sintético - Ciencia en la UTN

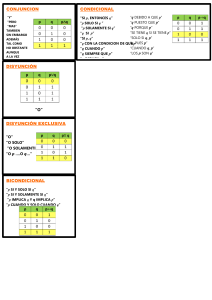
Universidad Tecnológica Nacional
Facultad Regional Mendoza
Metodología de la Investigación
Prof. Esp. Flavio Hernán Teruel
Cuadro sintético
Tema:
•
El método de deducción: reglas lógicas de inferencia y reglas de reemplazo de
equivalentes
Lectura:
•
Copi, Irving (1979), "El método de deducción", en su: Lógica simbólica, México,
Compañía Editorial Continental, pp. 49-86.
§1
Reglas lógicas de inferencia
Las reglas lógicas son formas de razonamiento válidas y elementales que al sustituir
sus variables por constantes dan lugar a razonamientos válidos. Con la ayuda de estas reglas
lógicas elementales es posible demostrar la validez de razonamientos complejos. En su
formulación se utilizan las letras "A", "B", "C", etc., denominadas variables metalógicas, para
indicar que cada una de ellas puede designar una proposición atómica o molecular tan compleja
como se quiera. Algunas de las más importantes reglas lógicas son las siguientes:
Reglas de inferencia
Modus Ponens (M.P.)
Dilema Destructivo (D.D.)
Silogismo Disyuntivo (S.D.)
p⊃q
p
∴q
p⊃q
r⊃s
~q∨~s
∴~p∨~r
Modus Tollens (M.T.)
Dilema Constructivo (D.C.)
p⊃q
~q
∴~p
p⊃q
r⊃s
p∨r
∴q∨s
Silogismo Hipotético (S.H.)
Conjunción (Conj.)
Adición (Ad.)
p⊃q
q⊃r
∴p⊃r
p
q
∴p⋅q
p
∴p∨q
p∨q
~p
∴q
p∨q
~q
∴p
Simplificación (Simpl.)
p⋅q
∴p
p⋅q
∴q
Estas nueve reglas de inferencia son formas válidas elementales de argumentos cuya
validez fácilmente se establece mediante tablas de verdad. Pueden usarse para construir
pruebas formales de validez para una amplia clase de argumentos más complicados. Los
nombres de la lista son estándar en su mayor parte, y el uso de sus abreviaciones permite
presentar las pruebas formales con un mínimo de escritura.
§2
Reglas de reemplazo de equivalentes
Reglas de Reemplazo
Doble negación (D.N.)
p≡~~p
Transposición (Trans.)
(p⊃q)≡(~q⊃~p)
Conmutación (Conm.)
Asociación (Asoc.)
de la conjunción
(p⋅q)≡(q⋅p)
de la disyunción
(p∨q)≡(q∨p)
del bicondicional
(p≡q)≡(q≡p)
de la conjunción
[p⋅(q⋅r)]≡[(p⋅q)⋅r]
de la disyunción
[ p ∨ ( q ∨ r) ] ≡ [ ( p ∨ q ) ∨ r ]
del bicondicional
[p≡(q≡r)]≡[(p≡q)≡r]
de la conjunción respecto de la
disyunción
de la disyunción respecto de la
conjunción
del condicional respecto de la
conjunción
del condicional respecto de la
disyunción
Distribución (Dist.)
Teoremas de De Morgan (De
M.)
[p∨(q⋅r)]≡[(p∨q)⋅(p∨r)]
[p⊃(q⋅r)]≡[(p⊃q)⋅(p⊃r)]
[p⊃(q∨r)]≡[(p⊃q)∨ (p⊃r)]
conjunción a disyunción
~(p⋅q)≡(~p∨~q)
disyunción a conjunción
~ ( p ∨ q ) ≡ (~ p ⋅ ~ q)
Definición del condicional o implicación material (Impl.)
Definición del bicondicional o equivalencia material (Equiv.)
(p⊃q)≡(~p∨q)
(p⊃q)≡ ~(p⋅~q)
(p≡q)≡[(p⊃q)⋅(q⊃p)
(p≡q)≡[(p⋅q)∨(~p⋅~q)]
[(p⋅q)⊃r]≡[p⊃(q⊃r)]
Exportación (Exp.)
Idempotencia o tautología (Taut.)
Expansión booleana (Bool.)
Absorción (Abs.)
[p⋅(q∨r)]≡[(p⋅q)∨(p⋅r)]
p≡(p⋅p)
p≡(p∨p)
p≡p⋅(q∨~q)
p≡p∨(q⋅~q)
p≡[p⋅(p∨q)]
p≡[p∨(p⋅q)]
La Regla de Reemplazo autoriza que expresiones lógicamente equivalentes especificadas se
reemplacen entre sí donde ocurran, aun en donde no constituyan renglones enteros de una
demostración. Pero las nueve primeras Reglas de Inferencia sólo pueden usarse tomando como
premisas renglones enteros de una demostración.
§3
Método demostrativo o prueba formal de validez
El método demostrativo es un procedimiento apto para demostrar la validez de un
razonamiento dado. El método consta de los siguientes pasos:
1. Dado un razonamiento, se abstrae su forma lógica.
2. Dejando de lado la conclusión, y por aplicación de las reglas lógicas a las premisas, se
van derivando formas proposicionales hasta llegar a la conclusión: si esto se logra, el razonamiento
es válido.
Supongamos un razonamiento cuya forma es la siguiente:
1 p⊃q
2 q⊃r
3 ~r/∴~p
4 p⊃r
de 1 y 2 por SH
5 ~p
de 4 y 3 por MT
Como se ha logrado llegar a la conclusión partiendo de las premisas y efectuando
transformaciones legitimadas por las reglas lógicas, el razonamiento es válido.
Como el método demostrativo no es un método mecánico se puede, en ocasiones, seguir
diversos caminos de deducción. Por ejemplo, en el caso anterior se pudo haber procedido de la
siguiente manera:
4 ~q
de 2 y 3 por MT
5 ~p
de 1 y 4 por MT
Las demostraciones anteriores constituyen ejemplos de lo que se denomina una prueba
formal de validez, es decir, "[...] una sucesión de enunciados, cada uno de los cuales es una premisa
de ese argumento o se sigue de los precedentes por un argumento válido elemental, y tal que el
último enunciado de la secuencia es la conclusión del argumento cuya validez se está demostrando."
***