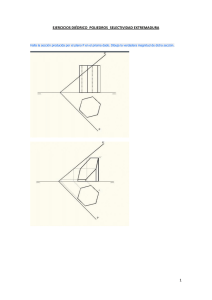
PLANO HORIZONTAL (PH)

SISTEMA DIEDRICO
Del espacio al plano
Foco
P
PROYECTAR: Cuando un rayo de proyección procedente de
un foco incide en un punto P, la “sombra” de ese punto sobre
un plano de proyección P´, será la proyección de P. El rayo
proyectante será una recta de proyección. La intersección de la
recta de proyección que pasa por el punto e intersecciona con
un plano será la proyección.
Diferentes tipos de proyección:
-Proyección oblicua.
P
-Proyección ortogonal.
-Proyección cónica.
-Proyección cilíndria.
P´
-Proyección cilíndrica ortogonal.
A
B
B´
Proyección Oblicua
B
A´
Proyección Cónica
A
B´ A´
Proyección Cilíndrica
Oblicua
PLANOS DE PROYECCIÓN: Son los planos donde se
proyecta: El Plano Vertical (PV) y el Plano Horizontal (PH)
se cortan entre sí perpendicularmente.
Esta intersección se llama Línea de Tierra (LT).
Los dos planos dividen el espacio en 4 cuadrantes iguales. El
espectador solo ve lo que ocurre en el 1er. Cuadrante .
recta proyectante
P´Proyección
P´
Plano proyectante
A
B
P
P´
B´
A´
Proyección Oblicua
de una recta
Proyección Ortogonal (90º)
A
B
B´ A´
Proyección Cilíndrica
Ortogonal.
V)
(P
CTI AL
VER
O
PLAN
Plano Vertical (PV)
(
ETI RRA
lt)
DE
A
E
Línea
de Tierra (LT)
LIN
PLANOHORIZONTAL(PH)
Plano Horizontal (PH)
ABATIMIEMTO: El PH se abate sobre el PV mediante un
giro que tiene como eje la LT. A este eje se le llama Charnela.
En el sistema diédrico por tanto representamos las
características de los objetos en el espacio (3 dimensiones) en
un solo plano (2 dimensiones).
Abatimiento de los planos de proyección
L
A2
(PV)
A
z
Cota
PROYECCIONES DE PUNTOS: Los puntos se nombran
con letras mayúsculas: A,B, C, P, M, N...
En el espacio son solamente las letras, en el sistema diédrico
son sus representaciones como proyecciones horizontal y
vertical: A1 y A2.
A1 la proyección en el plano horizontal y A2 en el plano
vertical. (Si existe un tercer plano de proyección como por
ejemplo el de perfil sería A3).
X
ia
nc Alejamiento
0 Dista
A1
(PH)
A (20, 10, 30) Coordenadas del punto
A2
A2
Cota (30)
La distancia del punto al plano vertical se llama
ALEJAMIENTO y la distancia al plano horizontal COTA
(altura).
Por lo tanto un punto representado en el sistema diédrico se
puede colocar exactamente en su posición espacial según las
coordenadas de altura (Cota) y distancia (Alejamiento)
A (X, Y) A( alejamiento X y cota Y)
Para saber qué posición tiene un punto en el espacio (3D) se
toma una tercera referencia, llamada Distancia, y es la medida
con respecto a un punto 0 en la Línea de Tierra.
:
Y
Distancia 20
0
RESUMEN PROYECCION DE UN PUNTO
A2
A1
A (X, Y, Z)
A2
A2
A2
A
Alejamiento (10)
A1
X=Distancia
y= Alejamiento
z = Cota.
A1
A1
A1
A1
A1, A2 y A3 es la representación
en el plano de el punto A en el
espacio (3D)
TERCERA PROYECCIÓN DE UN PUNTO (VISTA DE PERFIL)
A2
A2
A3
A
A3
A2
A1
A3
A3
A2
A1
A1
A1
PROYECCIÓN DE UN RECTA (UNIMOS LAS PROYECCIONES DE DOS PUNTOS)
A2
r2
A2
r
r2
B2
A2
A
r2
r1
B2
r2
B2
B2
B
B1
A2
A1
B1
r1
A1
Las coordenadas de una recta están definidas por las coordenadas
de dos puntos. Por ejem. r = A (20, 10, 30) y B (5, 5, 10)
B1
r1 A 1
B1
r1
A1
sistema diédrico. las vistas
Para representar en el plano las tres dimensiones de un objeto tridimensional, se utilizan las proyecciones diédricas
horizontal, vertical y si es necesario, la de perfil de dicho objeto. Estas proyecciones de todos los vértices, aristas
y caras del objeto en los tres planos de proyección se denominas vistas. La proyección horizontal se llama PLANTA,
la proyección vertical: ALZADO y la tercera proyección PERFIL.
SISTEMA EUROPEO: Es el denominado para representar
los objetos con las proyecciones de esta manera.
ALZADO
PERFIL IZQUIERDO
PLANTA
ejemplo de represetación de las vistas de una pieza
PERFIL derecho
ALZADO
Hay que tener en cuenta la posición
en la que nos encontramos para ver
la pieza y cual es el alzado.
Cuidado con el perfil. Observar bien
en qué lugar está situado.
TODOS LOS PUNTOS Y VISTAS TIENEN
QUE COINCIDIR EN SUS REPRESENTACIONES HORIZONTALES, VERTICALES Y
DE PERFIL.
PLANTA
ejemplo de represetación de las vistas
de una silla realizada por alumnos.