Fórmula

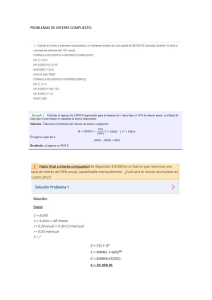
MATEMATICAS APLICADAS
CLASE 2
INTERES SIMPLE
Desventajas:
1. Su aplicación es limitada.
2. No considera el valor del dinero en el tiempo.
3. No capitaliza los intereses no pagados en los
periodos anteriores, por lo que pierden poder
adquisitivo.
INTERES SIMPLE
PROBLEMAS
1.
2.
3.
4.
5.
Un préstamo de $4’500,000.00, ¿cuánto tardará en producir en intereses
una cantidad de $253,130.00 de interés simple, si la tasa es del 45%?
¿En cuánto tiempo se duplicará una cierta cantidad de dinero si se invierte
al 40% de interés simple?
Un comerciante de llantas consigue un crédito a 25 días de plazo a una tasa
del 3% mensual, si el monto del crédito es de $3’500,000.00, ¿cuánto interés
pagara?
Una fabricante de calzado compra una máquina, la cual tiene un precio de
contado de $1’765,000.00. Si da un anticipo de $500,000.00 y el pago final a
3 meses, ¿cuánto pagará a los 3 meses si acepta pagar una tasa de interés
del 42% sobre el saldo?
Un cliente invierte en BB una cantidad de $5’500,000.00 a un plazo de 28
días. Si al vencimiento recibió la cantidad de $5’620,000.00, a) ¿qué
rendimiento (interés) obtuvo?, b) ¿qué tasa de interés anual ganó?
VALOR FUTURO A INTERES SIMPLE
Es la cantidad que una inversión crecerá después de
ganar intereses.
Fórmula:
VF ó FV ó F = PV ( 1 + i )
VF – valor futuro
PV – valor presente
i – tasa interés
VALOR FUTURO A INTERES SIMPLE
Ejemplo
Encontrar el monto de una inversión de $200,000.00 en un
periodo de 5 años a una tasa del 25% anual
Fórmula:
VF = PV ( 1 + i n) = 200,000 (1+0.25*5)= $450,000.00
VF – ?
PV – $200,000.00
i – 25%
n – 5 años
VALOR PRESENTE A INTERES SIMPLE
Es la cantidad que se necesitaría invertir hoy para
que sea igual que el monto futuro
Fórmula:
P ó PV= VF
(1 + in)
VF – valor futuro
PV – valor presente
i – tasa interés
n - periodos
VALOR PRESENTE A INTERES SIMPLE
Ejemplo
Se desea tener una suma de $3’500,000.00 a 2.5 años, si se tiene una
tasa del 2.8% mensual. ¿Cuál debe ser el valor inicial de la
inversión?
Fórmula:
P ó PV=
VF =
(1 + in)
PV - ?
VF – $3’500,000.00
i – 2.8%
n – 2.5 años = 30 meses
3500000
= $1’902,173.91
(1 + (0.028*30))
Otras fórmulas…
F
i= P
F
n= P
1
n
1
i
Ejemplo
BB ofrece un préstamo de $2’000,000.00, cobra después de 8 meses la suma de
$2’400,000.00. ¿Qué tasa de interés mensual simple cobró?
F
i= P
1
=
n
2400000
2000000
8
1
= 0.025 ó 2.5%
Ejemplo
¿En cuánto tiempo se acumularían $8’000,000.00 si se depositan hoy $2’500,000.00 en
una inversión que pagar el 3% de interés simple mensual?
F
n= P
1
i
=
8000000
2500000
0.03
1
= 73.3 meses
VALOR PRESENTE Y VALOR FUTURO INTERES
SIMPLE
PROBLEMAS
1.
2.
3.
4.
5.
6.
Se recibe un préstamo por $2’000,000.00 al 30% de interés simple a 10 meses,
¿cuál será el monto del préstamo al término del plazo?
Un cliente recibe un préstamo de $918,300.00 a 25 días, si le aplican una tasa de
interés del 3% mensual, ¿Cuánto pagará por el crédito?
Encontrar el valor presente de $3’800,000.00 que vence dentro 7 meses a una
tasa de interés del 25%.
Una persona compra un automóvil en $157,000.00 el 1° de enero, si la vende el
1°de julio del siguiente año en $215,000.00. ¿Fue conveniente como inversión la
operación realizada si la tasa del interés era del 30%?
¿En qué tiempo se tendría la cantidad de $540,000.00 si se depositarán hoy
$300,000.00 en un fondo que paga el 3.2% de interés simple mensual?
¿Cuál es el precio de contado de un automóvil que se paga dando un enganche
del 25% del precio de contado y se firma un pagaré a 3 meses por $120,000.00
que incluye una tasa del 24% anual?
VALOR PRESENTE Y VALOR FUTURO INTERES
SIMPLE
PROBLEMAS
7.
Calcule el rendimiento de un bono que paga una tasa del 5% mensual a un plazo
de 1 año. Si al final del tiempo se acumula una cantidad de $600,000.00
8. Una persona desea saber cuánto tiempo tiene que esperar para recibir una
cantidad de $3’500,000.00, si invirtió $1’000,000.00 a una tasa mensual del 10%
9. Una empresa desea invertir un proyecto que le va dar un rendimiento de
$10’000,000.00 a un plazo de 9 años con una inversión de 6’000,000.00. Por otro
lado le ofrecen invertir la misma cantidad a una tasa de rendimiento del 8% en
otro producto. ¿Qué le conviene más?
10. Un deudor que pidió un crédito inicial por $800,000.00 a un plazo de 14 meses.
Si al final del plazo tiene que pagar una cantidad de $1’100,000.00, ¿qué tasa
anual le están cobrando?
11. Un cliente está analizando invertir en un bono que ofrece una tasa anual del
40%, si invierte $500,000.00 y al final del tiempo recibirá un rendimiento de
$250,000.00, ¿Cuántos meses debe esperar para recibir dicho rendimiento?