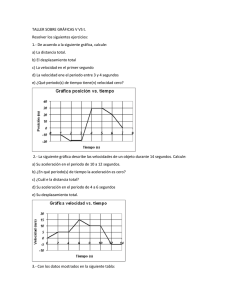
3Resuelva el siguiente ejercicio en base a la tabla

CINEMATICA
1The position vector locating the point P(5,12) relative to the origin is
A) 12
iˆ + 5 ĵ
B) –5
iˆ – 12 ĵ
C) 5
iˆ + 12 ĵ
D) 13
iˆ + 13 ĵ
E) 13
iˆ – 13 ĵ
Vector de posición, componentes cartesianas, ángulo con el eje x, vector unitario
2If an object is moving west, its acceleration
A) is north.
B) is east.
C) is west.
D) is south.
E) may be any direction.
Aceleración =d velocidad/d tiempo, se necesita información de la velocidad en dos tiempos
A car is at position (x1, y1) = (4 m, 5 m) at time t1 = 1 s. If 10 seconds later the car moving in a
straight line is at position (x2, y2) = (204 m, 305 m), calculate the magnitude of the average
velocity during this interval.
Vector desplazamiento, velocidad media en un intervalo de tiempo
A) 36.1 m/s
B) 32.8 m/s
C) 36.7 m/s
D) 50.0 m/s
E) 40.1 m/s
Ans: A
Interpretar
3Resuelva el siguiente ejercicio en base a la tabla mostrada:
movimiento en una dimensión
Tiempo /s Posición /m
0
0
5
100
10
300
15
300
20
400
25
500
35
0
a) Trace una gráfica posición vs tiempo
b) Calcule la longitud total de la trayectoria (espacio recorrido)
c) Calcule el desplazamiento total
d) Calcule la velocidad media en los primeros 5 segundos
e) Calcule la velocidad media en el periodo de 15 a 25 segundos
a) gráfica posición vs. tiempo
b) Calcule el espacio recorrido
Se obtiene sumando todos los desplazamientos, ya que la
distancia es una cantidad escalar y no tiene dirección por esta
causa se suman numéricamente todos los tramos.
100+200+0+100+100+500 = 1000 m.
c) Calcule el desplazamiento total
0 ya que el objeto salió y llegó al mismo lugar.
c)Calcule la velocidad media en los primeros 5 segundos.
Esto se calcula con la pendiente de la gráfica , la cual nos da la
velocidad, utilizando la siguiente fórmula:
V = d2 - d1 = 100 - 0 = 20 m/s
t2 – t1
5-0
e) Calcule la velocidad media en el periodo de 15 a 25
segundos.
V = d2 - d1 = 500 - 300 = 20 m/s
t2 – t1
25 - 15
Resolver los siguientes ejercicios
4 En base a los datos mostrados en la siguiente tabla:
movimiento en una dimensión
Tiempo/s
0
2
3
4
5
6
7
8
Posición/m
-40
-25
-25
-20
0
25
25
15
Construya la grafica x(t) y calcule:
a) El desplazamiento total.
b) El espacio recorrido
c) Los periodos de velocidad constante.
d) La velocidad en los primeros dos segundos
e) La velocidad de 7 a 8 segundos
5De acuerdo con la gráfica
mostrada:
a) Calcule la distancia total.
b) Calcule el desplazamiento total.
c) La velocidad en el periodo de 4 a 6 segundos.
d) La velocidad en los dos primeros segundos.
e) La velocidad en el periodo de 10 a 12 segundos
6De acuerdo con la gráfica
mostrada, indique:
a) La distancia total recorrida.
b) El desplazamiento total
c) La velocidad en los primeros 5 segundos.
d) La velocidad en el periodo de 20 a 25 s
73x-2y =8; y-x=2
Primero gráficamente; luego resolver el sistema: x=12, y=14
La relación xy=4 es lineal?
Movimiento uniforme: x=vt, v=cte, ¿ es lineal x con t? dibuja
X aumenta v metros cada segundo
La aceleración es cero
Caída de una piedra : x =(1/2 )gt2
¿es lineal x con t? dibuja
La aceleración es constante g=cte distinta de cero ¿qué tipo de
movimiento?
V aumenta g m/s cada segundo: v = gt ¿es lineal v con t? dibuja
8Desde una altura de 9 m se lanza un cuerpo hacia arriba con
una v inicial de 12 m/s. Determina: su altura, su velocidad y su
aceleración al cabo de 1 y 2 segundos de ser lanzado. Respuestas: 16
m y 13 m, 2 m/s y -8 m/s. Determina cuánto tarda en llegar al suelo:
3 s. Determina la altura máxima que alcanza: 16.2 m.
Movimiento circular
9Un punto A de una rueda que gira según un movimiento circular
uniforme, está situado a 20 cm del eje de rotación y tiene una
velocidad lineal de 8 m/s. Calcula la velocidad lineal de otro punto B a
30 cm del eje. ¿Cuántas vueltas da la rueda en 10 s? 12 m/s ; 63.7
vueltas