1 1 D F p LR V Radio vector a b 07y10x6-y2 x2 =+ + + 0 53y8

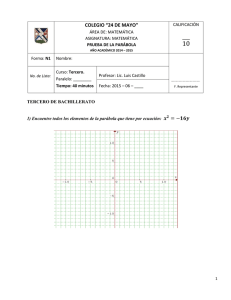
Facultad de Matemáticas – UADY
Departamento de Matemática Educativa
Curso de Nivelación en Matemáticas
Módulo 3: Geometría Analítica
Ejercicios
1) Determinar si cada una de las siguientes ecuaciones representa o no una circunferencia. Si la
respuesta es afirmativa, hallar su centro y su radio.
a) 2 x 2 + 2 y 2 - 6 x + 10 y + 7 = 0
b)
4 x 2 + 4 y 2 + 28 x - 8 y + 53 = 0
c)
16 x 2 + 16 y 2 - 64 x + 8 y + 77 = 0
2) Determina
2
si
las
circunferencias
4 x 2 + 4 y 2 - 16 x + 12 y + 13 = 0
y
2
12 x + 12 y - 48 x + 36 y + 55 = 0 son concéntricas.
3) Hallar la ecuación de la circunferencia cuyo centro está sobre el eje X y que pasa por los
puntos A(1, 3) y B(4, 6).
4) Hallar la ecuación de la circunferencia que pasa por los puntos (-1, -4), (2, –1) y cuyo centro
está sobre la recta 4 x + 7 y + 5 = 0 .
5) Hallar la ecuación de la circunferencia que pasa por el punto (5, 9) y que es tangente a la
recta x + 2 y - 3 = 0 en el punto (1,1).
6) Una circunferencia de radio 5 pasa por los puntos (0, 2) y (7, 3). Hállese su ecuación. (Se tiene
comos ecuaciones como solución).
7) Hallar la ecuación de la circunferencia que pasa por los puntos (2, -2), (-2, -4) y (4, 2).
8) Hallar la ecuación de la circunferencia circunscrita al triángulo cuyos lados están determinados
por las intersecciones de las rectas x - y + 2 = 0 , 2 x + 3 y - 1 = 0 , y 4 x + y - 17 = 0 .
4.2.
Parábola
Definición. La parábola es el lugar geométrico de los puntos del plano que equidistan de un punto
fijo y de una recta fija del mismo plano. El punto fijo se llama Foco de la parábola y la recta fija es
su directriz.
Si la grafica de la parábola fuera la figura de abajo, se identificarían los siguientes elementos:
Elementos de la parábola
D
Radio vector
a
1
p
V
LR
1
x
F
b
Octubre, 2009
Foco: Es el punto fijo F.
Eje Focal: Es la recta que pasa por el Foco y es
perpendicular a la Directriz. Representa el eje de
simetría de la parábola. También se conoce
como el eje de la parábola.
Directriz: Es la recta perpendicular al eje focal. Es
la recta fija D.
Vértice V: Punto de intersección de la curva con
su eje focal.
Radio vector: segmento que une un punto
cualquiera de la parábola con el foco.
Parámetro: Es la distancia del vértice al foco de
la parábola, se designa por la letra P.
Lado recto: Es la secante que pasa por el foco y
es perpendicular al eje de la parábola. La longitud
del lado recto se designa como L.L.R = |4p|
Excentricidad: e = 1
8
Facultad de Matemáticas – UADY
Departamento de Matemática Educativa
Curso de Nivelación en Matemáticas
Módulo 3: Geometría Analítica
Ecuaciones ordinarias
Parábola
con
vértice en
el origen
Horizontal Que se extiende hacia la
derecha
y 2 = 4 px
Foco: F(p, 0)
Directriz: x = -p
O
Que se extiende hacia la
izquierda
y 2 = -4 px
Foco: F(-p, 0)
Directriz: x = p
Que se extiende hacia arriba
Vertical
x 2 = 4 py
Foco: F(0,p)
Directriz: y = -p
Que se extiende hacia abajo
x 2 = -4 py
Foco: F(0,-p)
Directriz: y = p
Parábola
Horizontal Que se extiende hacia la
con
derecha
Vértice en
( y - k )2 = 4 p( x - h )
(h, k)
Foco: F(h+p, k)
Directriz: x = h-p
Octubre, 2009
9
Facultad de Matemáticas – UADY
Departamento de Matemática Educativa
Curso de Nivelación en Matemáticas
Módulo 3: Geometría Analítica
Que se extiende hacia la
izquierda
( y - k )2 = -4 p( x - h )
Foco: F(h-p, k)
Directriz: x = h+p
Vertical
Que se extiende hacia arriba
( x - h )2 = 4 p( y - k )
Foco: F(h, k+p)
Directriz: y = k -p
Que se extiende hacia abajo
( x - h )2 = -4 p( y - k )
Foco: F(h, k-p)
Directriz: y = k+p
Ecuación general de la parábola
Toda ecuación de la parábola vertical se puede expresar por medio de una ecuación del tipo:
Ax 2 + Dx + Ey + F = 0
con A, D, E y F constantes.
Toda ecuación de la parábola horizontal se puede expresar por medio de una ecuación del tipo:
Cy 2 + Dx + Ey + F = 0
con C , D, E y F constantes.
Octubre, 2009
10
Facultad de Matemáticas – UADY
Departamento de Matemática Educativa
Curso de Nivelación en Matemáticas
Módulo 3: Geometría Analítica
Ejercicios
1) Determina la ecuación de la parábola de vértice en el origen y foco el punto (3,0).
2) Hallar la ecuación de la parábola de vértice en el origen y directriz la recta x + 5 = 0.
3) Una parábola cuyo vértice está en el origen y cuyo eje focal coincide con el eje X pasa por el
punto (-2,4). Hallar la ecuación de la parábola, las coordenadas del foco, la ecuación de la
directriz y la longitud de su lado recto.
4) Hallar la ecuación de la parábola cuyo vértice y foco son los puntos (-4,3) y (-1,3)
respectivamente. Hallar también las ecuaciones de su directriz y su eje focal.
5) Hallar la ecuación de la parábola cuyo vértice y foco son los puntos (3,3) y (3,1)
respectivamente.
6) La directriz de una parábola es la recta y – 1 = 0 y su foco es el punto (-4,3). Hallar la ecuación
de la parábola.
En los ejercicios 7 y 8, reduzca la ecuación de la parábola en su forma ordinaria y halle las
coordenadas del vértice y del foco, las ecuaciones de la directriz y eje focal.
7) 4y2 – 48x – 20y = 71
8) 9x2 + 24x + 72y + 16 = 0
9) Hallar la ecuación de la parábola cuyo eje es paralelo al eje X y que pasa por los tres puntos
(0,0), (8,-4) y (3,1).
10) Hallar la ecuación de la parábola de vértice el punto (4,-1), con eje focal sobre la recta y + 1 =
0 y que pasa por el punto (3,-3).
4.3.
Elipse
Definición. La elipse es el lugar geométrico de un punto P(x, y) que se mueve sobre un plano de
manera tal que la suma de sus distancias a dos puntos fijos es siempre constante. Los puntos fijos
se llaman focos.
Elementos de la elipse
LR
Longitud del eje mayor (V1V2) = 2a
Longitud del eje menor (B1B2) = 2b
Distancia entre los focos (F1F2) = 2c
Se cumple la siguiente relación entre
los parámetros a, b y c:
c 2 = a2 − b2
2b 2
Longitud del lado recto (L.R.) = a
c
e = <1
a
Excentricidad.
Octubre, 2009
11