Circuitos Serie y Paralelo en Paralelo en AC.

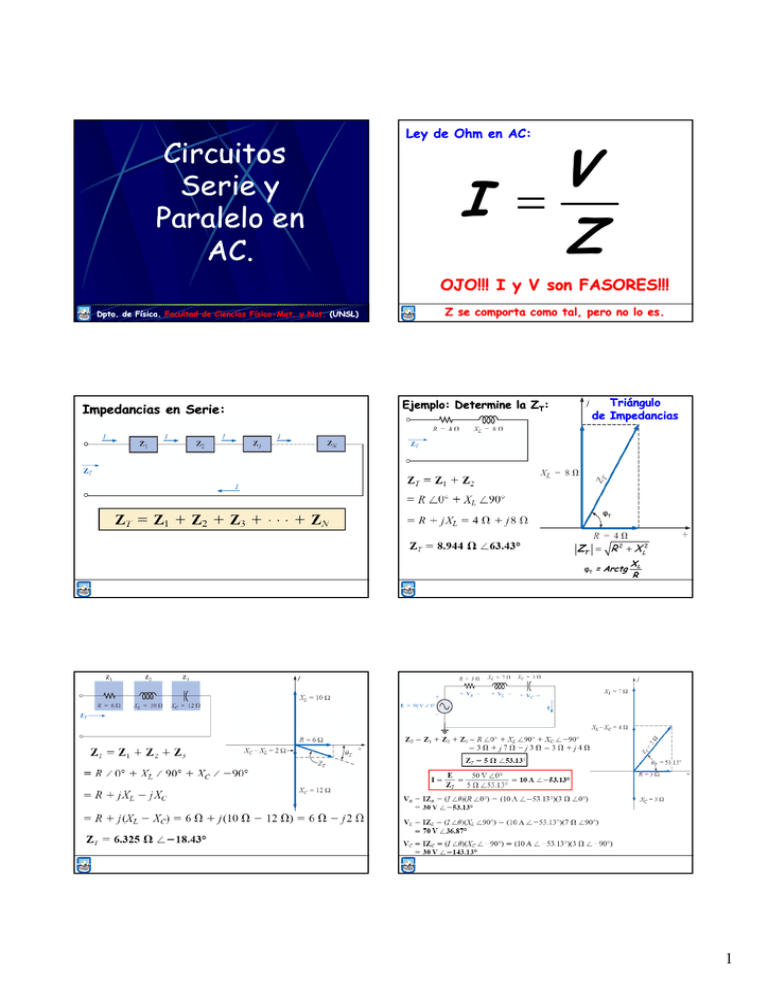
Circuitos
Serie y
Paralelo en
AC..
AC
Ley de Ohm en AC:
V
I =
Z
OJO!!! I y V son FASORES!!!
Dpto. de Física. Facultad de Ciencias FísicoFísico-Mat. y Nat. (UNSL)
Impedancias en Serie:
Z se comporta como tal, pero no lo es.
Ejemplo: Determine la ZT:
Triángulo
de Impedancias
φT
ZT = R 2 + XL2
φT = Arctg
XL
R
1
V = 50∠0°
I = 10∠ − 53.13°
VR = 30∠ − 53.13°
VL = 70∠36.87°
VC = 30∠ − 143.13°
Diagrama de
Fase
Circuitos Paralelos en AC - Admitancia (Y)
Z1
Z2
Z3
1
1
1
1
1
=
+
+
....
ZT Z1 Z2 Z3 ZN
YT = Y1+Y2+Y3+…+YN
ZN
Z=1/
=1/Y
Y
Conductancia y Susceptancia:
Triángulo de Admitancias:
2
Ejemplo:
Circuitos SerieSerie-Paralelo
en AC.
ZL
Z1
-80.54
ZC
Z2
ZT
Potencia en
AC..
AC
IC
IS
IL = 39.48∟
39.48∟-99.46º
99.46º
VL = 118.44∟
118 44∟
118.44
44∟-9.46º
9 46º
9.46
46º
VR
VC
IL
VL
Dpto. de Física. Facultad de Ciencias FísicoFísico-Mat. y Nat. (USL)
3
Potencia en un circuito resistivo
p(t)=
(t)=vv(t)
(t)ii(t)
Factor de Potencia: FP=cos(
=cos(θ
θ)
Potencia instantánea
θ: Diferencia de Fase
Potencia en un circuito Inductivo
Potencia Promedio (Real)
Potencia en un circuito Capacitivo
Potencia Reactiva
Para el Inductor:
4
Triángulo de Potencias:
Potencia Reactiva
Para el Capacitor:
Las Potencias Reactivas y Real se relacionan:
S = P + Q
S =VI
p
[VA]
[ ]
S es la Potencia Aparente.
S = P + j(QL-QC)
S =VI*
xI2
Lean el Libro!
5